基于博弈论的养老服务床位需求的预测与运营模式研究
罗媛 张力夫 刘斌洁


摘 要:随着老龄化社会问题突出,解决养老服务问题迫在眉睫。对养老服务问题分析,建立企业、需求者双方博弈模型。利用纯策略均衡分析得六种策略组合,通过企业策略和养老服务需求者策略参数大小关系得总收益最大化策略:企业进入养老产业和老人选择机构养老。提供给企业商机,达到利益最大化措施有:1.尽早进入市场,夺取市场份额。2.合理采购硬件设备,利用空窗期减低运营成本。
关键词:养老床位;博弈模型;纯策略均衡分析;多元回归模型
引言
老龄化人口增多,但机构养老的服务床位供给远远不满足社会需求,政府和各方面都在努力解决。因此,从政府角度,合理估计养老服务中床位的需求,制定合理的养老服务床位发展规划,是构建和谐、幸福社会的重要部分。从企业角度,养老服务床位的增加也为企业提供了一个“商机”。
1 模型建立
设博弈参与者为:r={企业;养老服务需求者},设博弈参与者战略空间为:S1={进入养老行业,不进入养老行业},S2={社区养老,居家养老,机构养老}。企业应对策略:积极参与和消极退出。积极参与概率X1(0
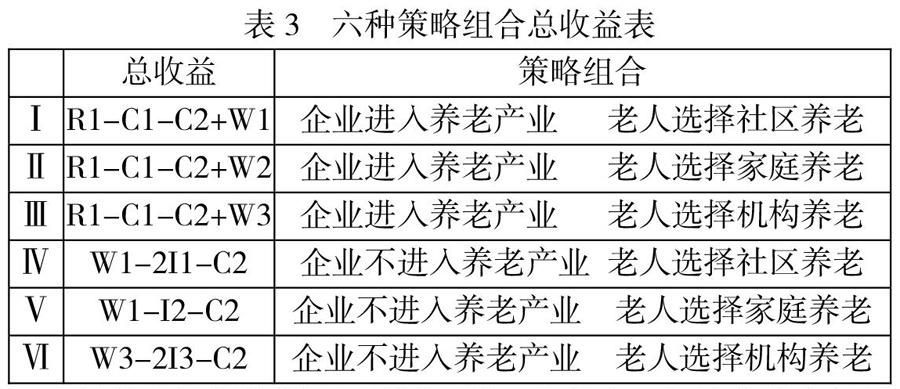
根据老年需求者三种策略,设社区养老概率Y1(0 将企业策略和养老需求者策略进行排列组合得到六种策略组合:企业进入养老产业老人选择社区养老;企业进入养老产业老人选择家庭养老;企业进入养老产业老人选择机构养老;企业不进入养老产业老人选择社区养老;企业不进入养老产业老人选择家庭养老;企业不进入养老产业老人选择机构养老。 根据六种策略组合确定企业的收益函数,老人的收益函数分别为:u1=u1{s1,s2···sd1}d1=2;u2={s1,s2···sd2}d2=3。那总收益函数为两者之和:u=u1+u2,d=d1·d2。最终参考文献[2]建立标准式博弈模型:G={S1,S2;u1,u2}。其中博弈模型的解纳什均衡为:在G中,收益之和最大时对应的策略组合即是博弈的纳什均衡。 2 模型求解 根据收益=收入-成本关系得到六种策略组合企业和养老需求者的收益。由于需要双方各自利益最大化,则考虑企业和养老需求者双方的总利益,于是将六种策略组合的收益矩阵整理为企业-养老服务需求者双方总收益表。六种策略组合总收益下表3所示。 纯策略均衡分析法得到策略Ⅲ、Ⅴ的企业和养老需求者双方各自收益都最大化,再考虑总收益最大化。通过上表中得到策略Ⅲ、Ⅴ的总收益表达式为:策略Ⅲ:R1-C1-C2+W3;策略Ⅴ:W1-I2-C2。再根据企业收益和养老需求者的参数大小关系得策略Ⅲ的总收益大于策略Ⅴ,所以采用策略Ⅲ:企业进入养老产业和老人选择机构养老。 3 结论 通过“企业-老人”博弈模型,得双方收益最大化策略,即企业积极发展养老服务事业,需要养老服务的老年人则选择合适机构享受养老服务。本文整理几点措施:措施一:老年人口增加,市场规模增大,市场竞争必将更激烈。想在养老的新兴行业中取得领先地位,需尽早进入市场,把握商机。措施二:机构养老将会成为养老模式主流,但对企业的硬实力提出了更高要求。企业需要在資金充足的情况下完善硬件水平,合理采购硬件设备,利用空窗期减低运营成本。 参考文献 [1] 徐明江,赵云仙,尤剑鹏,王碧艳,黎赵.南宁市老年人社区居家养老意愿及影响因素研究[J].中国全科医学,2020 [2] 姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2011 [3] 杨敏慧.居家养老服务市场中的博弈分析[J].法制与社会,2019

