基于模糊自适应的倒立摆控制系统研究

高梦星 孙彦超 刘伯玉

摘  要： 针对二级倒立摆系统的非线性、自然不稳定特点，本文基于SIMULINK仿真环境下验证了模糊控制理论在二级倒立摆的控制中的有效性。通过对倒立摆系统的研究，建立了倒立摆系统的空间状态方程，从数学的角度对其进行精确建模。模糊控制器作为基于模糊理论发展起来的控制策略，凭借其智能性和自适应的特点，在一些复杂的系统中得到了应用。本文利用SIMULINK的模糊控制工具箱构建了两输入一输出的模糊控制器，设计了相应变量隶属度函数，构建了模糊规则。构建成功的模糊控制器应用于二級倒立摆控制的仿真中，通过观察小车和两级摆杆的位置、摆角等物理量，证明了在模糊控制下，二级倒立摆系统在较短的响应时间内便能够达到稳定状态，具备很好的动态性能以及较强的鲁棒性。

关键词： 二级倒立摆;模糊控制;SIMULINK

中图分类号： TP273+.4    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.10.059

本文著录格式：高梦星，孙彦超，刘伯玉. 基于模糊自适应的倒立摆控制系统研究[J]. 软件，2020，41（10）：229235

【Abstract】： In view of the nonlinear and natural instability characteristics of the double inverted pendulum system， this paper validates the effectiveness of the fuzzy control theory in the control of the double inverted pendulum based on the SIMULINK simulation environment. Through the study of the inverted pendulum system， the space state equation of the inverted pendulum system is established， and it is accurately modeled from the mathematical point of view. As a control strategy developed based on fuzzy theory， fuzzy controller has been applied in some complex systems by virtue of its intelligence and adaptive characteristics. In this paper， the fuzzy control toolbox of SIMULINK is used to construct a two-input and one-output fuzzy controller， the corresponding variable membership function is designed， and the fuzzy rules are constructed. The successfully constructed fuzzy controller is applied to the simulation of the two-stage inverted pendulum control. By observing the physical quantities such as the position and swing angle of the trolley and the two-stage pendulum rod， it is proved that under the fuzzy control， the two-stage inverted pendulum system has a shorter response. It can reach a stable state within a period of time， with good dynamic performance and strong robustness.

【Key words】： Double inverted pendulum; Fuzzy control; SIMULINK

0  引言

在典型的被控对象中可以对多种控制理论进行比较，并具有良好的延伸性，能够将其扩展到更高的维度。倒立摆系统就是这样的一个可以将理论应用于实际的理想实验平台。在对控制理论进行研究之际，极具典型性的一类实验设备便是倒立摆系统，其优势为无需太高造价，结构不复杂，同时可以十分方便的对其结构以及物理参数进行调整，其还具备不少变量，属于非线性且阶次较高的系统，但不够稳定。在研究以及验证控制理论方面具备不错的契合度，同时还能对数类存在差异的控制策略进行对比。

国内外现状：20世纪50年代，便有了研究倒立摆方面的内容，率先进行此方面研究的是来自于麻省理工大学的专家，同时对发射火箭之际其助推器进行工作的相关原理，将首台一级线性倒立摆研发出[1]。之后，倒立摆相关的概念被正式提出[2]。由于倒立摆并不是一种线性的存在，同时不够稳定，具备快速的特征，因此这一研究课题具备不小的难度，而这则使相关专家以及学者的关注度提升了不少[3]。到20世纪70年代，大家渐渐的在各类倒立摆内运用不同的控制策略，而PID以及LQR控制策略还有极点配置算法在各类控制策略中具备典型性[4-5]。一直到80年代末，在进行生产之际，LQR这一控制策略得到了十分宽广的应用，最终所获的效果也颇为不错。1985年时，尹征琦这位来自于西安交大的教授在对模糊控制器进行设计之后，成功控制了倒立摆，同时得到了成功运用[6]。“隶属云模型”的提出时间为1997年，其提出者为李德义团队，这一模型没有太多关于硬件方面的要求，因此所产生的控制效果不错[7]。“变论域自适应模糊控制理论”被提出的时间是1995年，其提出者为李洪兴教授，这一研究以稳定的方式对“四级倒立摆系统”进行了控制，紧接着使控制二级以及三级摆得以完成[8]。文献[9]设计了模糊PID控制器，对拉格朗日函数方式进行利用，将一个数学方面的二级倒立摆模型构建起来，通过现代控制理论研究了系统的稳定性、可控性和能观性，得到系统的控制条件，设计了模糊控制规则和推理过程。其所设计的控制方法要优于单独的模糊控制、PID控制。文献[10]设了一种基于直线二级倒立摆的双闭环模糊控制方法，该方法是将控制器的多变量输入分成两组，形成两个闭环，内环对倒立摆所具备的角度进行控制，外环则对倒立摆小车所处的具体位置进行控制。

就倒立摆而言，这一研究对象并不稳定，只要增加摆杆的数量，就会让其变得愈发难以控制[11]，与此同时，想要将一个具备不错精准度的数学模型构建起来也不容易，因此在进行此方面研究之际，所有学者都感到步履维艰由于现目前所应用到的智能控制中，只有模糊控制和神经网络控制不依靠于具体的数学模型。因此，有必要将模糊控制和神经网络算法控制引入到多级倒立摆系统中进行研究，本文就是基于自适应控制对其进行了较为深入的研究。

1  二级倒立摆系统建模

为完成以稳定的方式对倒立摆进行控制方面的研究，第一步必须把其数学模型构建起来，如此方可实施下一步应该实施的仿真程序。在构建模型之际，其方式可做两类划分：实验以及机理建模。前者便是将研究者已经准备好的输入信号添加到研究对象上面，对研究对象进行激励，同时对传感器加以利用，进行具体输出的相关检测，通过数学方式，将系统所具备的输入以及输出关系构建起来。所涵盖的内容有设计以及选择输入信号、精准的对输出信号进行检测，研究具体的数学算法。后者则首先需要掌控研究对象所具备的运动规律，同时基于此采取物理抑或是化学方面的知识还要U相关的数学方法将存在于系统内部的输入以及输出关系构建起来。

1.1  直线二级倒立摆的数学模型

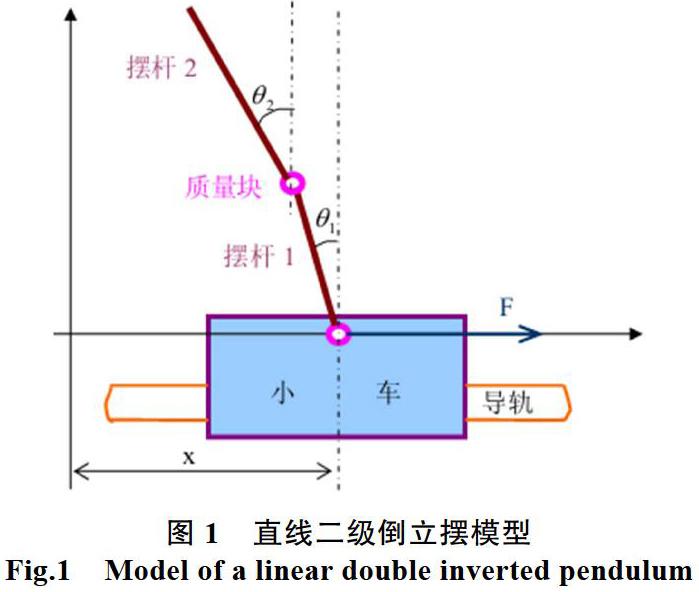
由于对牛顿力学加以利用实施建模之际，必须运用不少微分方程，因此构建二级倒立摆模型之际，建模会因为这些微风方程而出现复杂程度上升的情况，因此此篇文章通过对隶属于分析力学范畴的Lagrange方程加以利用實施建模[21]。图1所呈现的模型便是二级倒立摆。

首先，对该系统做如下假设：

（1）小车、一级摆杆和二级摆杆都是刚体。

（2）皮带轮与同步带之间无相对滑动，且同步带不会拉伸变长。

（3）小车与导轨之间的摩擦力与小车速度成正比。

（4）各级摆杆与转轴间的转动摩擦力矩与摆杆的角速度成正比。

本次控制系统采用的二级倒立摆各物理参数取值如表1所示。

1.2  倒立摆系统的定性分析

对二级倒立摆进行分析，使用MATLAB中的dg（）命令得系统开环特征为

因为系统有两个根在S平面的右半平面上，所以系统是不稳定的。

从定理1以及定理2两个存在于2.2.1中的式子可以看出，在对存在于MATLAB内的rank（）命令加以利用之后，便能够算出rank（S）=6和rank（V）=6。因此，系统可以进行观测以及控制。因此能够设计这一系统内的控制器，让系统变得更为稳定。

按照二级倒立摆状态方程（2-11），对存在于MATLAB内的命令[U，S，V]=svd（A）加以利用，通过奇异值分解的方式处理A矩阵，可将其奇异值阵S获取。

二级倒立摆的相对可控度：

δ=1/102.7083=0.0097。

模糊控制系统的原理图如图2所示。

2  基于MATLAB/SIMUNLINK的二级倒立摆控制仿真

在MATLAB/SIMULINK仿真平台中对基于模糊控制器的二级倒立摆进行建模仿真，建立的仿真模型如图3所示。

其中二级倒立摆的数学模型用状态空间方程进行模拟，其参数设置界面如图4所示。

通过设置状态空间方程的各参数便能够从数学的角度建立出二级倒立摆的模型。

控制器采用模糊控制器，在模型中对模糊控制器进行了封装，封装成一个子系统以提高仿真模型的集成度，模糊控制器的内部结构图如图5所示。

本次模糊控制器的结构采用了两输入一输出的系统，其编辑器的模型如图6所示。

在模糊控制系统的编辑器界面中可以设置和查看各输入量和输出量的隶属度函数，误差e、误差变化率ec和输出u的隶属函数见图7—图8所示。

在该编辑器中可以编辑和查看模糊控制器的模糊规则[30]，本文中的模糊控制器的模糊规则如图10所示。

本文设计的模糊控制中共有49条模糊规则。是根据输入论域和输出论域上的模糊语言变量划分而进行设计的：

把上述规则写成模糊规则表，如表2所示。

另外，在系统中为了清楚地观察二级倒立摆的控制性能，用示波器对一些物理量进行观测，本系统中观测的物理量有小车位移、小车速度、上摆杆角度、上摆杆角速度、下摆杆角度、下摆杆角速度等物理量。

运行仿真模型，在示波器中观察各物理量的变化情况。

小车位移波形曲线如图11所示。

小车速度波形如图12所示。

上摆杆的角度波形如图13所示。

上摆杆的角速度波形如图14所示。

下摆杆的角度波形如图15所示。

下摆杆的角速度波形如图16所示。

通过仿真试验，在示波器中观察各物理量，能够容易看出，小车的位置以及两级倒立摆的摆杆的角度都得到了有效控制，响应速度很快，在3s以内便达到了平衡。证明了模糊控制器在二级倒立摆系统中的控制优越性。

3  结论

二级倒立摆作为倒立摆系统研究的热点，近年作为典型的被控对象被广泛应用于控制理论的研究中。二级倒立摆系统的非线性、自然不稳定特点对于控制理论提出了挑战，多变量和强耦合性使其在建模中存在较大的困难。本文主要工作就是以二级倒立摆作为被控对象，在MATLAB/SIMULINK仿真环境下验证了模糊控制理论在二级倒立摆的控制中的有效性。通过对倒立摆系统的研究，建立了倒立摆系统的空间状态方程，从数学的角度对其进行精确建模。模糊控制器作为基于模糊理论发展起来的控制策略，凭借其智能性和自适应的特点，在一些复杂的系统中得到了应用。本文利用SIMULINK的模糊控制工具箱构建了两输入一输出的模糊控制器，设计了相应变量隶属度函数，构建了模糊规则。构建成功的模糊控制器应用于二级倒立摆控制的仿真中，通过观察小车和两级摆杆的位置、摆角等物理量，证明了在模糊控制下，二级倒立摆系统在较短的响应时间内便能够达到稳定状态，具备很好的动态性能以及较强的鲁棒性。

4  展望

本文在二级倒立摆的模糊控制研究方面取得了一定的成果，但由于个人水平和时间所限，仍然有很多工作需要后续深入研究。

（1）本文主要研究了二级倒立摆系统，目前已经有学者在对四级倒立摆进行研究，后续的工作可以围绕三级甚至更多级数的倒立摆系统进行研究;

（2）模糊控制具有自适应的特点，这是其优势，但是单纯的模糊控制有响应速度慢等问题，因此可以考虑模糊控制同PID控制等传统控制策略相结合的方式，以提高倒立摆系统控制的动态特性;

（3）目前控制理论发展迅速，更多的智能控制理论出现在控制器设计中，例如最优控制、神经网络控制等，后续可以尝试采用更智能的控制策略;

（4）本文的理论验证是在MATLAB/SIMULINK仿真环境下进行的，后续可以考虑在实际的二级倒立摆试验台中对控制策略进行实物验证。

参考文献

[1]邢景虎， 陆华才. 二级倒立摆两种控制方法的对比研究[J]. 佳木斯大学学报（自然科学版）， 2017， 35（2）： 263-266.

[2]侯涛， 董海鹰. 直线二级摆的双闭环串级模糊控制研究[J]. 兰州交通大学学报， 2008（1）： 99-102.

[3]郭波， 邹丽梅， 钱学毅. 基于模型仿真技术的PID参数整定优化[J]. 制造业自动化， 2015， 37（15）： 22-24.

[4]Knowlton E. Barber， John F. Adams， Leonard D. Sosinski. Control of Incontinent Urine by Using External Drainage[J]. AJN， American Journal of Nursing， 1949， 49（8）： 15-19.

[5]Yin， Jialin. Research on the Optimization PID Parameters based on Genetic Algorithm[J]. EN， 1974， 7（11）： 21-22.

[6]李志刚， 宣树人. 改进遗传算法优化设计模糊控制系统的研究[J]. 自动化仪表， 2016， 37（12）： 5-9.

[7]田力勇. 基于模糊神经网络的三级倒立摆稳定控制研究[D]. 燕山大学， 2011. 7（3）： 10-11.

[8]焦灵侠. 模糊控制在倒立摆系统中的应用研究[D]. 西安工业大学， 2010. 2（2）： 5-11.

[9]赵明明. 基于PID的二级倒立摆控制器的设计[D]. 曲阜师范大学， 2012. 3（2）： 10-14.

[10]侯涛， 董海鹰. 直线二级摆的双闭环串级模糊控制研究[J]. 兰州交通大学学报， 2008（1）： 99-102.

[11]Torsten Bertram， Ferdinand Svaricek. Zur Fuzzy-Regelung eines aufrechtstehenden Pendels/On Fuzzy-control of an inverted pendulum[J]. at-Automatisierungstechnik， 2014， 40（8）： 78-88.

[12]张新荣， 马杰， 张才斗， 等. 基于MATLAB倒立擺可视化建模仿真与控制[J]. 计算机工程与设计， 2018， 39（10）： 3214-3219.

[13]齐心舒. 智能控制算法设计及倒立摆实现[D]. 内蒙古大学， 2018.

[14]马杰. 基于Matlab/Simulink的环形倒立摆建模与控制方法实验研究[D]. 长安大学， 2018.