基于混沌和四进制系统的图像加密算法

田妙妙 刘晔 龚黎华

摘  要： 信息时代对图像传输安全性要求较高，针对此问题提出一种将5D超混沌与四进制系统相结合的数字图像加密算法。5D超混沌的初值通过汉明距离与明文图像紧密相连，因此该图像加密方案能够有效抵抗选择明文攻击和已知明文攻击。在置乱阶段，明文图像被分解为4幅四进制图像。在密钥流的控制下，完成四进制图像像素位置的全局置乱。在扩散阶段构造一种基于四进制的循环操作来扩散图像的像素值。将扩散后的4个四进制矩阵转换为相应的十进制矩阵，并对该矩阵与密钥流进行加法运算即可得到加密图像。仿真结果和性能分析表明，该图像加密方案性能优越，安全性高。

关键词： 图像加密; 5D超混沌; 四进制系统; 图像分解; 矩阵转换; 仿真分析

中图分类号： TN911.73?34; TN915.08                  文献标识码： A               文章编号： 1004?373X（2020）23?0049?05

Abstract： The high security of image transmission is required in the information age. Therefore， a digital image encryption algorithm based on 5D hyper chaos and quaternary system is proposed. The initial values of 5D hyper chaos are closely connected with the plaintext image by Hamming distance， so the image encryption scheme can effectively resist the chosen?plaintext attack and the known plaintext attack. In the scrambling phase， the plaintext image is decomposed into four quaternary images. The global scrambling of the pixel position of the quaternary images is completed under the control of the key flow. In the diffusion phase， a kind of cycle operation based on quaternary system is built to diffuse the pixel values of the image. The 4 diffused quaternary matrices are converted into corresponding decimal matrices， and an additive operation is performed for the decimal matrices and key stream to achieve the encrypted image. Simulation results and performance analyses demonstrate the superior performance and high security of the image encryption scheme.

Keywords： image encryption; 5D hyper chaos; quaternary system; image decomposition; matrix transformation; simulation analysis

0  引  言

图像作为信息传递的一种载体，能够生动直观地传递信息。今天，由于互联网的快速发展，数字图像已经广泛应用于社会、政治、经济、军事等领域。同时，图像安全越来越受到人们的重视，图像加密是解决图像安全问题的重要途径。

混沌是洛伦兹于1963年发现的，在非线性科学领域中经常被提及。混沌由于其固有的遍历性、伪随机性、不可预测性、对初值和控制参数极度敏感等特性，在图像加密中得到了广泛的应用[1?2]。1998年，Fridrich提出了第一个基于二维和三维混沌映射的高效图像加密算法。此后，人们构建了一系列基于不同混沌系统的图像加密方案，包括低维混沌系统[3]、超混沌系统[4]和时空混沌系统[5]。低维混沌系统能够快速生成混沌序列，但由于密钥空间小、安全性差，很少单独用于加密算法的设计。将低维混沌与具有更好混沌特性的高维混沌相结合，可以克服这一缺陷[6]。文献[7]在2015年提出了一种基于高维混沌映射的图像加密方案，该加密方案抵抗选择明文攻击的能力较弱[8?9]。图像加密方案之所以无法有效抵抗已知明文攻击和选择明文攻击是因为用于位置置亂和像素值替换的密钥流的产生，与明文图像没有关系。为了克服文献[7]中出现的问题，文献[10]提出基于混沌和DNA序列的位级图像加密方案。在该方案中，将明文图像的像素值总和进行预处理之后用于改变混沌系统的初始值。实验结果表明该方案虽然可以有效抵抗已知明文攻击和选择明文攻击，但是该加密方案对裁剪攻击的抵抗力较弱。文献[11]提出了一种基于二维超混沌系统的图像加密方案[11]。实验结果表明，该图像加密算法也解决了文献[7]中存在的问题，但是该加密方案抵抗裁剪攻击和噪声攻击的能力较弱。

为了克服上述缺点，本文提出了一种基于5D超混沌和四进制循环操作的图像加密算法。与一般的混沌系统相比，5D超混沌系统拥有更多的参数，可以更好地抵抗穷举攻击。此外，为了使密钥流的产生与明文图像紧密相关。将四进制图像两两之间的汉明距离进行处理，并将其代入混沌系统作为混沌系统迭代运算的初值。置乱时，在密钥流的控制下，对4幅四进制图像的像素位置进行交叉互换完成全局置乱，这种置乱方式不仅有置乱效果而且还有扩散效果。循环操作用于在扩散阶段改变4幅四进制图像的像素值。实验结果表明，该图像加密方案不仅可以有效抵抗已知明文攻击和选择明文攻击，而且具有较好的抵抗裁剪攻击和噪声攻击的能力。

1  基本理论

1.1  5D超混沌

与一般混沌系统相比，5D超混沌系统[12]具有更复杂的动态特性和更高的随机性，更适合于图像加密。

1.3  汉明距离

两个长度相等的字符串之间的汉明距离是两个字符串之间不同字符的个数，即将一个字符串转变为另一个字符串时所需要更换的字符数。假设一个字符串是′132424′，另一个字符串是′342123′。那么，这两个字符串之间的汉明距离是4，因为要使两个字符串相同，需要替换4个字符。

在本文中，5D超混沌系统的初值可以通过4幅四进制图像之间的汉明距离来改变，从而使混沌序列与明文信息密切相关。

2  加密算法和解密算法

2.1  密钥流的产生

图像加密所需的混沌序列可以通过如下方式生成。

步骤1：通过1.2节所述方式将明文图像分解为4幅四进制图像[P1]，[P2]，[P3]，[P4]。

步骤8：将一维矢量[C2]转换为二维图像[C2M，N]，完成加密过程。

用密钥流解密密文图像是加密过程的逆过程。

3  仿真结果和分析

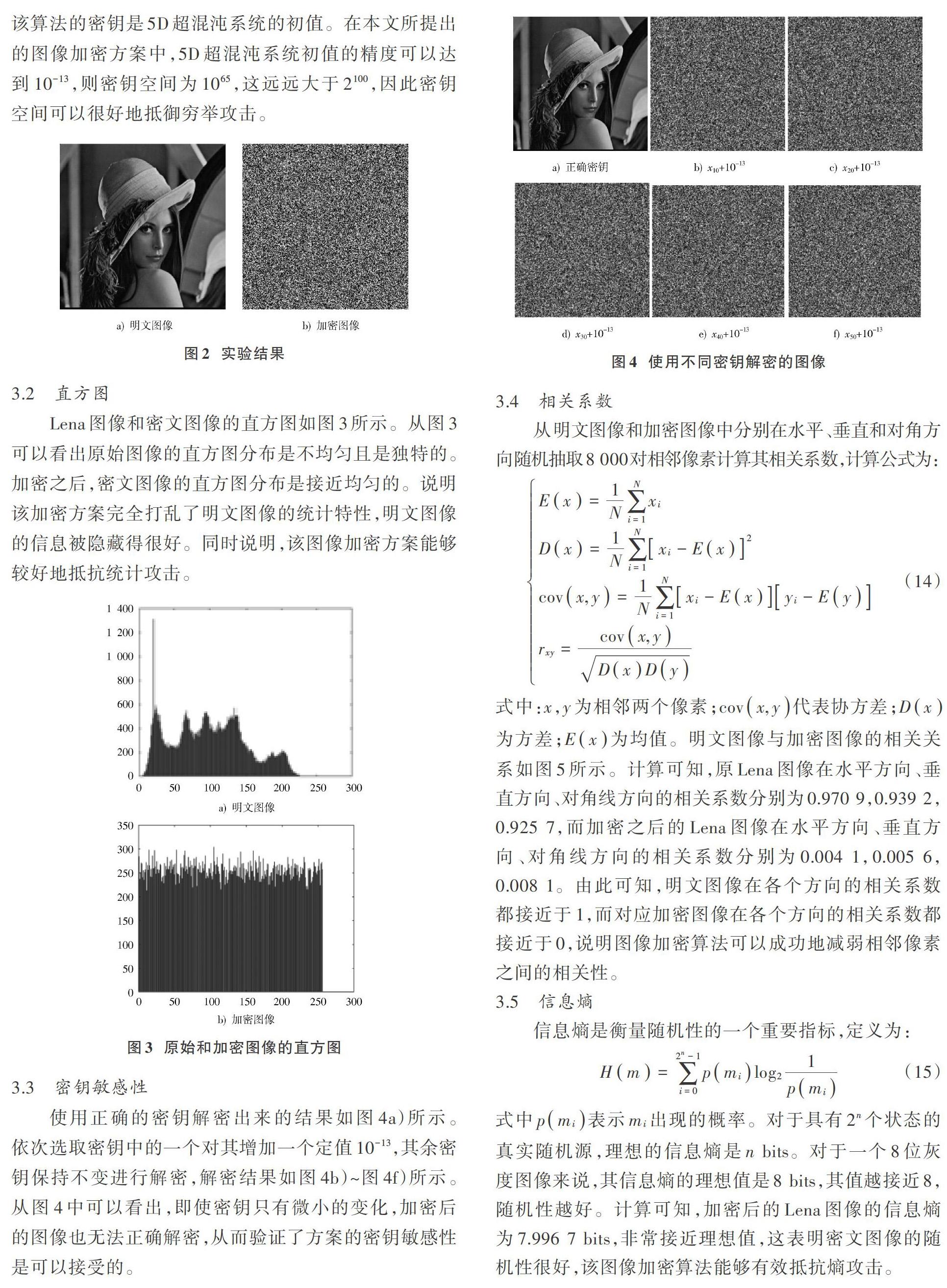
本节在Windows 10，64位操作系统的PC机上，用Matlab R2016a对Lena图像进行了测试。5D超混沌的初值分别为[0.123 0]，[0.637 7]，[0.747 6]，[0.573 8]，[0.635 0]。如图2所示的实验结果表明用该加密方案对明文图像进行加密之后，从加密图像中得不到任何关于明文图像的信息，而且可以通过解密流程还原出明文图像，从而说明该图像加密方案是可行的。

3.1  密钥空间

理论上，如果加密系统的密钥空间大于[2100]，则认为在当前计算速度下，加密系统可以有效抵御穷举攻击。该算法的密钥是5D超混沌系统的初值。在本文所提出的图像加密方案中，5D超混沌系统初值的精度可以达到[10-13]，则密钥空间为[1065]，这远远大于[2100]，因此密钥空间可以很好地抵御穷举攻击。

3.2  直方图

Lena图像和密文图像的直方图如图3所示。从图3可以看出原始图像的直方图分布是不均匀且是独特的。加密之后，密文图像的直方图分布是接近均匀的。说明该加密方案完全打乱了明文图像的统计特性，明文图像的信息被隐藏得很好。同时说明，该图像加密方案能够较好地抵抗统计攻击。

3.3  密钥敏感性

使用正確的密钥解密出来的结果如图4a）所示。依次选取密钥中的一个对其增加一个定值[10-13]，其余密钥保持不变进行解密，解密结果如图4b）～图4f）所示。从图4中可以看出，即使密钥只有微小的变化，加密后的图像也无法正确解密，从而验证了方案的密钥敏感性是可以接受的。

3.4  相关系数

从明文图像和加密图像中分别在水平、垂直和对角方向随机抽取8 000对相邻像素计算其相关系数，计算公式为：

[Ex=1Ni=1NxiDx=1Ni=1Nxi-Ex2covx，y=1Ni=1Nxi-Exyi-Eyrxy=covx，yDxDy] （14）

式中：[x]，[y]为相邻两个像素;[covx，y]代表协方差;[Dx]为方差;[Ex]为均值。明文图像与加密图像的相关关系如图5所示。计算可知，原Lena图像在水平方向、垂直方向、对角线方向的相关系数分别为0.970 9，0.939 2，0.925 7，而加密之后的Lena图像在水平方向、垂直方向、对角线方向的相关系数分别为0.004 1，0.005 6，0.008 1。由此可知，明文图像在各个方向的相关系数都接近于1，而对应加密图像在各个方向的相关系数都接近于0，说明图像加密算法可以成功地减弱相邻像素之间的相关性。

3.5  信息熵

信息熵是衡量随机性的一个重要指标，定义为：

[Hm=i=02n-1pmilog21pmi] （15）

式中[pmi]表示[mi]出现的概率。对于具有[2n]个状态的真实随机源，理想的信息熵是[n] bits。对于一个8位灰度图像来说，其信息熵的理想值是8 bits，其值越接近8，随机性越好。计算可知，加密后的Lena图像的信息熵为7.996 7 bits，非常接近理想值，这表明密文图像的随机性很好，该图像加密算法能够有效抵抗熵攻击。

3.6  明文敏感性

[NPCR]（像素数变化率）和[UACI]（归一化平均变化强度）可用于揭示图像之间的差异。它们的定义如下：

式中：[M]和[N]分别为图像矩阵的行数和列数;[T1x，y]是与明文图像对应的加密图像;[T2x，y]为明文图像改变一个像素值后对应的加密图像。对于一幅8位灰度图像，[NPCR]和[UACI]的期望值分别为99.60%和33.46%。由本文方案计算出来的[NPCR]和[UACI]分别为99.604 6%和33.438 7%，与期望值非常接近，这表明即使两幅明文图像只有一个像素值是不同的，其加密之后得到的密文图像差别也很大，因此该图像加密算法能够有效抵抗差分攻击。

4  结  语

本文提出了一种基于5D超混沌和四进制循环操作的图像加密算法。5D超混沌参数较多，对初始值极为敏感，因此该图像加密算法能够更好地抵御穷举攻击，为算法的安全性提供一定的保障。将明文图像分解为4幅四进制图像后在密钥流的控制下完成置乱，基于四进制的循环操作用于扩散像素值。加法操作进一步扩散了像素值，使得相邻像素之间的相关性接近于0。实验结果表明，该算法能够有效地抵抗穷举攻击、统计攻击、差分攻击等多种攻击，是一种符合安全要求的图像加密算法。

参考文献

[1] WU Xiangjun， WANG Kunshu， WANG Xingyuan， et al. Lossless chaotic color image cryptosystem based on DNA encryption and entropy [J]. Nonlinear dynamics， 2017， 90（2）： 855?875.

[2] LI Yueping， WANG Chunhua， CHEN Hua， et al. A hyper?chaos?based image encryption algorithm using pixel?level permutation and bit?level permutation [J]. Optics and lasers in engineering， 2017， 90： 238?246.

[3] ?AVU?O?LU ?， KA?AR S， PEHLIVAN I， et al. Secure image encryption algorithm design using a novel chaos based S?box [J]. Chaos， solitons and fractals， 2017， 95： 92?101.

[4] NIYAT A Y， MOATTAR M H， TORSHIZ M N. Color image encryption based on hybrid hyper?chaotic system and cellular automata [J]. Optics and lasers in engineering， 2017， 90： 225?237.

[5] GUO Shaofeng， LIU Ye， GONG Lihua， et al. Bit?level image cryptosystem combining 2D hyper?chaos with a modified non?adjacent spatiotemporal chaos [J]. Multimedia tools and applications， 2018， 77（16）： 21109?21130.

[6] PAK C， HUANG Lilian. A new color image encryption using combination of the 1D chaotic map [J]. Signal processing， 2017， 138： 129?137.

[7] TONG X， ZHANG M， WANG Z. A new image encryption algorithm based on the high?dimensional chaotic map [J]. The ima?ging science journal， 2015， 63（5）： 263?272.

[8] AKHAVAN A， SAMSUDIN A， AKHSHANI A. Cryptanalysis of an image encryption algorithm based on DNA encoding [J]. Optics and laser technology， 2017， 95： 94?99.

[9] LI Zeng， LIU Renren. Cryptanalyzing a novel couple images encryption algorithm based on DNA subsequence operation and chaotic system [J]. Optik， 2015， 126（24）： 5022?5025.

[10] LIU Ye， LIN Tao， WANG Jun， et al. Bit image encryption algorithm based on hyper chaos and DNA sequence [J]. Journal of computers， 2018， 29（3）： 43?55.

[11] YUAN Hongmei， LIU Ye， GONG Lihua， et al. A new image cryptosystem based on 2D hyper?chaotic system [J]. Multimedia tools and applications， 2017， 76（6）： 8087?8108.

[12] FAN Bing， TANG Liangrui. A new five?dimensional hyperchaotic system and its application in DS?CDMA [C]// 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery. Sichuan， China： IEEE， 2012： 2069?2073.