生态系统服务价值时空变化及分布均匀度变化分析
张玉娟,曲建光,王 雷
(黑龙江工程学院测绘工程学院,黑龙江 哈尔滨 150050)
0 引言
生态系统服务是生态系统形成和变化过程中提供给人类生存与发展所需要的各种效用[1-2],是链接生态系统与社会经济系统的桥梁[3]. 生态系统服务能力是综合评价生态环境优劣和生态经济价值的重要指标. 对生态系统服务价值(ecosystem services value,ESV)进行定量评估已成为生态学、 地理学、 环境经济学的热点和前沿问题[4]. ESV分布均匀度是指不同等级的ESV在数量和空间上分布的均匀程度. 通过分析不同等级的ESV数量与空间的分布均匀度可以为研究区域景观格局调整提供新的参考,以实现小代价换取区域ESV增值的目的.
1997年,Costanza在《Nature》中第一次提出了ESV估算原理和方法[5]. 近30年各国学者研究了多种ESV估算方法,其中国内参考量最高的是谢高地团队[6]依据Costanza等研究的部分成果,对中国近200位生态学者进行问卷调查,制定出中国区域ESV当量因子表. 谢高地团队于2006年又对中国500位生态学者进行问卷调查,得出新的生态系统服务评估体系,并于2015年进行修订[7]. 很多国内学者以谢高地团队的研究为基础,根据各自研究区域情况调整生态服务当量因子表,估算研究区域ESV,为区域生态环境建设提供依据. 其中较多研究集中在景观格局变化对生态系统服务价值的影响上[8-9]. 也有部分研究集中在生态系统服务价值权衡协同关系上[10-11]. 近年来,在生态系统服务的研究上注重景观格局变化对ESV的影响和ESV权衡协同关系,对ESV空间分布特征研究较少,对ESV的分布均匀度更是未见研究.
近20年,松花江流域哈尔滨段草地减少,盐碱地增加,自然植被用地转化频繁,土地利用结构趋于不稳定状态[12-13],不断变化的土地利用方式必然导致ESV时空分布的变化. 目前对该区域在景观格局、 粮食安全和水环境评价方面有较多的研究[14-17]. 对该区域综合ESV定量评估研究文献只有1篇:龚文峰等[18]针对研究区域2006年和2005年ESV总量进行计算,但学者并未实现区域小单元划分,没有进行ESV空间分布变化研究,且所研究的年限较为久远.
鉴于此,本文以松花江流域哈尔滨段为研究区域,以谢高地ESV模型[7]为基础,修正本研究区域的ESV模型,对区域进行网格划分,通过地统计学及空间相关分析方法对研究区域ESV时空变化特征及空间相关性进行研究. 引入信息熵均匀度理论和独占圆被含均匀度理论对研究区域不同等级的ESV在数量分布和空间分布的均匀度进行计算与变化分析. 研究成果有助于完善松花江流域哈尔滨段的生态格局,并为其它研究区域ESV分布均匀度的研究提供范例.
1 数据来源及研究方法
本文数据来源及处理过程、 获得的松花江流域哈尔滨段1995年、 2005年和2015年景观类型分布图,参见参考文献[16]. 考虑数据可获取性,在计算ESV时,本文将9个辖区合并为主城区.
1.1 ESV计算
1.1.1ESV计算公式
根据谢高地团队给出的ESV计算方法[7],按下式计算区域ESV总价值.

(1)
式中:VEStotal为ESV总量,VCij为第i类景观对应第j类型服务的单位面积ESV(元·hm-2);Si为研究区第i类景观类型面积(hm2);n为景观类型个数.
1.1.2单位面积ESV当量表修订
谢高地团队在2015年研究所得的单位面积ESV当量表[7]是基于二级生态系统分类的,本研究所确定的生态系统分类为一级分类,且与谢高地团队的一级分类结果存在差异,需要对单位面积ESV当量表进行修订. 根据本研究区域景观特征,将其中的草地、 未利用地与谢高地团队二级分类结果中的草甸、 裸地相对应,本研究区域冬季11月至次年2月为霜期,3—10月为无霜期,将谢高地团队当量表中二级分类的水系与冰川积雪按3∶1加权计算本研究区域水体当量. 通过查阅哈尔滨市1996年、 2006年和2016年统计年鉴,2015年林业志等参考资料,统计研究区域、 县域及主城区林地主要二级类型面积比例,按二级分类面积比例加权计算各区域林地的服务价值当量. 研究区同一区域不同年份耕地中水田与旱田面积比例变化较大,通过查阅哈尔滨市统计年鉴,获得不同年份区域、 县域及主城区耕地主要二级类型面积比例,按二级分类面积比例加权计算各区域耕地服务价值当量. 依据哈尔滨市2013年城市绿化普查数据及Google Earth地图数据,计算建设用地中含主要生态景观面积比例和非生态景观面积比例,按各类景观对应面积比例加权计算建设用地服务价值当量.
1.1.3ESV当量因子修正
ESV的变化具有时间和空间效应,谢高地团队将2010年全国单位面积农田生态系统粮食生产的净利润当作1个标准当量因子,确定中国2010年1个生态系统价值当量的经济价值为3 406.50元·hm-2. 根据《2010年哈尔滨市统计年鉴》,哈尔滨市耕地地均粮食产量为6.059 1 t·hm-2,同期全国地均粮食产量为5.152 4 t·hm-2,据此对本研究区域ESV当量因子进行修正,修正系数为2010年哈尔滨市耕地地均粮食产量与全国地均粮食产量比值1.176,得到区域内1个生态系统价值当量的经济价值为4 006.04元·hm-2,为了剔出通货膨胀引起的不同年份ESV差异,本研究所有年份ESV的计算均参照2010年当量因子计算结果.
1.2 基于半方差函数的空间变异结构拟合
空间变异结构可通过半方差函数的理论模型模拟,计算公式为[19]:

(2)
式中:γ(h)为变异函数值;Z(xi)和Z(xi+h)是Z(x)在空间单元xi和xi+h上的ESV(i=1, 2, 3, …,N(h));N(h)是分割距离h的样本量.
最优变异函数拟合模型的选择主要考虑决定系数R2取得最大值,残差值RSS取得较小值,并结合结构方差与基台值的比值Rc(该值反映了空间相关性的强弱,将它定义为空间相关系数,即该系数越大空间相关性越强,说明样本间的变异更多是由结构性引起的)以及有效变程A(变程值表示某一特征在空间上自相关的空间幅度,在大于变程的空间尺度上该变量没有自相关性).
1.3 ESV均匀度理论
1) 基于信息熵理论的均匀度. 信息熵最早由克劳德﹒香农提出,用于判断不同通信信号出现概率的均匀性,当不同信号出现概率呈现比较均匀分布时所能呈现的信息量较大,当不同的信号出现概率呈现不均匀分布时所能呈现的信息量较小[20]. 其计算公式为:

(3)
式中:H为信息熵;n为不同信号个数;pi为信号i出现概率.
在景观生态学中基于信息熵理论的均匀度用来描述景观里不同生态系统的分配均匀程度,其计算公式为:
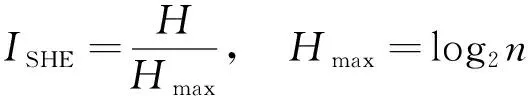
(4)
式中:ISHE为基于信息熵理论的均匀度指数;H为信息熵;Hmax为理论最大均匀信息.
本文引入信息熵理论,将计算获得的ESV按照大小进行相等间隔法等级划分,将不同等级的ESV看成不同信号,统计网格不同等级ESV出现的概率,通过式(3)~(4)计算研究区域三期ESV基于信息熵理论的均匀度,该均匀度可衡量研究区域不同等级ESV在数量上分布的均匀程度,不能衡量空间分布的均匀程度.
2) 独占圆与被含均匀度理论. 独占圆与被含均匀度理论最早由罗传文教授[21]提出,用于判断林分中植物格局的均匀程度,定义为:二维空间中具有相同属性的一组离散点Pi(i=1, 2, …,n),假设A∈Pi(i=1, 2, …,n),将距离点A的最近邻体点记为B,B∈Pi(i=1, 2, …,n),AB两点间距离称为点A的紧邻距离,记为D(A); 以A为圆心,以D(A)/2为半径的圆称为点A的独占圆,独占圆的任意外切正方形称为点A的独占体,则点A独占体面积记为S(A).
被含均匀度U被定义为离散点Pi(i=1, 2, …,n)独占体总面积与研究区域面积之比,计算公式为:

(5)
通过式(5)计算研究区域三期不同等级的ESV被含均匀度,该均匀度可衡量不同等级的ESV空间分布的均匀程度.
2 实验结果与分析
2.1 ESV计算
2.1.1ESV当量表
根据节1.1中单位面积ESV当量表修订方法,分别对主城区和6个县进行不同年份单位面积ESV当量表计算. 其中林地、 草地、 建设用地、 水域和未利用地对各种生态服务类型的单位面积ESV当量表见表1,耕地不同区县不同年份对各种生态服务类型的单位面积ESV当量表见表2.

表1 单位面积ESV当量表Tab.1 Equivalent scale of ESV per unit area
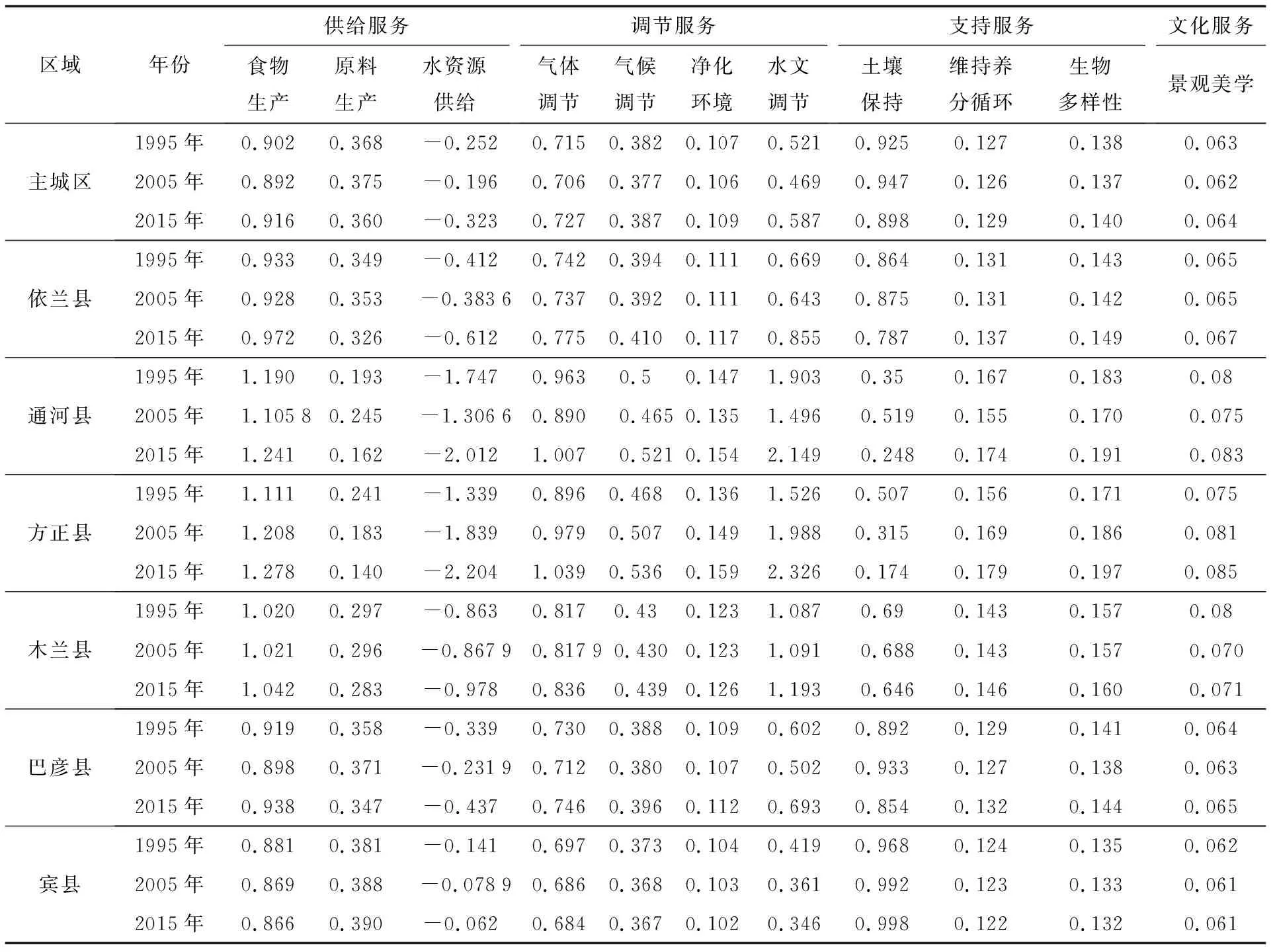
表2 耕地单位面积ESV当量表Tab.2 Equivalent scale of ESV per unit area of cultivated land
2.1.2网格划分及ESV计算
按照5 km×5 km尺度将研究区域划分成1 499个正方形单元,分别对三期按景观类型融合后的景观类型分布矢量、 网格矢量和区县边界矢量进行相交运算,获取每个斑块所属的网格、 景观类型和区县属性,根据表1~2和式(1)计算斑块ESV,再按所属网格进行合并,计算出三期网格ESV,结果见图1.

图1 5 km尺度ESV网格分布图Fig.1 Distribution of ESV at 5 km scale
2.2 基于半方差函数的空间变异结构拟合分析
在地统计学软件GS+的支持下,构造三期ESV变异函数模型,完成数据变异函数理论模型的拟合(见表3). 1995年、 2005年和2015年ESV分别为线性、 球状和指数模型拟合效果最好,决定系数R2分别为0.990、 0.993和0.826,残差值RSS均为最小值,结构方差与基台值的比值Rc均大于0.5,且呈现递增的变化,说明在5 km×5 km单元网格划分下,1995—2015年,结构性因素对ESV影响程度加深[22]. 1995年、 2005年和2015年ESV空间分异的变程分别为182.624、 229.100和53.100 km,表明5 km×5 km单元网格划分下研究区ESV具有高度的空间相关性.

表3 5 km尺度ESV变异函数拟合模型参数Tab.3 Parameters of ESV variation function fitting model at 5km scale
2.3 ESV时空变化分析
按照等间距法对ESV划分为最低值ESV、 低值ESV、 较低ESV、 中等ESV、 较高ESV、 高值ESV、 最高值ESV. 运用普通克里格插值法对划分ESV等级后的5 km尺度离散点进行插值生成三期ESV连续空间分布图(见图2).
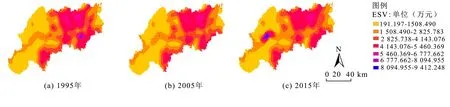
图2 ESV连续空间分布图Fig.2 Continuous spatial distribution of ESV
各级别ESV空间分布存在明显的异质性,最低值、 低值ESV主要分布在以耕地和建设用地为主的主城区、 巴彦县、 宾县和依兰县; 高值、 最高值ESV在2005年均没有分布,1995年分布在通河县与方正县交界以水域景观为主的网格分布区域,2015年分布在松花江位于主城区西部水域较宽区域; 较高值ESV主要分布在水域景观与其他景观交界处或林地景观中心区域,中等ESV主要分布在林地耕地交界处靠近林地一侧,较低ESV主要分布在林地耕地交界处靠近耕地一侧或狭窄水域景观与耕地景观交界处. 不同年份各级别ESV分布区域差异不大,不同级别ESV分布面积受景观类型转换影响,最高值、 高值ESV分布较大因素是受不同年份降雨量影响,2005年研究区域降水量小,以水域为主的景观网格没有形成聚集分布,导致高值、 最高值ESV均没有分布.
2.4 ESV分布均匀度变化
在进行ESV分布均匀度计算前,根据信息熵理论和独占圆与被含均匀度理论,按照相等间隔法对ESV进行5个不同等级的划分,即低值ESV、 较低ESV、 中等ESV、 较高ESV、 高值ESV.
2.4.1基于信息熵理论的均匀度变化与分析
分别对三期各等级ESV网格数量进行统计,计算不同等级ESV在数量上分布的均匀度,结果见表4,1995年、 2005年和2015年不同等级ESV数量分布均匀度分别为0.390 0、 0.366 3和0.389 6. ESV数量分布均匀度均比较低,源于研究区域内各级别ESV网格分布数量极不均衡,近50%的网格ESV都处于低值区域,近30%的网格ESV处于较低值区域,中等、 较高和高值ESV总网格数不足20%.

表4 三期各等级ESV网格数及均匀度Tab.4 Number of ESV grids at different levels and uniformity
由表1、 2可知,不同的景观类型单位面积产生的ESV差异较大,水域景观在单位面积上产生的服务价值最大,分别是林地、 耕地、 草地、 建设用地、 未利用地景观单位面积产生的服务价值的3.850 6倍、 22.066 6倍、 7.625 8倍、 41.704 8倍和435.815 0倍. 因此,当网格内水域面积比例较大时所能产生的ESV也非常大,研究区域内水域面积比例大的网格个数非常少,导致较高和高值ESV网格个数也非常少; 未利用地单位面积产生的服务价值非常小,但未利用地斑块面积也非常小,一般在网格内部所占面积非常小,对网格ESV影响不足以表现为使ESV出现极小值的情况; 耕地和林地为在研究区域优势景观,尤其是耕地景观作为基质占有最大比例的面积,当网格内主要为耕地景观时呈现低值ESV,网格内主要为林地景观时呈现较低ESV,因此低值ESV和较低ESV网格比例非常大. 三期不同等级ESV在数量分布均匀度总体上呈现先减小后增加的变化,主要由于相对于1995年和2015年,2005年研究区域内作为廊道的水域景观宽度较窄,没有网格范围内水域景观面积比例大到能使网格ESV值达到较高ESV和高值ESV的级别,在1995年和2015年零星分布的较高ESV和高值ESV网格在2005年都呈现为低值ESV和较低ESV,因此2005年各等级ESV分布较1995年和2015年更不均匀.
2.4.2独占圆与被含均匀度理论变化与分析
根据独占圆定义,以网格中心点坐标为独占圆圆心,将三期网格ESV等级值赋给中心点,在ArcGIS10.3中编写代码绘制每期不同等级ESV的独占圆(见图3),计算独占体面积及被含均匀度,结果见表5.

图3 不同等级ESV独占圆Fig.3 ESV exclusive circles of different levels
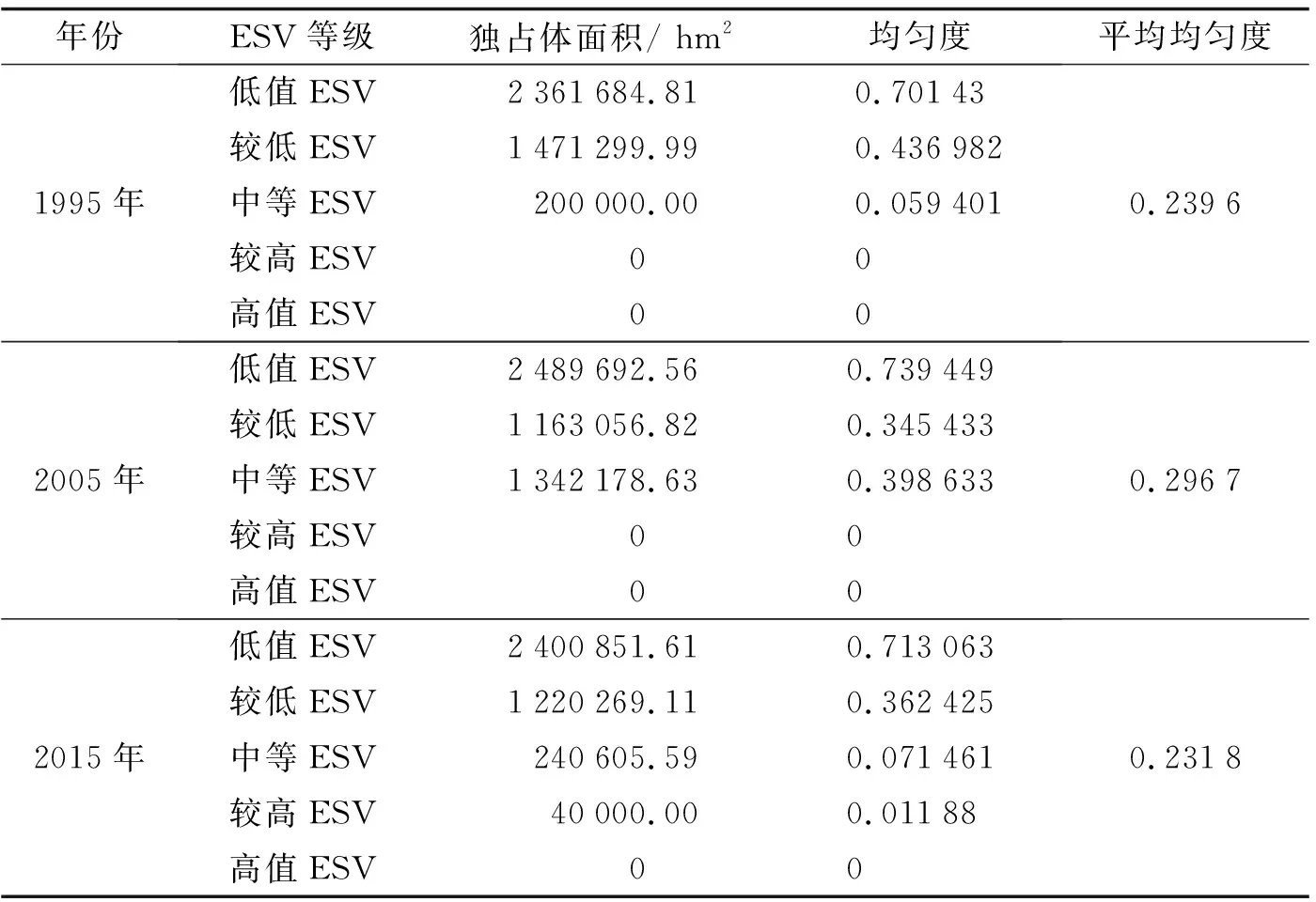
表5 ESV空间分布均匀度Tab.5 Spatial distribution uniformity of ESV
从表5可以看出,各等级ESV空间分布不均匀. 低值ESV空间分布均匀度均大于0.7,在研究区域内空间分布均匀,其余各等级ESV空间分布均匀性均小于0.5,都处于不均匀分布状态,尤其是较高、 高值ESV及1995年和2015年的中等ESV空间分布均匀性极低,源于这些等级ESV网格个数非常少,且较集中分布于局部范围内. 三期ESV平均空间分布均匀度均小于0.3,表现为不均匀空间分布,呈现增加后减小的变化,主要源于2005年中等ESV虽然在数量上分布非常少,但中等ESV网格较离散分布于研究区域内,因此2005年中等ESV空间分布均匀度较1995年和2005年高,致使2005年研究区域ESV空间分布均匀度高于1995年和2005年.
3 结语
研究区域ESV存在很强的空间相关性,各级别ESV空间分布存在明显的异质性,低值ESV主要分布在主城区、 巴彦县、 宾县和依兰县,高值ESV主要分布在以水域景观为主的网格分布区域,较高值ESV主要分布在水域景观与其他景观交界处或林地景观中心区域,中等ESV主要分布在林地耕地交界处靠近林地一侧,较低ESV主要分布在林地耕地交界处靠近耕地一侧或狭窄水域景观与耕地景观交界处,不同年份各级别ESV分布差异不大.
不同等级ESV在数量分布均匀度上呈现先减小后增加的变化,均匀度都比较低. 各等级ESV空间分布不均匀,低值ESV空间分布均匀度均大于0.7,在研究区域内空间分布均匀,其余各等级ESV空间分布均匀性均小于0.5,都处于不均匀分布状态,三期ESV平均空间分布均匀度呈现增加后减小的变化,分别为0.239 6、 0.296 7和0.231 8,均小于0.3,表现为不均匀空间分布.

