基于STM32 的AES 算法优化设计

赵亚亚 孙顺远，2

（1.江南大学物联网工程学院 无锡 214122）（2.江南大学轻工过程先进控制教育部重点实验室 无锡 214122）

1 引言

随着计算机和互联网技术的飞速发展，人类已经进入了大数据时代，数据已经成为人类活动中重要的生产因素。然而，随着近几年发生的数据泄露事件，引发了人们对信息安全问题的关注［1］。而数据加密技术可以对敏感信息进行加密，实现信息隐藏，为敏感信息提供了从发送方到接收方之间最安全的传输方案，保证了这些敏感信息对第三方的不可读性。

当前应用最为广泛的加密算法是高级加密标准AES 算法，它是一种对称加密算法，与非对称加密相比，其加密和解密速度优势显著。但随着物联网的发展，资源受限的设备已经无处不在，对算法的执行效率和存储空间提出了更高的要求。

原始的AES 算法［2］使用查表法，运行前先将S盒和逆S盒存储为两张256字节大小的表格（数组）中，再通过编程语言实现加解密过程。虽然该方法占用内存小，但实现过程复杂，效率低。斯托林斯［3］提出了通过牺牲内存空间提高执行效率的方法，将实现过程提前计算为8 张1024 字节的表格，然后通过查表和异或运算实现加解密过程，虽然提高了执行速度，但是在资源受限的情况下，此方法并不实用。赵跃华等［4］在此基础上，通过数学变换，将加解密过程中的迭代变换进行合并，找到了通过6张256字节的表实现AES的方法。而谢秀颖等［5］进一步优化为5 张256 字节的表，并运用查表法将算法应用到了物联网智能家居中，提升了效率，并减少了对存储空间的占用。魏国珩等［6］从硬件实现的角度，提出了使用电路复用技术将加解密过程进行合并优化的思路，并具有良好的表现。

不过由于AES 算法原理的公开化和普及化时间较长，也使得其安全性受到考验。张丽红等［7］针对加密过程中多次用到的S盒字节代换进行优化重构，解决了S盒迭代输出周期过短的问题，提高了S盒的安全性。本文将在文献［7］的基础上，对上述文献的软硬件实现方法进行分析，并综合考虑算法的安全性和执行效率两方面，对AES 进行优化改进，设计轻量高效的软件实现方法，并进行实验验证。

2 AES算法基础

美国国家标准与技术研究所（National institute of standards and technology，NIST）于1997 年发起了征集AES 的活动，经过三年多的讨论，最终在2001年确立将对称分组密码Rijndae 标准化为AES［8］。其数据分组长度和密钥长度并不是唯一的，而是可以指定为128位、192位、256位，但是相对应地需要10轮、12轮、14轮迭代加密操作。由于本文考虑的是在有资源限制的环境中运行，所以选择的是占用资源较低的128位AES算法（简记为AES-128）。

整个算法主要由密钥扩展、加密和解密三部分组成［8～10］。其整体实现如图1所示。

2.1 密钥扩展算法

对于AES-128，其密钥长度为128bit，也就是16 个字节。将密钥K 的每个字节填入到4*4 的矩阵中，经过10 轮的扩展，将4 列初始密钥扩展为44列的密钥W[i]，i ∈[0，43]。密钥扩展算法流程［11］如图2所示。

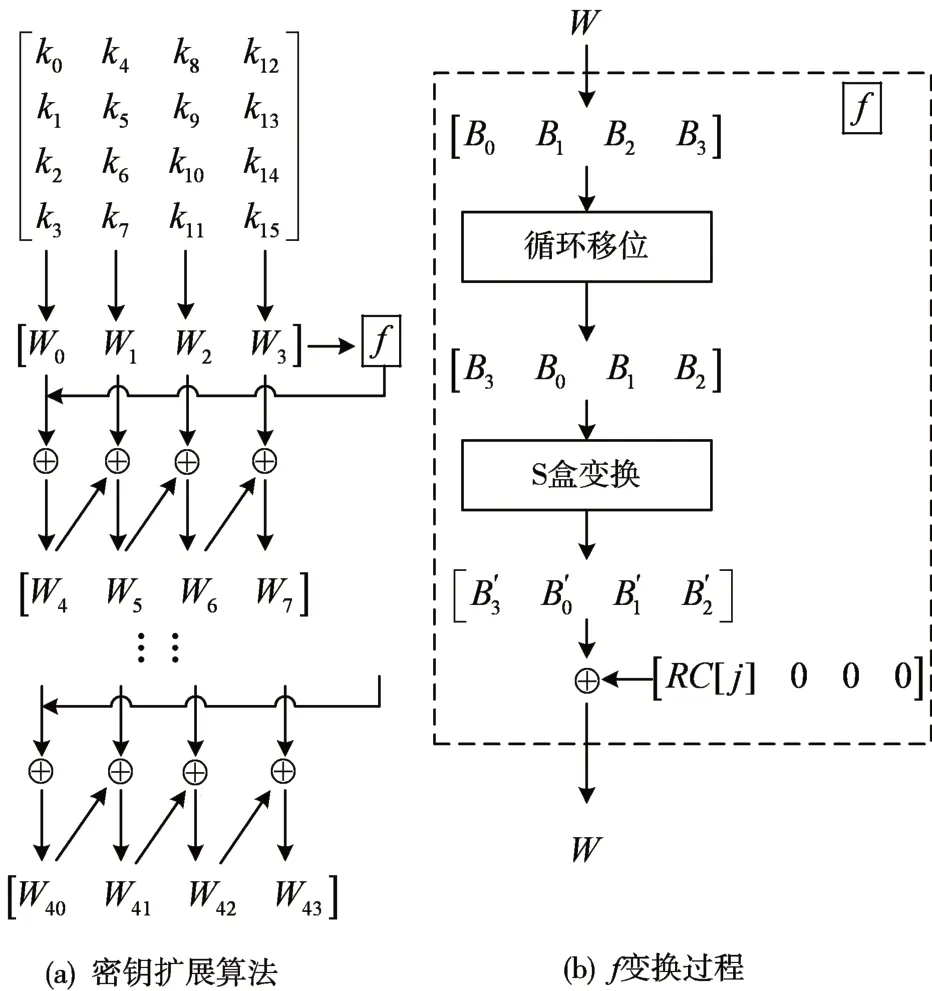
图2 密钥扩展流程图

根据i 数值不同，采用两种方法求解W[i]。当i 不是4 的倍数时，W[i]可以通过它之前的一个字与前面第四个字异或运算得到；当i 能够被4整除，W[i]的计算就比较复杂，需要对前面一个字进行f变换后再与前面第四个字异或运算得到。其中f变换包括以下三个步骤：

1）循环移位：对输入的W 向右循环移动一个字节。

2）S 盒变换：用S 盒替换步骤1）中的每个字节。

3）轮常量计算：将步骤2）的结果与常量Rcon[j]进行异或运算。 Rcon[j]代表一个字，定义Rcon[j]=(RC[j]，0，0，0)，这个字最右边三个字节始终为0。其中RC[1]=0x01，RC[j]=2*RC[j-1]。

2.2 AES加密过程

在加密过程中，需要加密的明文多数情况都会大于16 字节，所以需要对明文以16 个字节长度划分为若干段，以其中一段明文P 为例。假设第x轮的输入数据为状态矩阵Sx，密钥矩阵为Kx，其中x ∈[0，10]。初始的状态矩阵S0=P ，初始密钥为K0=(W[0]，W[1]，W[2]，W[3])，它们都是4*4的矩阵。加密流程［12］如下：

1）轮密钥加变换：S0⊕K0，⊕为异或运算。

2）S 盒变换：对Sx中的每个字节进行替换，而不改变原有的位置。AES 定义了一个由256 个字节组成的16*16 的表格——S 盒。在执行替换时，把该字节的高4位作为行值，低4位作为列值，找到S盒中对应的元素并取出代替该字节。

三要加快建设水资源配置和江河湖库水系连通工程，逐步构建“四横三纵、南北调配、东西互济”的水资源宏观配置格局，以及引排顺畅、蓄泄得当、丰枯调剂、多源互补、调控自如的江河湖库水网体系，强化水资源统一调度、科学调度。

3）行移位变换：对Sx的每行向左循环移动不同的位移量。第一行保持不变，第二行左移1 个字节，第三行左移2个字节，第四行左移3个字节。

4）列混合变换：将矩阵B 与Sx中的每一列相乘。以Sx中的一列为例，可表示成式（1）。之后将Sx的数据与对应的结果一一替换。

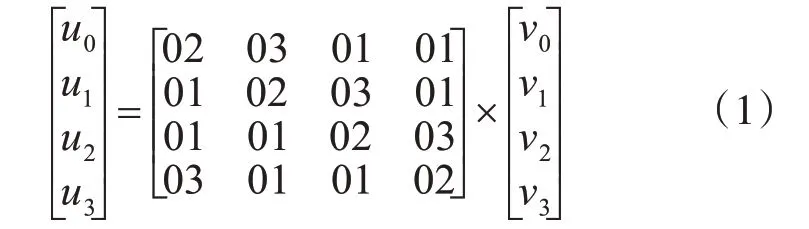
5）轮密钥加变换：将Sx中的每个字节与密钥扩展算法得到的Kx进行异或运算。

总共对步骤2）～步骤5）进行9 轮迭代循环，并在第10 轮运算时，舍弃列混合变换，最终得到的内容就是密文C 。

2.3 AES解密过程

AES的解密过程就是对加密的逆序。假设第x轮的输入数据为状态矩阵，密钥矩阵IKx，其中x ∈[0，10] 。初 始 的 数 据 为=C ，初 始 密 钥 为IK0=K10=(W[40]，W[41]，W[42]，W[43]) ，解 密 流程［13］如下：

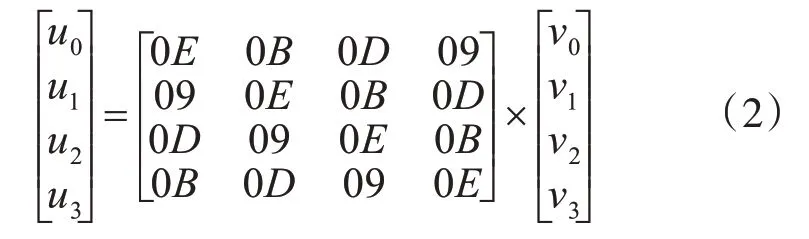
与加密过程不同，解密运算在第一轮时并不进行列混合逆变换，在第2～10轮时才进行完整的4种逆变换［14］。

3 AES算法优化设计

3.1 AES加解密过程复合优化

从图1 可以发现AES 的加解密过程并不是一个对称的结构，解密中变换的顺序与加密中的并不相同，所以在算法实现的过程中，通常都是将加密与解密模块独立分开。虽然这样做结构上比较清晰，实现也比较容易，但是其执行效率不高，也不适合一些存储资源受限的系统。为了能够将加解密过程中相似的模块进行复合，可以利用两条AES的性质进行优化［4］。

1）S盒变换与逆S盒变换只对输入字节进行非线性替换，并不更改其顺序。行移位变换与逆行移位变换只影响输入字节的顺序，并不更改其数值。

2）轮密钥加变换及其逆变换，列混合变换与它的逆变换都是线性变换。都有F(X+Y)=F(X)+F(Y)成立。

结合上述两条性质，可以调整加密过程中S 盒变换与行移位变换的顺序，再将解密过程中的逆列混合变换与轮密钥加逆变换调序。最终合并为一个整体，如图3 所示。经过调整后的AES 加解密过程完全共享一个迭代结构。与原来的AES 算法相比，该优化方法去除了一些加解密中重复性的实现过程，节省了存储空间，也为迭代中的变换提供了优化的基础。

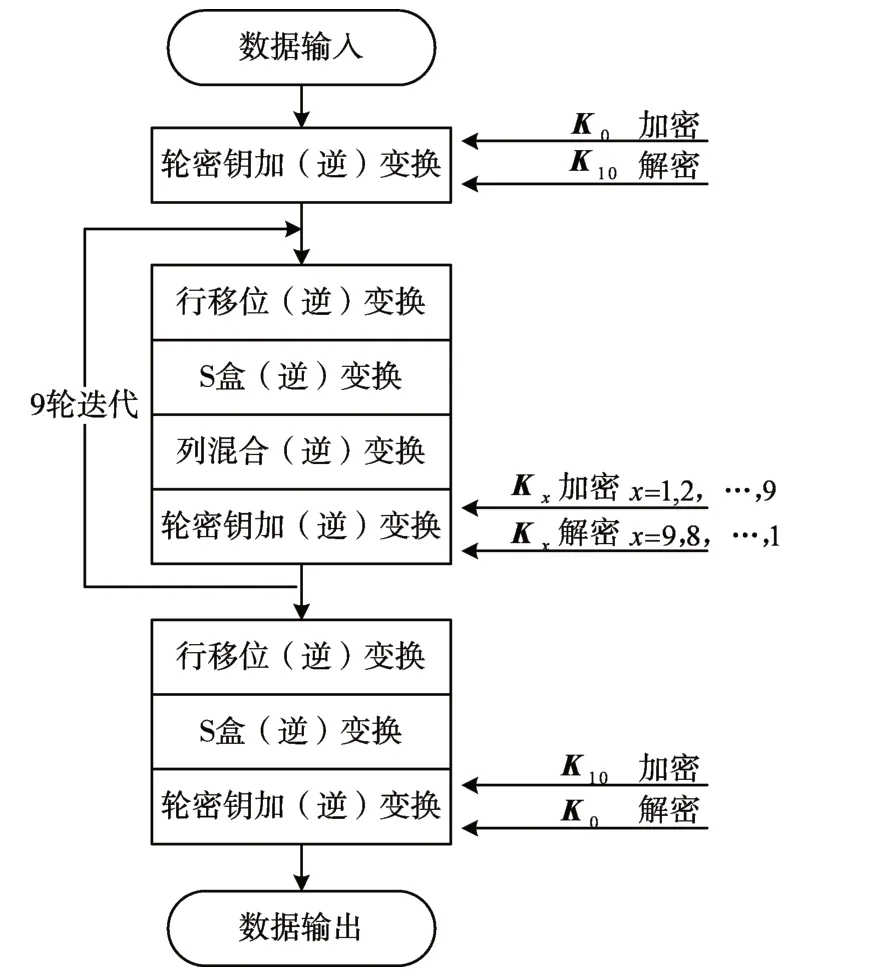
图3 调序合并后的加解密流程

3.2 S盒优化

S 盒作为AES 算法中唯一的一个非线性结构，在很大程度上决定了整个算法的安全强度。它的构造原理是先定义一个256 字节的表格，并按字节升序进行逐行排列，然后把表格中的每个字节映射到它在有限域GF(28)中的逆，最后经过仿射变换成为S盒。

传统的AES 中采用的仿射变换对为（F1，63），仿射变换的周期是4，并且迭代输出周期小于88。从数据安全性的角度考虑，S 盒的变换周期越大，数据才越安全，所以AES算法存在短周期现象［15～16］。针对这一现象，张丽红［7］提出了寻找最佳仿射变换对的优化思路，以严格雪崩准则为最终标准，找到了仿射变换周期为16，迭代输出周期为256的仿射变换对（34，BA）。本文引入这种新的S 盒构造方法，代替了传统的S 盒数据，从而提高了S 盒的性能，为其他优化方法打好了安全的基础。在软件实现上，可以通过查表法来减少运算的消耗。

3.3 行移位（逆）变换的优化

在行移位变换中，对状态矩阵的第n 行向左循环移动n-1 个字节；在行移位逆变换中，对状态矩阵的第n 行向右循环移动n-1 个字节。其中n ∈[1，4]。如图4 所示，（a）表示原始的状态矩阵，（b）表示行移位变换后的结果，（c）表示行移位逆变换的结果。

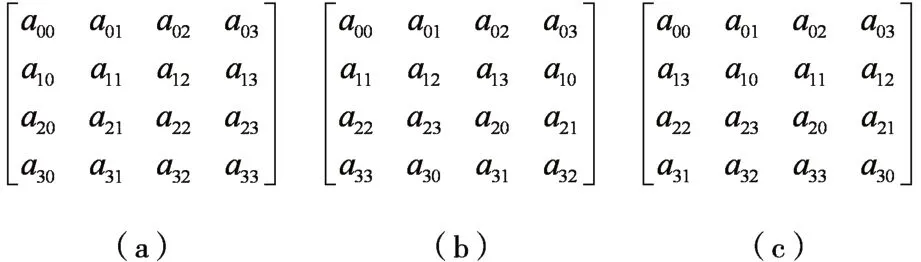
图4 行移位变换及逆变换结果

通过观察矩阵（b）和矩阵（c），可以发现第0 行与第2 行完全相同。所以这部分运算可以重合，流程如图5 所示，ML（n，n-1）表示第n 行左移n-1 个字节，MR（n，n-1）表示第n 行右移n-1个字节。

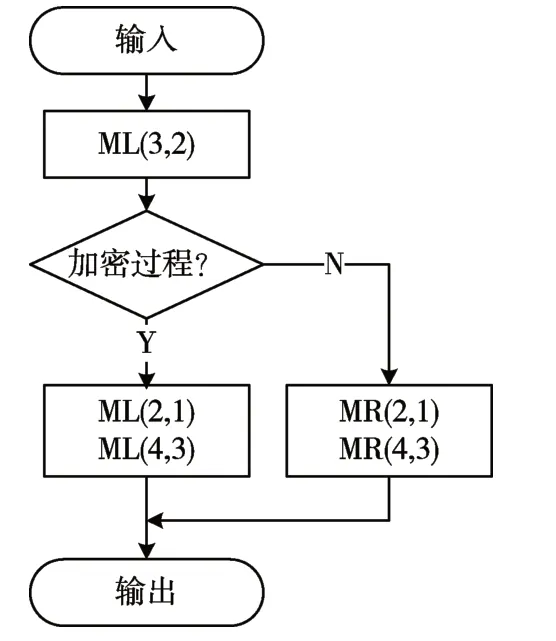
图5 行移位（逆）变换优化图

3.4 列混合（逆）变换的优化

结合等式（1）和（2），可以发现列混合变换比其逆变换所使用的矩阵简单的多。在软件实现上，列混合变换需要执行4次XOR运算和2次xtimes乘法运算；其逆变换则需要执行9 次XOR 运算和12 次xtimes乘法运算［6］。因为这两者的运算复杂程度的不同，导致加密与解密在时间消耗上存在一定的差距。所以在一些实时性要求高的情况下，这通常是不可接受的。针对这一问题，文献［4］提出将逆列混合变换的复杂矩阵分解成两个简单的矩阵，以此来提高运算的速度。但是这种方法实现比较复杂，效率提高不怎么明显。文献［5］应用了一种运算更为简单的矩阵A，并满足式（3）：

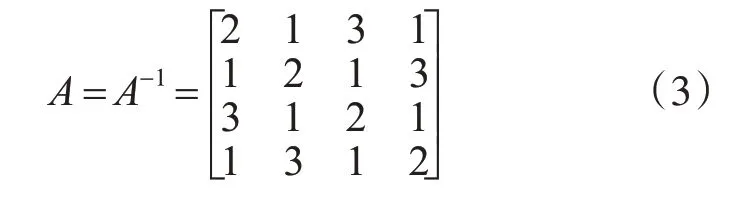
其特点是该矩阵在有限域GF(28)上的逆矩阵也是它本身。用此矩阵代替原算法中列混合变换及其逆变换的矩阵，可以使得它们消耗相同的计算资源并解决加解密过程中的时间不对称问题。另外，在软件实现上，相同的变换矩阵可以进一步合并这两种变换，可以有效地减少重复运算，降低存储资源的消耗，提升执行效率。

4 实验测试与分析

本文通过第3 节的四个优化措施，对原AES 算法进行了优化，为了验证改进后的算法效果，除了对执行效率进行测试之外，还对其安全性进行了实验分析。本次实验的硬件环境是STM32F103c8t6，工作主频是72MHz，有64KB Flash 和20KB SRAM，开发工具为Keil 5，算法的软件实现是通过C 语言编程。

4.1 安全性测试

检验密码算法是否满足雪崩效应是基本的安全性要求［7］。理想状态下，当任意改变输入的1 位时，平均有一半的输出位会发生改变。在分组密码算法中，雪崩效应的实现主要依靠扩散和混淆两部分，它们是影响密码安全的两个主要因素。扩散的目的是为了让密文中的多个信息受到明文中单个信息的影响，从而使得明文的统计特征在密文中消失。而混淆则是为了让密文与密钥之间的关系变得复杂化，使得破译方即时窃取了密文也无法推出密钥。下面通过实验来对比验证两种算法在雪崩效应方面的表现。

首先测试算法扩散性。为方便统计，任意选取一段16 字节长度的明文，使用原AES 算法和改进的算法进行加密。测试过程中，保证密钥不变，随机改变明文中的一位，记录密文变化的位数。实验结果如图6 所示，虽然原算法的平均密文变化位数是64，但是并不稳定，与优化后的算法相比，原算法波动范围比较大。

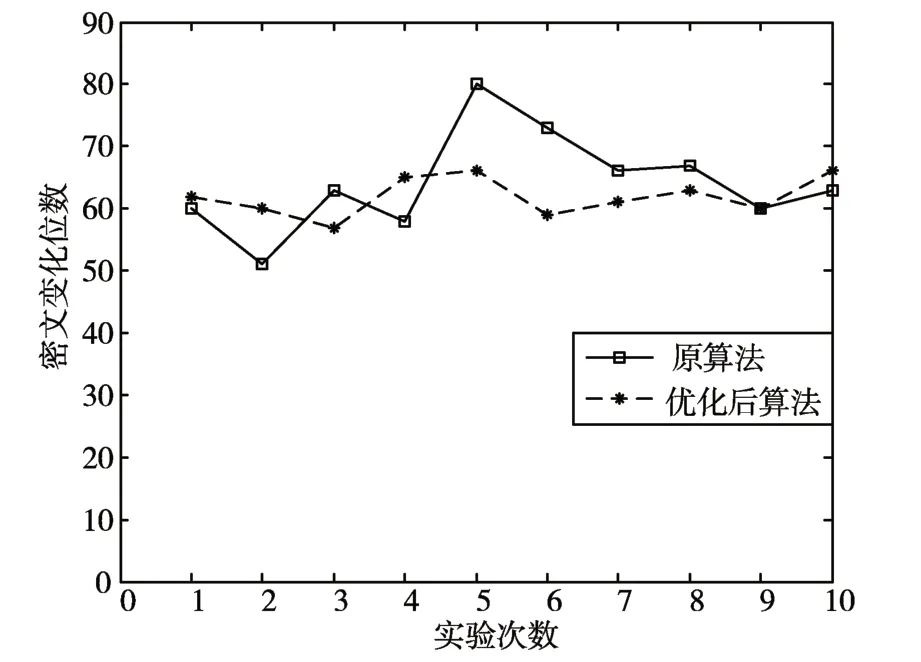
图6 扩散性测试结果

然后测试算法混淆性。同样任意选取一段16字节长度的明文，并保证其在测试过程中不变。记录密钥变化1位对密文的影响。实验结果如图7所示，原算法的密文改变位数的范围是61±9，改进后的密文改变位数的波动范围是62±5，波动范围显著缩小。

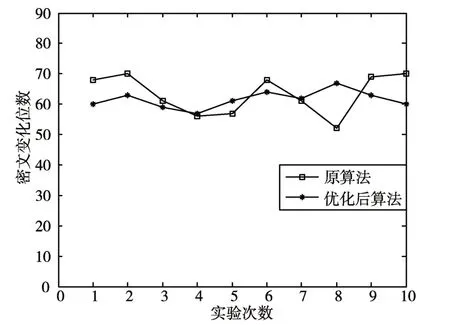
图7 混淆性测试结果

通过以上测试，可以发现改进后的算法在扩散和混淆方面有良好的表现，能够满足雪崩效应的基本要求，而且在安全性上有一定程度的提高。

4.2 执行效率测试

测试时，由于加密一个16 字节的字符串时间相当短，为了使实验效果更加明显，对5 组长度为100 字节的数据加解密各100 次，并记录其平均消耗的时间。实验结果如表3 所示。对表中的测试数据进行分析，改进的算法对加解密过程中的相似部分进行合并，使得改进后的算法在存储空间上比原AES算法节省了25%，列混合与逆列混合变换中采用简易矩阵，也使得加解密的耗时误差变小，决了原AES 算法中解密与加密的时间延迟问题。另外，在执行效率方面，改进后的加密速度比原算法提高了19%，解密速度比原算法提高了22%。这说明改进的算法较原算法有一定的优势。

表3 加解密耗时

5 结语

针对AES算法的不足之处，本文从安全性和执行效率两个角度对AES 算法进行了改进。采用新的高安全性S 盒可以增加被破译的难度；而对行移位变换和列混合变换的优化，也为加解密过程的整合降低了难度，提高了算法的执行速度。最终的实验结果也证实了改进算法在STM32 上运行具有一定的优势。下一阶段将在密钥管理方面做深入研究。