基于ITD与样本熵的汽车变速箱故障特征提取方法研究

刘国弟，赵伟杰，王树恒

（奇瑞汽车股份有限公司，安徽 芜湖 241000）

引言

汽车变速箱担负着传递发动机扭矩的作用，工作强度大，工况复杂，通过现代化手段，监测变速箱的运行状况，对预防故障具有重要意义。而在变速箱的故障诊断中，齿轮的故障诊断一直备受关注。由于齿轮在发生故障时齿轮结构的改变和齿轮的振动信号在传播时发生干扰和衰减，齿轮的振动信号往往具有强烈的非平稳特性。传统频谱处理方法有EMD分解，小波变换等。然而，EMD分解虽然有较好的自适应性，能较好的分析非线性和非平稳信号，但是也存在模态混叠和端点效应，计算复杂度较高，计算缺乏实时性等缺点；小波变换则缺乏对所处 理信号的自适应性。2006年，Frei提出的本征时间尺度分解（ITD）是一种新的非平稳信号分解方法[1]，该方法在提取信号的瞬时特征具有优异的性能，同时大大提高了计算效率，为齿轮箱的故障诊断提供了一种新的方法。

近年来，人们将熵的概念，作为特征参数提取的方法引入到故障诊断领域，包括排列熵、多尺度熵、模糊熵和近似熵等。样本熵（SampleEntropy，简称 SampEn）作为近似熵的改进算法，它比近似熵更少地依赖时间序列长度，效率更高[2]。本文将ITD方法与样本熵相结合，提出了一种基于ITD和样本熵的齿轮故障诊断方法，将齿轮故障振动信号进行ITD分解，将其分解为多个PR分量，再以样本熵方法定量描述含有故障主要信息的前几个 PR分量的复杂度，提取损伤特征，以实现对齿轮故障的诊断。

1 ITD方法

本征时间尺度分解能够自适应的将一个复杂信号分解成一系列互相独立的固有旋转分量（Proper Rotation，PR）和一个趋势分量之和[3]。对于原始信号Xt，定义L为其一个基线提取算子，如（1）式所示，从原始信号中去除基线后的余量作为原始信号的一个合理旋转分量PR。

式中：Lt=LXt表示基线信号；Ht为待提取的PR分量。

其分解过程为：

1）信号的基线提取算子Lt定义为：

式中，0＜a＜1，一般取a=0.5；Xk为原始信号的极值点；τk（k=1，2，…，M为极值点的个数）为极值点出现的时刻。

2 样本熵

样本熵是Richman在2000年提出的一种与近似熵相似，但又有别于近似熵的不计数自身匹配统计量，它相比近似熵拥有精度更高的时间序列复杂性[4]，其计算方法如下：

1）时间序列{x(i)}，（i=1，2，…N），由N个数据组成，x(i)为第i个数据。将{x(i)}构造成m维矢量。

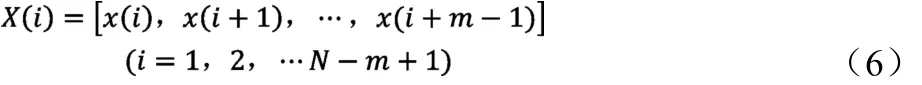
2）向量X(i)和X(j)之间的距离定义为d（i，j），它为两向量相对应元素最大差值的绝对值，

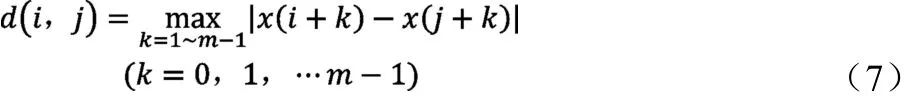
3）对每个i，其对应向量x(i)与其他向量x(j)（j=1，2，…N-m；j≠i）之间的距离为d（i，j），统计d（i，j）＜r 的数目，此数目与距离总数N-m+1的比值记作（i=1，2，…N-m）。

4）定义B(m)(r)为：

5）将维数再增加 1，然后重复上述步骤 1）～4），得到，再进一步得到。

6）则此序列在理论上的样本熵为：

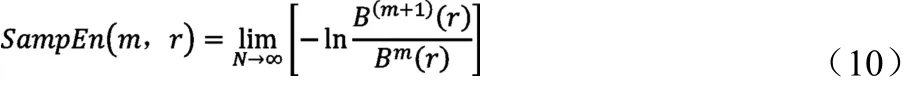
当N为有限值时，则此时的样本熵估计值为：

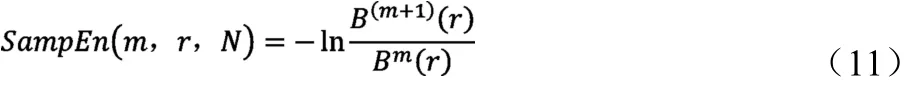
可以看出，样本熵的值显然与嵌入维数m，相似容限r相关，因此确定m、r这两个参数的值，对于样本熵的计算起到非常重要的作用。由文献[5]的研究结果得知，在m=1或2，r=0.1Std～0.25Std（Std为原始数据x(i)标准差，i=1，2，…N），此时计算所得的样本熵具有比较合理的统计特性。在本文中取m=2，r=0.2Std。

构造样本熵的仿真信号，信号如下：

采样频率定为 4000Hz，采样时间为 1s，样本熵的嵌入维数m=2，相似容限r=0.2Std，计算样本熵长度N=100的子序列为一个采样长度，然后依次把采样长度向后推移一个点，一直要第3900点为止，相当于是把原始的信号分解为40个部分，得到的40个部分子信号样本熵如图1所示。

在图中可以清晰地看到仿真信号的样本熵发生了4次明显的变化，而样本熵突变的时刻正好对应了其仿真信号的 4次频率突变，并且信号频率越大的地方，其所对应的样本熵也越大，因此，样本熵的变化是可以反映其原始信号的频率变化及信号的复杂度情况的。由这个思路，可以把原始信号进行ITD分解，再把最终得到的PR分量来当作样本熵的输入序列来计算其在不同的状态下样本熵的大小。

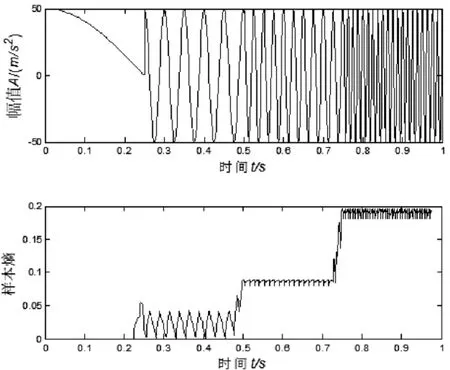
图1 样本熵仿真图

3 ITD-样本熵试验

本次实验采用的是美国Spectra Quest公司生产的可模拟变速箱故障诊断综合实验台（WTDS）。该试验台主要由二级行星轴承箱、由轴承支撑的二级平行轴轴承箱、轴承径向负载和可编程磁力制动器等部分组成。实验通过更换齿轮来实现输入轴上的直齿小齿轮的正常、齿根裂纹、断齿和缺齿四种状态，传感器类型为电涡流加速度传感器。电机的转速分别为1800rpm，采样频率为7680Hz，采样点数为4096。

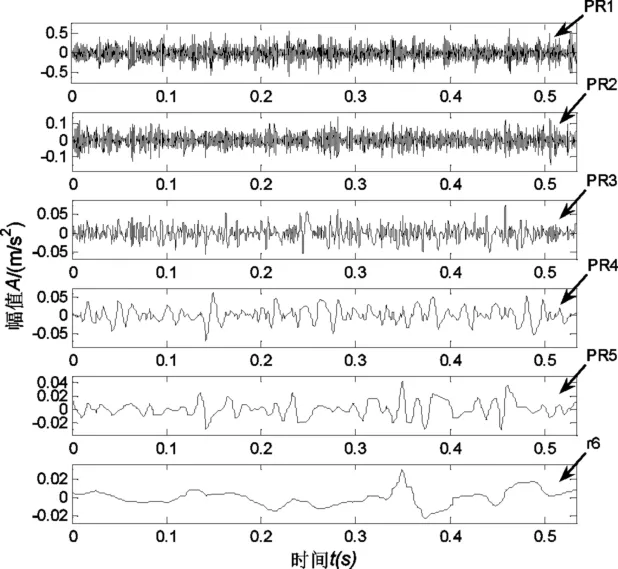
图2 断齿齿轮信号ITD分解

图2为缺齿振动信号的ITD分解图，可看出振动信号被分解成5个PR分量以及一个趋势项，由于PR1和PR2分量和原信号的相关系数远高于其他分量，因此选取PR1和PR2的样本熵作为齿轮各状态计算和比较的对象。

选取嵌入维数m=2，相似容限r=0.2Std，计算齿轮四种状态的ITD-样本熵值，且每次只计算PR1和PR2两个分量的样本熵值。

图3是对齿轮的四种状态用ITD-样本熵方法得到的熵值图。在图中可以看出，四种状态下ITD-样本熵值大小关系呈现为正常＞齿根裂纹＞断齿＞缺齿。而且PR2分量的ITD-样本熵图都要比PR1的平缓，这是因为ITD分解层数越大，则其分量复杂度就会迅速降低，信号就变得越来越简单。观察齿轮四种不同状态下信号的ITD-样本熵图，会发现齿轮正常状态下分量的样本熵会大于其他三种状态。这是因为在齿轮正常工作状态下信号的随机性和复杂度更高。齿根裂纹的ITD-样本熵和正常状态下相差不大，这是因为齿根裂纹的故障特征不是特别明显，齿轮仍然可以继续工作，周期性冲击较弱。缺齿的ITD-样本熵最小，这是因为缺齿产生明显的周期性冲击，这些冲击大大降低了原始信号的随机成分，令信号的自相似变大，所以其样本熵会明显降低。

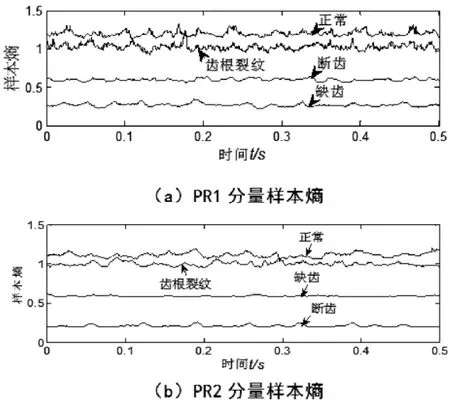
图3 不同状态的ITD-样本熵图

4 结论

（1）样本熵可以很好的反映出齿轮出现故障时其振动信号的变化，并且齿轮在不同状态下的ITD-样本熵不相同，说明样本熵可以作为齿轮故障诊断的特征。

（2）ITD分解可以把信号分解成一系列的 PR旋转分量，分解的过程其实是去噪的过程，因为噪声的随机性会对ITD-样本熵的结果产生很大的干扰。而前两个分量和原信号的相关系数远高于其他分量，它们的样本熵值更具有说服力。