不同势能模型下的水分子动力学性质

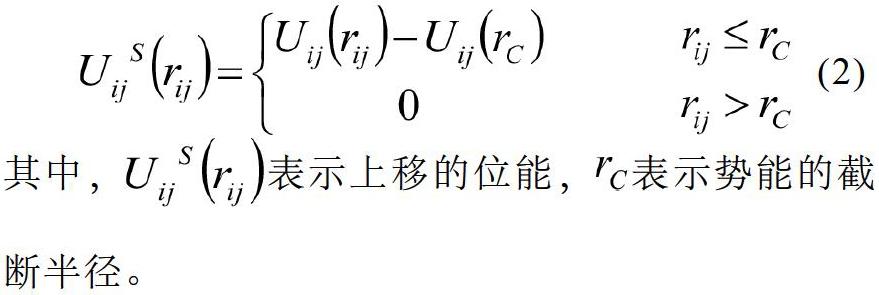
摘   要： 采用分子动力学方法，对SPC、SPCE、TIP3P、TIP4P、TIP5P五种势能模型下水分子的热力学性质、径向分布函数、自扩散系数进行计算，优选最适合于水分子动力学性质研究的势能模型。研究发现：1）采用SPCE模型通过模拟得到的内能、汽化焓最为准确，其他模型受到了模型固有性质和系综（大量宏观上完全相同的体系的抽象集合）的影响，模拟结果不甚理想;2）采用SPCE、TIP4P、TIP5P模型可以较好地反映水分子短程有序、长程无序的微观结构;3）采用SPCE模型通过模拟得到的自扩散系数相对误差仅为0.39%，远好于其他模型。结果表明，SPCE模型能够较真实地反映水分子的热力学性质、微观结构和自扩散特性等动力学性质。

关键词： 水分子;势能模型;动力学;径向分布函数;自扩散系数

中图分类号：O645    文献标识码：A    文章编号：2095-8412 （2020） 05-085-05

工业技术创新 URL： http：//gyjs.cbpt.cnki.net    DOI： 10.14103/j.issn.2095-8412.2020.05.016

引言

水是生命的源泉，水分子的研究對水的开发利用具有非常重要的意义。分子动力学（MD）方法是模拟水分子动力学性质的一种非常有效的方法，一直受到国内外研究者的关注[1-3]。

单个水分子看似结构比较简单，但氢键的作用使得水分子相互聚合，形成多分子聚合物，水分子的微观结构发生了复杂化。采用分子动力学方法研究水分子，最重要的也是选择分子间的相互作用势。在水分子动力学计算中，可以选择多种势能模型，包括量子力学从头计算模型（如MCY模型[4]）、半经验模型（如ST2、SPC、SPCE、TIP3P、TIP4P、TIP5P）等[5-8]。MCY模型结构较为复杂，计算时间成本较高，因此在实际应用中更多采用半经验模型。

本文对水分子的SPC、SPCE、TIP3P、TIP4P、TIP5P等势能模型进行计算，考察水分子的热力学性质、径向分布函数、自扩散系数，优选最适合于水分子动力学性质研究的势能模型。

1  势能模型

SPC、SPCE、TIP3P、TIP4P、TIP5P这几种模型都是刚体固定点电荷模型，计算时选用非极性作用Lennard-Jones势模，分布为有效电荷表征电子云。

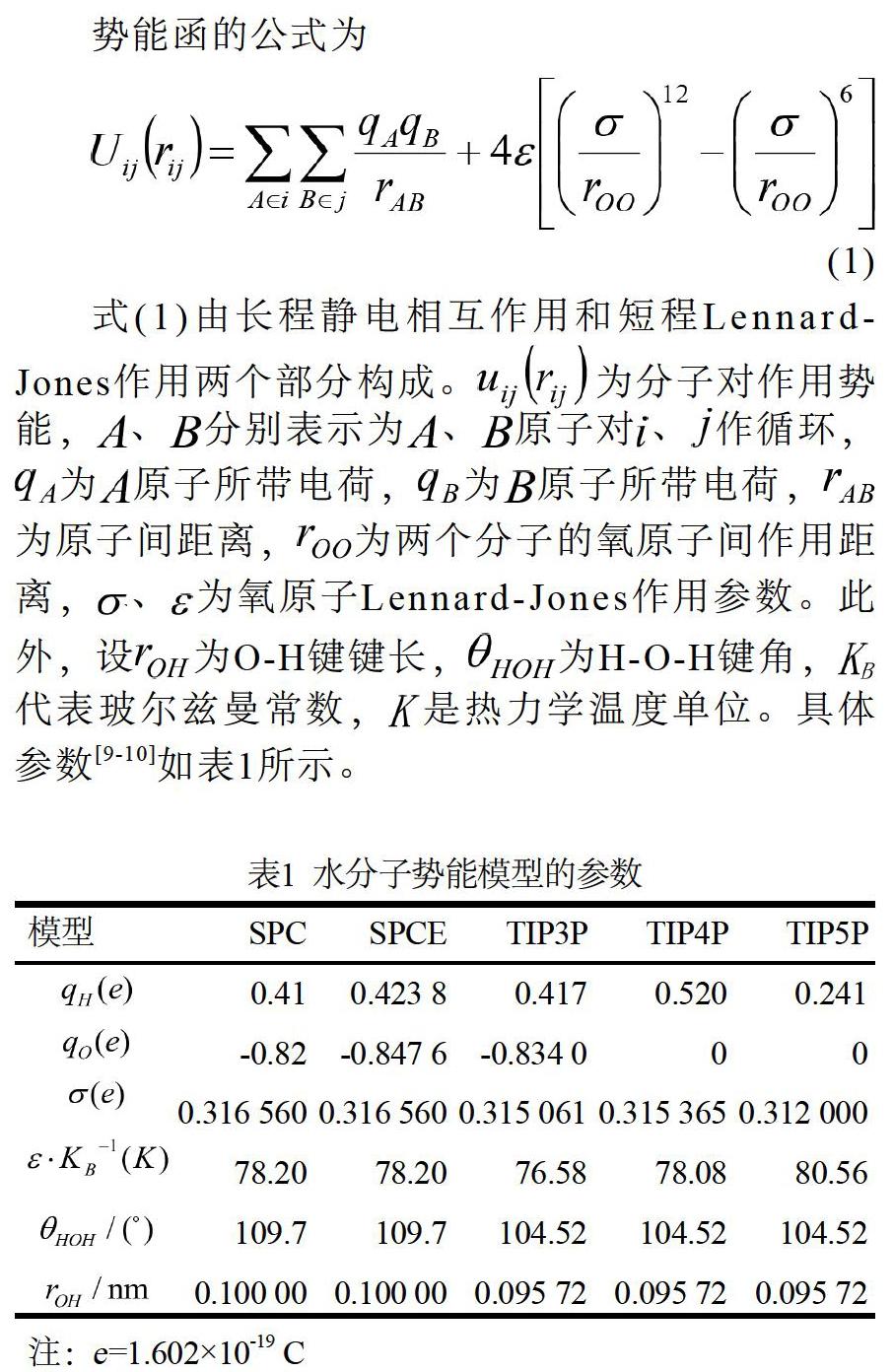
势能函的公式为

式（1）由长程静电相互作用和短程Lennard-Jones作用两个部分构成。为分子对作用势能，、分别表示为、原子对、作循环，为原子所带电荷，为原子所带电荷，为原子间距离，为两个分子的氧原子间作用距离，、为氧原子Lennard-Jones作用参数。此外，设为O-H键键长，为H-O-H键角，代表玻尔兹曼常数，是热力学温度单位。具体参数[9-10]如表1所示。

势能的截断，会使计算时能量在边界处发生断裂，导致哈密顿函数不守恒。采用上移的势能函数[7]来弥补缺陷，计算公式为

其中，表示上移的位能，表示势能的截断半径。

2  模拟方法

模拟的水分子总数为300个，模拟温度为298 K、压强为1 atm（常温常压），模拟系综（系综表示大量宏观上完全相同的体系的抽象集合）为正则系综（NVT），水的起始密度设为1.0 g/cm3。

计算模型设为面心立方晶格，计算开始时水分子取向随机，各分子的起始速度按Maxwell-Boltzmann分布取样，对温度的控制采用速度标定法，以确保体系总动量为零。

计算过程中采用最小镜像准则和两体有效势基本近似，周期性边界条件采用立方结构[11]，计算盒子尺寸由密度确定。采用球形截去法，设置截断半径为0.9 nm。采用长程校正法校正截断半径之外的分子间相互作用能，长程静电相互作用采用Ewald加和法[12]进行计算。

几何构型的固定采用SHAKE算法，采用5阶Gear预估—校正法[13]求解运动方程。计算时所取时间步长为2 fs，每次模拟总时间为300 ps，前200 ps使体系达到平衡，后100 ps用于进行统计计算各种物理性质。

3  结果与讨论

3.1  热力学性质

计算常温常压下，不同势能模型下水的内能、汽化焓，并把所得结果与实验值和其他文献值进行比较。

汽化焓计算公式为

其中，H表示焓值，E代表体系内能，P是压强，V是体积，T是温度，R是普适气体常量。

模拟结果与比较如表2所示，其中MC代表量子力学从头计算模型。选用SPCE模型模拟得到的水的内能、汽化焓与实验值和其他文献值较接近，而其他模型可能受到了模型固有性质和系综的影响，模拟结果不太理想。总之，采用SPCE模型计算水分子的热力学性质最为合适。

3.2  径向分布函数

径向分布函数是反映流体微观结构的物理量，它表明了与某个原子距离为的单位体积元内出现的分子数，表达式为

其中，为体系的体积，为分子数，为两个分子的质心的距离，为函数。

计算常温常压下水分子在不同势能模型下的gOO（O-O径向分布）、gHO（H-O径向分布）、gHH（H-H径向分布），并与实验值[12]进行比较。

图1a所示为O-O径向分布函数与实验值。可以看出，不同势能模型的O-O径向分布函数与实验值的峰值变化趋势都相符，其中SPCE、TIP4P和TIP5P三个模型与实验值一样出现了三个峰值，SPC、TIP3P只有一个峰值。综合来看，在研究水的O-O径向分布函数时，选用TIP5P模型更为合适。此外，SPCE、TIP4P和TIP5P模型的第二峰值出现在0.45 nm，第三峰值出现在0.68 nm，这与文献[15]使用蒙特卡罗方法所得结果相一致。

圖1b所示为H-O径向分布函数与实验值。比较不同模型的峰值出现的位置，出现第一峰值和第二峰值的位置与实验值相吻合，第一峰值的出现是氢原子与氧原子形成的共价键产生的结果。

图1c所示为H-H径向分布函数与实验值。观察第一峰值的峰位和第二峰值的峰位，其分别反映的是中心水分子与近临水分子、第二配位圈水分子间的H-H距离。SPC和TIP3P模型的H-H径向分布函数与实验值吻合得不太理想，其他模型的模拟均与实验值吻合的较好。

综合分析径向分布函数，可以发现随着r的增加，函数趋于缓和，这种现象反映了水分子短程有序、长程无序的微观结构特征。综上所述，选用SPCE、TIP4P和TIP5P三种势能模型可以较好地反映出水分子的微观结构。

3.3  自扩散系数

可以用两种方法计算自扩散系数，一种是对均方位移（Mean Square Displacement，简称MSD）求斜率的Einstein方法[12]，另一种是对速度自相关函数求积分的Green-Kubo方法。Einstein方法的公式为

其中，为水分子的质量，为玻尔兹曼常数，为体系的温度，、分别为0时刻和时刻粒子的速度。

采用以上两种方法分别计算水的自扩散系数。图2所示采用Einstein方法为不同模型计算的均方位移。可以看出均方位移斜率由小到大分别对应SPCE、TIP5P、TIP4P、SPC和TIP3P模型，表明自扩散系数也依次增大。

表3给出了采用两种方法计算的自扩散系数与其他文献[17]所得结果及实验值[18]的比较。可以看出，采用Einstein方法计算的自扩散系数要比Green-Kubo方法更为理想，所得结果比文献[17]的值更符合实验值。采用Einstein方法计算所得结果比Green-Kubo方法小，这与速度自相关函数的积分区间选取有关，从而导致了松弛时间的差异，即当速度自相关函数从1突降到0附近后，一直在0附近保持振荡，这表明此后粒子的速度与时间不再相关。松弛时间一般很难准确确定，这将会影响到自扩散系数积分区间的选取。SPCE模型得到的结果与实验值最接近，相对误差仅为0.39%。TIP5P模拟结果次之，相对误差为13.87%，但比SPC、TIP3P、TIP4P模拟结果要好得多。在TIP3P模型中，两种方法得到的结果与实验值相差最大，分析其原因可能是此模型下氢氧有效电荷数相差较大，使得氧原子束缚了氢原子。SPC和TIP4P计算结果也与实验值相差较大，但是相比文献[17]要好得多。

4  结束语

势能模型的选取是分子动力学计算的关键。本文采用分子动力学方法计算了五个势能模型下水分子的内能、汽化焓、径向分布函数及自扩散系数。

综合分析发现，SPCE模型最适用于水分子动力学性质的研究，能够较真实地反映水分子的热力学性质、微观结构和自扩散特性，值得学者广泛关注。

基金项目

教育后勤疫情防控专项课题（课题编号：ZXYBKT202022）

参考文献

[1] Alder B J， Wainwright T E. Phase Transition for a Hard Sphere System[J]. Journal of Chemical Physics， 1957， 27（5）： 1208-1209.

[2] Rahman A. Correlations in the Motion of Atoms in Liquid Argon[J]. Physical Review， 1964， 136（2）： 405-411.

[3] Cheung P S Y， Powles J G. The properties of liquid nitrogen. IV. A computer simulation[J]. Molecular Physics， 1975， 30： 921-949.

[4] Matsuoka O， Clementi E， Yoshimine M. CI study of the water dimer potential surface[J]. Journal of Chemical Physics， 1976， 64（4）： 1351-1361.

[5] Stilliger F H， Rahman A. Improved simulation of liquid water by molecular dynamics[J]. Journal of Chemical Physics， 1974， 60（4）： 1545-1557.

[6] Berendsen H J C， Postma J P M， Gunsteren W F， et al. Intermolecular Forces[M]. Holland： D. Reidel Publishing Company， 1981： 331.

[7] Berendsen H J C， Grigena J R， Straatsma T P. The missing term in effective pair potentials[J]. J Journal of Physical Chemistry， 1987， 91（24）： 6269-6271.

[8] Mahoney M W， Jorgensen W L. A five-five model for liquid water and the reproduction of the density anomaly by rigid， nonpolarizable potential functions[J]. Journal of Chemical Physics， 2000， 112（20）： 8910-8922.

[9] 李印实， 何雅玲， 孙杰， 等. 不同水分子模型凝结系数的分子动力学对比研究[J]. 西安交通大学学报， 2006， 40（11）： 1272-1275.

[10] Mills R. Self-diffusion in normal and heavy water in the range 1-45.deg[J]. Journal of Physical Chemistry， 1973， 77（5）： 685-688.

[11] Allen M P， Tildesley D J. Computer Simulation of liquids[M]. Oxford： Clareendon Press， 1987.

[12] De Leeuw S W， Perram J W， Smith E R. Simulation of electrostatic systems in periodic boundary conditions. I. Lattice sums and dielectric constant[C]// Proceedings of the Royal Society A， 1980， 373： 27-56.

[13] Gear C W. Numerical Integration of Ordinary Differential Equations[M]. New Jersey： Prentice Hill， 1971.

[14] Soper A K， Phillips M G. A new determination of the structure of water at 25℃[J]. Chemical Physics， 1986， 107（11）： 47-60.

[15] 吴熊武， 腾藤， 李以圭， 等. 水—甲醇体系的Monte Carlo分子动力學模拟[J]. 化学学报， 1992， 50： 543-548.

[16] Krynicki K， Green C D， Sawyer D W. Pressure and temperature dependence of self-diffusion in water[J]. Faraday Discussions of the Chemical Society， 1978， 66： 199-208.

[17] Jorgensen W L， Jenson C. Temperature Dependence of TIP3P， SPC， and TIP4P Water from NPT Monte Carlo Simulations： Seeking Temperatures of Maximum Density[J]. Journal of Computational Chemistry， 1998， 19（10）： 1179-1186.

[18] 刘娟芳， 曾丹苓， 蔡智勇， 等. 扩散系数的分子动力学模拟[M]. 工程热物理学报， 2006， 27（3）： 373-375.

作者简介：

俞联梦（1983—），通信作者，女，云南大理人，硕士研究生，讲师，从事高校教学工作。主要研究方向：分子动力学。

E-mail： 175365186@qq.com

（收稿日期：2020-06-18）