基于智能算法的桥梁结构边界特性识别
梅 冲,周 杰,杜震超
(武汉轻工工程技术有限公司,武汉 430073)
桥梁结构的精确有限元模拟可以为桥梁设计、监测、加固决策提供可靠依据,在采用有限元程序对桥梁结构进行模拟时,桥梁支座的刚度直接影响结构在静载下的位移响应[1,2]。然而,由于支座安放角度、施工质量、产品规格变异以及长时间服役后橡胶的老化、盆式支座的磨损等原因,直接采用支座生产厂家提供的数据建立有限元模型的约束,会存在一定的误差,特别是在潮湿、严寒、高温等易加快橡胶老化的环境下,支座对梁体的约束情况与出厂时可能存在较大误差[3]。
如何准确模拟结构的实际边界条件,为结构的设计、运维提供可靠依据已经成为近年来工程界的迫切需求,也逐渐转化为学术界的研究热点[4]。
其中一种可行的方案是,根据结构在实际荷载下的位移响应,反演结构的边界约束情况[5-7]。在静载作用下,结构发生的位移由两部分组成:支座的弹性形变和结构本身的受力形变,而结构的形变与支座情况相同,在长时间服役后会出现结构变异,从而影响结构的位移响应。因此结构在静载下发生位移时,如何判别位移成为研究难点。
为解决上述问题,采用智能优化算法,根据结构在静载下的位移响应,反演结构的变异和支座的边界特性。并且以一个箱梁单梁为案例,分析了该文推荐的算法及识别流程,然后采用所述方法对其进行了优化,对比了优化前后的支座刚度以及结构的位移响应差值。
1 桥梁结构边界特性识别原理
1.1 结构反演原理
根据结构的实际参数,如尺寸、物理性能(弹性模量密度)等,计算结构在荷载下的静动力响应,属于结构计算的正问题。而根据结构在已知荷载下的响应,反算结构的物理参数、尺寸等信息,属于结构反演。在确定性模型中,结构能够进行反演的基本假设是在确定荷载下,每组结构参数都存在一个且唯一的响应。
通过一定算法不断调整结构的设计参数,使之响应与测得响应相一致的过程称为结构参数识别。
准确识别结构边界条件,对结构的后期运维至关重要。为得到精确的结构支撑刚度,提出了利用遗传算法,采用反演方法分析结构边界条件的流程,并在实际案例上进行了验证。结果表明,智能算法配合反演的方法可以准确识别结构边界刚度,为结构的运营维护提供了参考。
1.2 结构参数反演流程
结构参数识别的一般步骤是:
1)根据设计图纸确定初始结构参数,并根据该组参数建立有限元模型;
2)对实际结构进行静动力响应测试;
3)根据测试结果采用优化算法调整设计参数,计算在新参数下的结构响应;
4)根据优化参数下结构响应与结构实际响应的差值,根据算法设定的准则确定下一组优化参数;
5)运行步骤4直至满足算法终止条件。
该文选择的终止条件为算法迭代次数达到上限。
2 遗传算法
遗传算法是一种群智能算法,受启发于自然界中生物进化过程。在微观层面,生物基因经过复制、交叉、变异等过程,从而在宏观层面表现出个体逐渐适应环境和优胜劣汰的行为。

遗传算法[8-10]模拟生物界进化过程,问题的一个可行(不一定是最优)解对应一个个体,问题自变量的维度对应个体基因中染色体的条数。每条染色体上有很多基因点位,整个基因确定了个体所处位置,而个体在评价函数中的位置确定了其适应性大小。
遗传算法的步骤:
1)根据实际问题初始化一群个体,个体数量,个体的维度等信息;
2)计算每个个体的适应度,根据适应度对个体进行排序;
3)复制一定比例的个体作为父代;
4)父代与所有个体随机匹配然后交换一组或多组染色体,形成子代;
5)对部分子代或父代的随机个别基因点位进行变异;
6)计算所有父代子代的适应度,并采用轮盘赌等法则选择合适的子代;
7)判断子代的适应度是否满足迭代终止条件,是则退出循环,输出结果,否则进入步骤2进行下一步迭代计算,直至满足迭代终止条件,见图1。
3 案例分析
为验证所提算法的可行性,以一个简直梁为背景,以边界特性参数和梁体刚度为识别变量,采用遗传算法对结构参数进行识别,结构的概况为:结构为30 m跨径单梁,截面形式为箱型,箱梁毛截面几何特性见表1,尺寸见图2。


表1 箱梁毛截面几何特性
结构材料:
1)混凝土:预制梁及现浇湿接缝、横梁为C50、现浇调平层为C40。
2)预应力钢绞线:采用钢绞线φs15.2,fpk=1 860 MPa,Ep=1.95×105MPa。
3)普通钢筋:采用HRB335,fsk=335 MPa,ES=2.0×105MPa。
实验:
为验证结构在荷载下的受力性能,对其进行了静载实验。依据相关规范,本次试验对梁体的L/2跨(A-A截面)和L/4跨(B-B)各布置9个应变测点和3个挠度测点,各截面测点布置如图3所示。

由于条件限制,无法在支座处安装位移计,因此,无法直接判断结构支座的位移。
对主梁施加荷载,梁体产生的位移如表2所示。

表2 结构实测位移值
梁中部测得的挠度由两部分组成:梁在荷载下的变形和支座的位移。由于结构混凝土的碳化等原因,根据设计图纸直接采用有限元计算的位移与实际位移存在差异。因此需要将结构材料弹性模量和支座刚度同时作为变量进行优化。
参数识别:
根据设计图纸,并采用参数化建模方法建立初始有限元模型,采用梁单元对结构进行模拟。通过不断调用有限元程序改变模型弹性支撑刚度和材料弹性模量来逼近结构真实位移。
在优化算法中,需要设定一个参数来衡量有限元模拟响应与真实响应之间的吻合程度。采用的位移差值向量的2-范数,如下式所示
E=|Dfe-De|2
式中,E为目标函数值;Dfe为结构有限元模型计算的位移向量;De为结构在实际荷载下测得的位移向量。
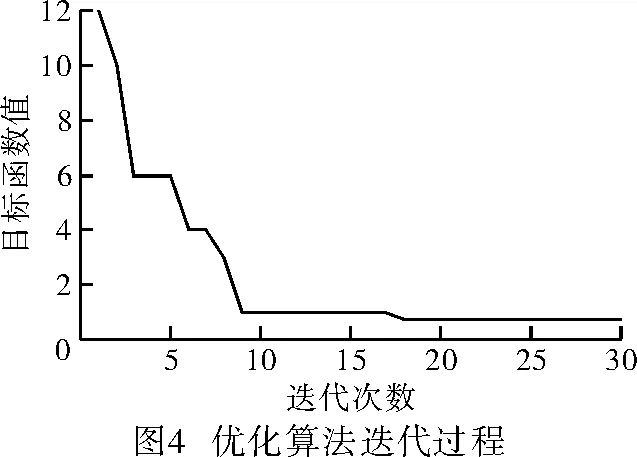
采用遗传算法对目标函数进行寻优,寻优过程如图4所示。
从图中可以看出,算法优化速度较快,在18次后不再进化,认为寻找到了目标函数的最优解。
最优解为支座刚度K=882 000 kN/m,混凝土相对弹性模型为0.97(在优化程序中,为便于计算,将优化弹性模量与初始弹性模量的比值作为优化变量)。优化结果如表3所示。
从表3中可以看出,优化后3点的位移值均有较大幅度的减小,且最终的误差小于1%。表明优化结果的弹性模量和刚度具有较高精度。弹性模型经过优化后,有小幅度减小,可能原因是经过长时间环境作用,混凝土出现了一定程度的碳化。

表3 优化结果对比
4 结 论
结构边界特性的精确模拟至关重要,通过反演与群智能算法相结合的方式,对一个箱梁支座刚度以及结构的弹性模型进行了联合反演。在未优化前,结构初始有限元模型的计算结果和实测结果之间的差值达到了11%以上,通过遗传算法的优化,三处的结构位移误差均降到了1%以下,提高了有限元的拟合精度,研究可为有限元的精确模拟提供参考。

