变马赫数下压力面小翼对扩压叶栅气动特性的影响
吴宛洋,钟兢军
(上海海事大学 商船学院,上海 201306)
叶尖小翼技术最早的设计概念来自于自然界飞禽类的翅膀结构特征. 早在1897年,飞机面世前,英国的空气动力学家兰彻斯特就首次提出在翼尖处加装端板结构以改善空气动力学特性的影响,可惜由于早期航空技术及工业的限制,兰彻斯特提出的翼梢小翼的设计理念无法付诸实现. 一直到1976年,美国NASA研究中心的惠特科姆博士[1]才真正的通过实验证明了翼稍小翼在改善飞机航行状况的有效性,接着在风力机[2]、螺旋桨[3]、轴流风机[4]及涡轮[5]等多种叶轮机械领域叶尖小翼都被证明是一种有效的叶顶泄漏流动的控制手段. 压气机叶片厚度较小,流场中流动更为复杂,各种涡系的存在对流场的影响更为明显,因此在压气机中应用叶尖小翼技术的研究开展较晚. 国内钟兢军团队[6-8]自2008年开始对叶尖小翼在压气机中的应用开展了大量的研究,经过多年的理论分析、数值计算及实验测量初步确定了在低速来流条件下合适安装位置及结构参数的叶尖小翼可以有效地控制叶顶泄漏流动的运行轨迹,延迟泄漏流动与主流的掺混,减小叶栅中总压损失,而在跨声速转子中,压力面叶尖小翼则可以通过改变泄漏涡的流动轨迹有效提高压气机转子的稳定工作范围.
由于叶尖小翼对跨声速流场的影响效果受到多种因素的共同影响,如:叶型、来流马赫数、冲角、进口附面层以及间隙高度等,因此不同的学者们得到的结论不尽相同,吕和斌[9]以某扩压叶栅为研究对象,利用数值计算对跨声速来流条件下叶尖小翼对流场的影响进行了研究,结果发现吸力面叶尖小翼削弱了流场中泄漏涡的强度,降低了流场中总压损失. 牛汗[10]对某跨声速转子进行了叶尖小翼安装后流场的数值计算,结果发现当压力面叶尖小翼的宽度为4倍叶顶截面宽度时,压气机转子的流量裕度可增加24.5%. Shivaramaiah[11]针对某跨声速转子中加装不同宽度的压力面叶尖小翼和吸力面叶尖小翼对流场的影响进行了研究,结果证明吸力面叶尖小翼的性能优于压力面叶尖小翼和组合小翼.
现有研究成果主要以低速叶栅和跨声速压气机转子为研究对象,在高亚声速领域还存在空白,同时现有文献资料证明叶尖小翼技术的适用性受到多种因素的共同影响,来流马赫数的变化必然会引起控制机理上的改变,探究高亚声速下叶尖小翼控制压气机叶栅叶顶间隙流动的工作将为实际工况中最佳叶尖小翼的选择提供参考. 本文对来流马赫数分别为Ma=0.5、Ma=0.6和Ma=0.7的3个工况下原型叶栅和加装不同宽度压力面叶尖小翼的扩压叶栅的流场进行了实验研究,并对测量结果进行对比分析,探究来流马赫数的变化对压力面叶尖小翼间隙泄漏控制效果的影响,为高亚声速下叶尖小翼在压气机中的实际应用提供理论依据.
1 实验装置介绍
1.1 实验叶栅设计
研究过程的实验测量在大连海事大学船用小型燃气轮机技术重点实验室的高速平面风洞完成,实验探针为L形五孔探针. 叶栅叶型为GE某转子叶顶的截面,叶型为了满足实验风洞的尺寸要求,将叶型尺寸进行等比例缩放,叶型截面如图1所示,叶栅的主要几何参数及气动参数如表1所示. 压气机间隙高度通常不超过3%h,为了更为有效地观察来流马赫数的影响效果,本文选择流场变化程度最大的3%h作为叶顶间隙高度[12].Ma=0.7为亚声速和跨声速的分界值,文中马赫数选择Ma=0.5、0.6及0.7这3个数值. 为了完成后续实验过程中可以对叶片间隙高度进行调节的实验目的,实验过程中采用悬臂叶片变间隙的设计方案,原型叶栅和加装不同宽度压力面叶尖小翼的扩压叶栅都各有9片叶片,实验叶栅结构如图2所示.
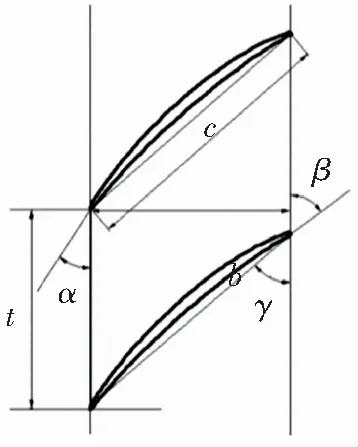
图1 实验叶栅叶型
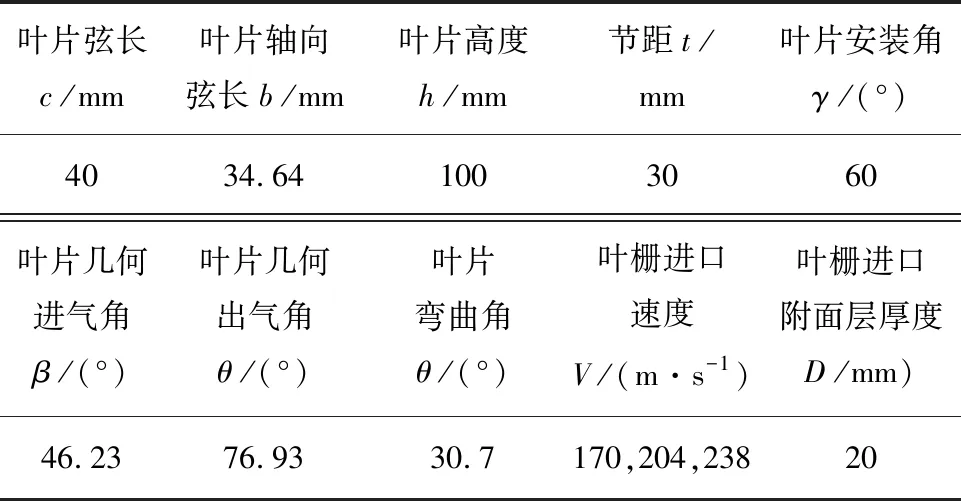
表1 主要几何参数

图2 叶栅实验段照片
叶尖小翼的上平面与原叶顶平面平行,无叶尖小翼命名为NW,压力面叶尖小翼宽度分别选取当地叶片宽度的1.0倍、1.5倍及2.0倍,分别命名为PW1.0、PW1.5及PW2.0,小翼结构如图3所示. 在高亚声速的来流条件下,叶尖小翼结构加装在叶顶时必然要承受高速旋转所带来的离心力的作用,在实验过程中小翼要承担较大的进口气流带来的作用力,为了防止小翼结构在实验过程中由于受力而脱落,研究过程中将小翼结构与叶片顶部采用光滑过渡的融合设计,采用融合式叶尖小翼方案可以有效保证实验过程的安全和准确性.

图3 不同形状叶尖小翼示意图
Fig.3 Schematic diagram of prototypes and different shapes of winglets
1.2 实验测点布置
在平面叶栅实验过程中叶顶结构的变化对流场区域的影响只集中于叶片上半叶高[7],为缩短实验周期、减少实验成本,研究过程只对叶片的上半叶高进行了测量. 为完整测量泄漏涡与上通道涡结构,近上端壁区域叶顶间隙区域布点加密,此外尾迹区域也加密,以保证在不同来流冲角下将主流区尾迹与角区高损失区全部覆盖. 加密方法为对最小冲角尾迹与最大冲角尾迹之间的区域全部进行加密,此种方法不需每次调整布点方案,减小了工作量,另一方面也规避了流场信息测量不全的风险. 在本方案中叶高方向分布了24个不等间距测量位置,节距方向分布了23个不等间距测量位置,共有测量点552个,布点方式如图4所示,图中横纵坐标已经分别进行了无量纲化. 叶栅上端壁静压测点分布如图5所示,共98个静压孔.
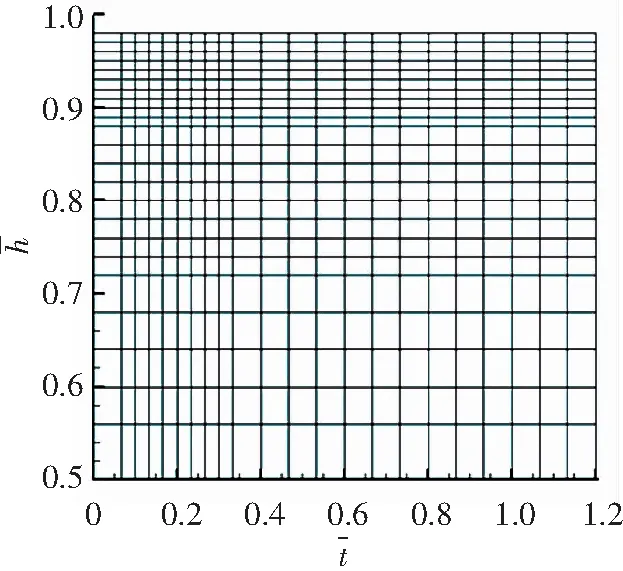
图4 出口测量截面布点图

图5 上端壁静压测点分布图
实验结果分析过程中的性能参数定义如下:
静压系数为
(1)
总压损失系数为
(2)
式中:Ps为绝对值静压,Psbi为叶栅上端壁各点静压,Pvb为栅前动压,Ptb为栅前总压,Pe为测量点总压. 现有研究证明叶片顶部的泄漏涡起始位置对应着上端壁壁面静压值最小点,静压斜槽的位置可以有效表征泄漏涡的运行轨迹[13-14]. 总压损失系数是用来衡量叶轮机械气动性能的主要参数,数值越小代表流动损失越小[15].
1.3 流场周期性
叶栅出口处的流场周期性是衡量气流均匀性的主要参数,图6为Ma=0.7时叶栅出口截面的总压损失系数沿节距方向分布图. 由图6可知出口截面的流场周期性较好,满足本次实验对出口流场均匀性的要求.
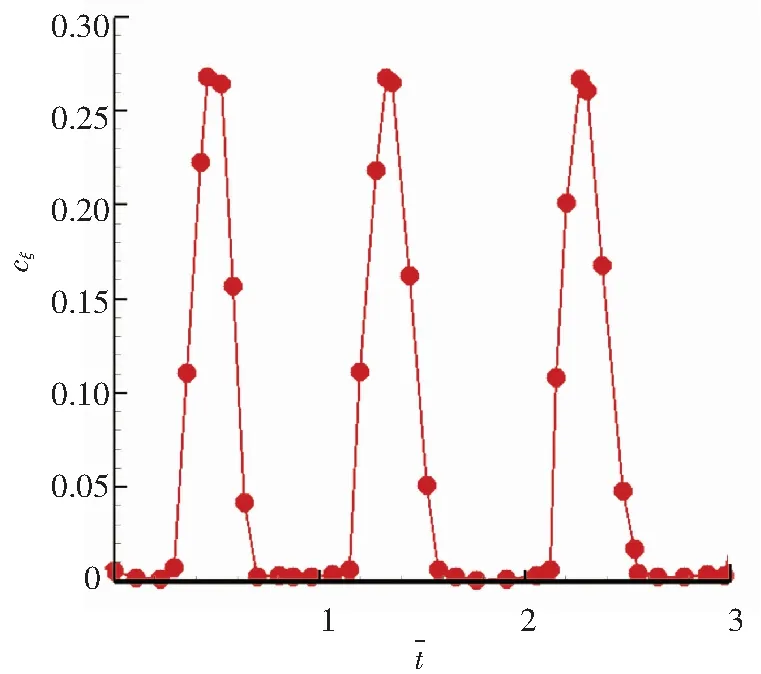
图6 叶栅出口流场周期性
1.4 误差分析
在进行实验的过程中,不可避免地会存在一定的误差,如实验设备等绝对误差是人工不可调解的,但其他相对误差可以尽量减小,如使用误差及环境误差等. 在完成进口、壁面及出口实验参数测量过程中主要测量仪器精度如表2所示.

表2 主要测量仪器精度
本文实验过程中所用的三孔探针及五孔探针的角度定位误差均小于1°,测量点的定位误差均小于0.5 mm,对总压及静压的测量不确定度小于1%. 仪器的精度满足本次实验要求,可以保证测量结果的精确性.
2 结果分析
2.1 叶顶区域流场
图7为不同马赫数下无叶尖小翼压气机叶栅和

图7 不同马赫数叶栅上端壁静压系数分布
不同宽度压力面叶尖小翼方案压气机叶栅的上端壁静压系数分布. 不同马赫数下都存在明显的静压斜槽,由低压区域存在位置可知此时流场中泄漏涡成为主要涡系,即流动损失增加的主要因素. 随着马赫数的增加,NW方案低压区域明显增大. 当Ma=0.5时,加装不同宽度的压力面叶尖小翼都可以延迟泄漏流动与主流的掺混,减少掺混损失,使泄漏涡强度减弱. 随着叶尖小翼宽度的增加,对流场的改善效果越明显,静压斜槽都向叶片吸力面有所迁移. 当Ma=0.6时,由于流体动能增加,泄漏涡产生的损失更大,NW方案流场中的低压区域变大,不同宽度的压力面叶尖小翼都会减小叶顶两侧的压力梯度,抑制泄漏流动的产生,降低流动损失,PW2.0方案仍然对NW流场效果改善最大. 当Ma=0.7时,NW方案中低压区域的增加程度明显大于Ma=0.6与Ma=0.5时的增加程度,这是由于Ma=0.7时,流场已经处于高亚声速的临界值,和其他低马赫数工况相比流场特性发生变化,泄漏涡的强度变化对流场的影响程度增加,泄漏涡成为流场中最主要的涡系,压力面叶尖小翼对其强度和空间位置的影响成为流场的中最为主要的变化因素. 不同宽度的叶尖小翼都使得泄漏涡强度减弱,起始位置有所后移,且随着叶尖小翼宽度的增加,改善效果更加明显.
2.2 流场内熵变化
熵是指体系的混乱程度,是一种较为准确的表征流动损失的气动参数,由于流动损失通常是由复杂的流动涡系相互作用产生的,因此高熵区域通常对应中高流动损失区域. 为了直观地观察叶栅流场的变化,在同样的来流条件下对不同工况的叶栅进行数值计算,数值计算方法的可靠性已在作者发表的文章中得到验证[12],从叶顶前缘为起点沿轴向截取了13个等距离截面,不同方案沿着流动方向的熵分布云图如图8所示.

图8 不同马赫数叶栅熵分布云图
当Ma=0.5时,不同宽度的压力面叶尖小翼减少了叶顶两侧的压力梯度,延迟了泄漏涡的起始位置,对压力面侧要进入叶顶间隙区域的流体有阻碍作用,降低了叶顶间隙泄漏流体的速度,泄漏涡强度降低,高熵区域减小,流场稳定性增加,且随着叶尖小翼宽度的增加,改善效果愈加明显.
当Ma=0.6时,不同方案的压气机叶栅中熵增均大于各方案对应的Ma=0.5工况,压力面叶尖小翼对于流场的改善效果基本一致. 随着叶尖小翼宽度的增加,叶尖小翼对于叶顶间隙泄漏流体的抑制能力加强,流场中熵增逐渐减弱,泄漏涡强度减弱,流动损失减小.
当Ma=0.7时,流场中流动特性与其他马赫数工况时相比有所变化,此时的流场处于向跨声速过渡的临界区域,流场中泄漏涡的影响范围明显增加,高熵区域在流动方向和节距方向都有明显增加. PW1.0方案时,泄漏涡起始位置后移,延迟了泄漏流与主流的掺混,泄漏涡受到明显抑制,流场中的高熵区域明显减小. PW1.5方案时,叶尖小翼对流场的改善效果更加明显,高熵区域进一步减小. 当PW2.0方案时,叶尖小翼进一步削弱了泄漏涡的强度,高熵区域再次减小,流动损失明显降低. 同时更多的附面层低能流体随着通道涡的发展而被卷吸离开端壁,沿着流动方向横向压力梯度增强,端壁间隙区横向流动增加,被削弱的泄漏涡无法将这部分补充流体卷吸形成旋涡结构,间隙区域横向流动加强,在靠近上端壁节距方向高熵区分布范围有所扩张.
2.3 出口截面流场
图9与图10分别给出了实验测得不同方案下的出口截面总压损失系数分布图及二次流分布图(对横坐标节距与纵坐标叶片高度进行无量纲化,出口截面距离前缘150%轴向弦长处). 图中分别标识出了各旋涡结构,其中叶顶泄漏涡(Tip Leakage Vortex)简称为TLV,上通道涡(Up Passage Vortex)简称为UPV,上集中脱落涡(Up Concentrated Shed Vortex)简称为UCSV. 漏流体在流出叶顶间隙区域后在主流的作用下卷吸成为与通道涡旋向相反的叶顶泄漏涡,上通道涡主要是由于马蹄涡在叶片压力面的分支受到上端壁横向压力梯度的作用不断卷吸上端壁附面层低能流体形成的,此时端壁附面层的低能流体会向叶片吸力面的角区进行移动与堆积,并与主流进行掺混. 泄漏涡与通道涡旋向相反,相互制约. 除此之外流场中还存在着上集中脱落涡,上集中脱落涡是由端壁与吸力面角区附面层的低能流体与尾缘脱落涡相互黏性剪切而产生的,上集中脱落涡与上通道涡旋向相反,两者的相互作用也造成了一定的流动损失. 此时流场中的总压损失主要是由叶顶泄漏涡、上集中脱落涡、上通道涡及三者互相的影响引起的.

图9 不同马赫数叶栅出口总压损失系数分布

图10 不同马赫数叶栅出口二次流分布
当Ma=0.5时,NW方案的出口截面主要存在泄漏涡、上通道涡及上集中脱落3种涡系. PW1.0方案时,小翼的出现削弱了叶顶两侧压力梯度,泄漏流动得到抑制,泄漏涡涡核对应的高损失区域面积减小,影响范围减小;上通道涡的节距与径向范围有所增大,上集中脱落涡分布范围明显增大,但两者的强度变化小于泄漏涡对流场的影响程度,因此此时泄漏涡的减弱使得流场总压损失降低. 随着叶尖小翼宽度的增加,泄漏涡涡核对应的高损失区域面积进一步减小,上集中脱落影响范围增大,流场的流动损失逐渐减小. 其中PW2.0的改善效果最为明显. 当Ma=0.6时,随着马赫数的增加,NW、PW1.0、PW1.5及PW2.0各方案出口截面上的总压损失都有所增加,叶尖小翼对于流场的改善规律与Ma=0.5时相同. 随着叶尖小翼宽度的增加,泄漏涡强度减弱,影响范围减小,上通道涡与上集中脱落涡强度增加,空间尺寸增大,流场的总压损失降低. 当Ma=0.7时,此时NW方案出口截面上泄漏涡成为最重要的涡系结构,分布于整个节距范围,上通道涡与上集中脱落涡被完全抑制. PW1.0方案时,泄漏涡强度明显减弱,涡核对应的高损失区域明显减小,其在节距的影响范围减小,上通道涡则在节距的尺寸增大,并出现上集中脱落涡. PW1.5方案时,泄漏涡进一步减弱,集中脱落涡有所增强. PW2.0方案时,叶尖小翼附加损失对流场的不利影响弱于其对流场中泄漏涡的强度的改善效果,此时泄漏涡强度进一步减弱,影响范围减小,上集中脱落涡面积明显增大,总压损失进一步降低.
2.4 性能参数
图11为不同马赫数下无叶尖小翼压气机叶栅与加装3个不同宽度压力面叶尖小翼叶栅出口截面的节距质量平均总压损失系数沿叶高的分布情况. 当Ma=0.5时,在80%h~90%h区域内,叶尖小翼所带来的附加摩擦损失随着小翼宽度的增加逐渐增大. 90%h~100%h区域,叶尖小翼宽度的增加使其对流场泄漏流动的抑制作用逐渐增强,此时PW2.0方案最大程度地降低了流场的总压损失. 当Ma=0.6时,叶尖小翼对流场的控制规律与Ma=0.5时相同,PW2.0方案对流场的改善程度最大,随着马赫数的增加,泄漏流量增加,泄漏流体动能增强. 泄漏涡对流场的影响更加剧烈,不同方案的叶尖小翼对流场的改善程度增加. 当Ma=0.7时,流场中泄漏涡在径向方向的影响范围增加,叶尖小翼对流场的影响更为明显,在80%h~100%h区域都可以体现叶尖小翼的改善作用,随着叶尖小翼宽度的增加,泄漏涡逐渐减弱,总压损失逐渐减小.
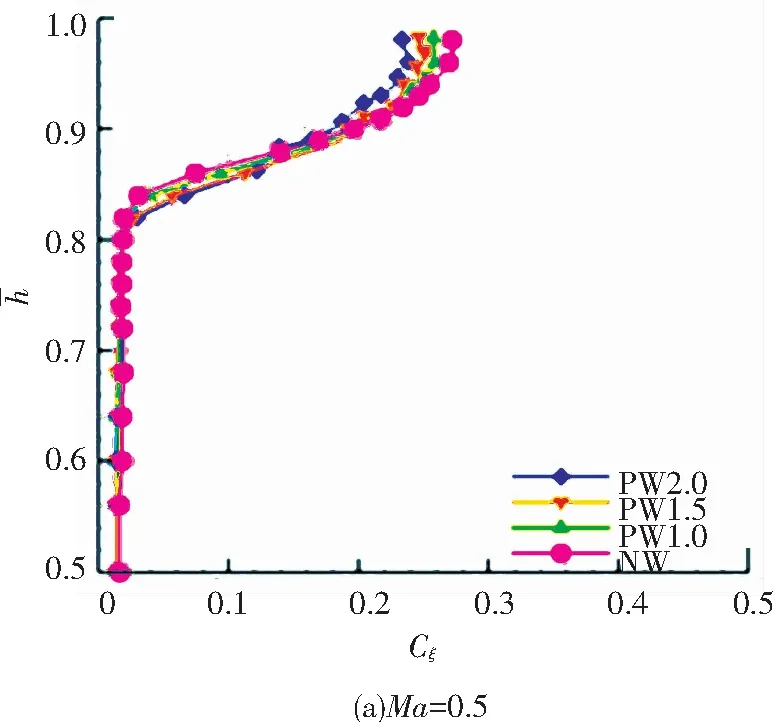


图11 节距平均出口总压损失系数沿叶高分布
Fig.11 Spanwise distribution of pitch-averaged total pressure loss coefficient
图12为不同方案压气机叶栅出口截面总压损失系数随马赫数变化的曲线图. 在不同的来流马赫数工况下,不同宽度的压力面叶尖小翼都降低了流场的总压损失,且叶尖小翼宽度与改善程度成正比. 随着马赫数的增加,压力面叶尖小翼对流场的改善程度增加. 当Ma=0.5时,PW2.0的总压损失与NW方案相比降低了4.06%. 当Ma=0.6时,与NW方案相比,PW2.0的总压损失降低了4.95%. 当Ma达到0.7时,PW2.0的改善效果更为明显,其总压损失降低了6.53%.
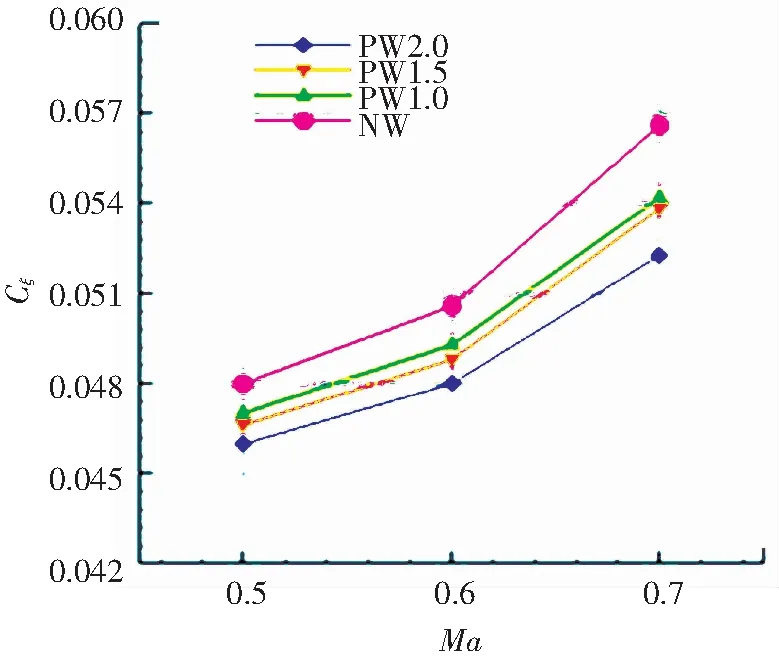
图12 出口质量平均总压损失系数
压气机的出口气流角可以直接反映气流在流动过程中的折转程度,并在一定程度上表征流场中附面层流动及二次流涡系的分布情况. 气流的折转程度越小,气流稳定性越高[7]. 图13为不同马赫数下无叶尖小翼压气机叶栅与加装3个不同宽度压力面叶尖小翼叶栅出口截面节距质量平均出口气流角沿叶高的分布. 由于泄漏涡的形成机理与流动特性,出口气流角会沿着叶高方向先后出现过偏转和欠偏转现象. 当Ma=0.5时,不同方案的压气机叶栅出口截面的气流角沿叶高出现过/欠偏转现象. 随着叶尖小翼宽度的增加,泄漏流动得到抑制,泄漏涡强度减弱,作用范围减小,出口气流角沿叶高过/欠偏转现象逐渐减弱,气流均匀性增强. 随着马赫数的增加,叶尖小翼对出口均匀性的改善机理相同,即当Ma=0.6和Ma=0.7工况时,叶尖小翼宽度的增加和对出口流场的控制效果成正比,PW2.0方案都是其工况下的最佳工况. 同时马赫数增加使得泄漏流动加强,可以观察到叶尖小翼的改善程度逐渐增加.

图13 节距平均出口气流角沿叶高分布
3 结 论
1)在高亚声速来流条件时,不同来流马赫数下,不同宽度的压力面叶尖小翼都降低了流场的流动损失,增加了出口气流的均匀性,压力面叶尖小翼区域的低能流体不但减弱了叶片两侧的压力梯度,还会对进入叶顶间隙区域的流体起到阻碍作用.
2)随着压力面叶尖小翼宽度的增加,泄漏流动需要流经的路程增加,进入叶顶间隙的流体减少,泄漏流动能量减弱,泄漏涡强度减弱,泄漏流动的控制效果与叶尖小翼宽度成正比.
3)随着马赫数的增加,流场中泄漏流动逐渐增强,压力面叶尖小翼的改善效果逐渐增强. 当Ma=0.5时,PW2.0的总压损失与NW方案相比降低了4.06%. 当Ma=0.6时,与NW方案相比,PW2.0的总压损失降低了4.95%. 当Ma达到0.7时,PW2.0的改善效果更为明显,其总压损失降低了6.53%.
4)加装压力面叶尖小翼后,与同工况的原型叶栅相比,流场的变马赫数敏感性有效降低,变工况下高亚声速压气机叶栅流场更为稳定,气流更为均匀,流动状况得到明显改善,高亚声速的来流条件下压力面叶尖小翼是一种有效的泄漏流动控制手段.

