路的强积的邻点可区别边染色

安卓莫 ,田双亮,2,蔡 瑾

(1.西北民族大学 数学与计算机科学学院,甘肃 兰州 730030；2.西北民族大学 动态流数据计算与应用重点实验室,甘肃 兰州 730030)

0 引言

本文所考虑的图G都是有限、无向的简单连通图,用V(G)与E(G)分别表示G的顶点集和边集,并用Δ(G)表示G的最大度，记(x)k=x(modk),其中x为整数,k为正整数.

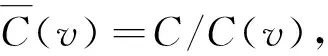
由邻点可区别边染色概念,容易得到以下引理.

引理1.1 若阶至少为3的简单图G中存在相邻的最大度点,则

χ＇α(G)≥Δ(G)+1.

zhang等在文献[1]中提出了邻点可区别边染色概念,并研究了一些基本简单图，如路、圈、完全图、树等的邻点可区别边染色,得到了相应的邻点可区别边色数.Balister在文献[2]中证明了最大度为3的图的邻点可区别边色数不超过5,二部图的邻点可区别边色数不超过其最大度加2,并证明这些上界是可达的.Hatami在文献[3]中证明了任意图的邻点可区别边色数不超过其最大度加300.由于图的结构运算是构造图的重要方法和手段,因此,研究运算图的邻点可区别的边染色有助于确定一般图类的相应染色数.常见的图结构运算有图的字典积、图的笛卡尔积、图的联，以及图的半强积、直积等等.Tian等在文献[4]与[5]中研究了一些特殊图的字典积与笛卡尔积的邻点可区别的边染色,得到了相应的邻点可区别边色数.Baril、Chen等在文献[6]与[7]中得到了一些网格图与超立方体的邻点可区别的边色数.何雪等在文献[8]中给出了一些特殊图的倍图(即二阶路与图的半强积)的邻点可区别边色数.

设Pm=v0v1…vm-1,Pn=v0v1…vn-1是两条路,其中m,n≥2.为了方便叙述,用(x,y)表示V(Pm)×V(Pn)中的顶点(uy,ux).文中未说明的符号及术语可参考文献[10].

1 路的强积的邻点可区别边染色

σ((x,y)(x,(y+1)2))=(x+2)6,x=0,1,…,n-1,y=0，1，

σ((x,y)(x+1,(y+1)2))=(x+4)6,x=0,1,…,n-2,y=0，1，

σ((x,y)(x+1,y))=(x+y)6,x=0,1,…,n-2,y=0，1.

显然,σ所用颜色集合为C={0,1,…，5}.

首先,验证σ是G的正常边染色.对每一个顶点(x,y)∈V(G),当1≤x≤n-2时,顶点(x,y)的关联边分别为

e1=(x,y)(x+1,y),e2=(x,y)(x+1,(y+1)2),e3=(x,y)(x,(y+1)2),

e4=(x-1,(y+1)2)(x,y),e5=(x-1,y)(x,y).

当x=0时,顶点(x,y)的关联边分别为

e1=(x,y)(x+1,y),e2=(x,y)(x+1,(y+1)2),e3=(x,y)(x,(y+1)2).

当x=n-1时,顶点(x,y)的关联边分別为

e3=(x,y)(x,(y+1)2)(x,y),e4=(x-1,(y+1)2)(x,y),e5=(x-1,y)(x,y).

由σ定义可知,5条边e1、e2、e3、e4、e5的颜色分别为

σ(e1)=(x+y)6,σ(e2)=(x+4)6,σ(e3)=(x+2)6,

σ(e4)=(x+3)6,σ(e5)=(x+y-1)6=(x+y+5)6

容易验证,这5条边染不同的颜色,即σ是G的一个正常边染色,且有

C(0,y)={y,2,4},C(n-1,y)={(n+1)6,(n+2)6,(n+y+4)6},y=0,1.

(1)

(2)

其次,验证σ是邻点可区别的.显然,仅需证明具有相同度的相邻顶点有不同的色集.任取度相同的两个相邻顶点u=(x,y)与u=(x＇,y＇),不妨设x≤x＇.假设C(u)=C(v),则可推出矛盾.

根据路的强积的结构特征,d(u)=3或d(u)=5,且v可能是3个顶点之一：

①v1=(x+1,y);②v2=(x+1,(y+1)2);③v3=(x,(y+1)2).

若d(u)=3,则v=v3=(x,(y+1)2).此时,x=0或x=n-1.当x=0时,由式(1)可知,对每一y=0,1,有C(u)={y,2,4},C(v)={(y+1)2,2,4}.

当x=n-1时,对每一y=0,1,有

C(u)={(n+1)6,(n+2)6,(n+y+4)6},C(v)={(n+1)6,(n+2)6,(n+(y+1)2+4)6}.

由C(u)=C(v)可推出矛盾:y=(y+1)2.

又因C(u)=C(v),所以(4((y)2-(y+1)2))6=1,这是不可能的,因(y)2-(y+1)2=±1.当v=v3时,则1≤x≤n-2,由式(2)可知,

由C(u)=C(v)可推出矛盾：(y)2=(y+1)2.

由以上分析,σ是邻点可区别的.因此,定理结论成立.

σ((x,y)(x+1,y))=(x+2y)9,x=0,1,…，n-2,y=0,1,…，m-1；

σ((x,y)(x,y+1))=(x+2y+4)9,x=0,1,…，n-1,y=0,1,…，m-2；

σ((x,y)(x+1,y+1))=(x+2y+1)9,x=0,1,…，n-2,y=0,1,…，m-2；

σ((x,y+1)(x+1,y))=(x+2y+7)9,x=0,1,…，n-2,y=0,1,…，m-2.

显然,σ所用颜色集合为C={0,1,…，8}.

首先,验证σ是G的正常边染色,对每个顶点(x,y)∈V(G),顶点(x,y)的所有可能关联边分别为

e1=(x,y)(x+1,y),e2=(x,y)(x+1,y+1),e3=(x,y)(x,y+1),e4=(x-1,y+1)(x,y),

e5=(x-1,y)(x,y),e6=(x-1,y-1)(x,y),e7=(x,y-1)(x,y),e8=(x,y)(x+1,y-1).

由σ定义可知,边e1,e2,…，e8所染颜色分别为

σ(e1)=(x+2y)9,σ(e2)=(x+2y+1)9,σ(e3)=(x+2y+4)9,σ(e4)=(x+2y+6)9

σ(e5)=(x+2y+8)9,σ(e6)=(x+2y+7)9,σ(e7)=(x+2y+2)9,σ(e8)=(x+2y+5)9.

容易验证,(x,y)的不同关联边染不同颜色,即σ是G的一个正常边染色,且对x=1,2,…，n-2,y=1,2,…，m-2,有

(3)

(4)

(5)

(6)

(7)

其次,验证σ是邻点可区别的.显然,仅需证明具有相同度的相邻顶点有不同的色集.任取度相同的两个相邻顶点u=(x,y)与v=(x＇,y＇),不妨设x＇≥x,且当x＇=x时,设y＇>y,假设C(u)=C(v),可推出矛盾.

由路的强积的结构可知,d(u)=5或d(u)=8.下面分两种情况讨论.

情况1d(u)=5.此时,u的邻点v是以下两种情况之一：①v=(x,y+1),其中x=0或x=n-1,y=1,2,…，m-3；②v=(x+1,y),其中y=0或y=m-1,x=1,2,…，n-3.

①v=(x,y+1).当x=0时,由式(3)可知,对y=1,2,…，m-3,顶点u与v上缺少颜色之和,分别为

②u=(x+1,y).当y=0时,由式(5)可知,对x=1,2,…，n-3,顶点u与v上缺少颜色之和,分别为

情况2d(u)=8.此时,u的邻点v是以下四种情况之一：

①v=v1=(x+1,y)，其中x=1,2,…，n-3,y=1,2,…，m-2;

②v=v2=(x,y+1),其中x=1,2,…，n-2,y=1,2,…，m-3;

③v=v3=(x+1,y+1),其中x=1,2,…，n-3,y=1,2,…，m-3;

④v=v4=(x+1,y-1),其中x=1,2,…，n-3,y=1,2,…，m-2.

由式(7)可知,顶点u及其邻点的缺少颜色集合分别为

显然,对每一i=1,2,3,4,有C(u)≠C(vi),这与C(u)=C(v)矛盾.

综合情况1与情况2，σ是邻点可区别的.因此,定理结论成立.