发射筒水循环空调热负荷仿真计算方法
王向往,刘 东,张 剑,党帅营,郭敬彬
(1.中国船舶集团公司第七一三研究所,河南 郑州 450015;2.河南省水下智能装备重点实验室,河南 郑州 450015)
0 引 言
在潜载导弹发射装置中,空调系统承担着调节发射装置筒内温度,为导弹提供合适贮存条件的重要功能,是发射装置的重要组成部分。空调系统一般分为通气空调和水循环空调,其中水循环空调是利用管路中水温的高低对发射筒内实现供热或供冷的效果,从而保证发射筒内温度的恒定[1–2]。
水循环空调管路布置在发射装置发射筒内壁,基于空间有限,需要首先计算出发射筒的空调热负荷,求出所需水管的管道表面积,进而验证发射筒内壁面空间能否满足水循环空调方案的需求。一般采用稳态的方法计算空调的热冷负荷,根据能量守恒定律,空调热负荷即通过发射筒壁面散失或者吸收的热量[3]。发射筒在夏季吸收热量最多,在冬季散失热量最多,所以只需要计算出发射筒在夏、冬两季的空调热负荷,即可知道空调的极限热负荷。
1 仿真模型
1.1 物理模型
潜载导弹发射装置发射筒的主要组成包括内筒、外筒、筒底、筒盖。
发射筒实际结构非常复杂,整体进行建模计算量很大。本文通过简化发射筒模型计算空调热负荷,为了简化分析需做以下基本假设:
1)认为各层材料物性均匀不变,并且忽略层与层之间的接触热阻;
2)由于发射筒温度分布具有对称性,在取局部模型进行传热计算时,可设温度分布对称处为绝热;
3)发射筒筒状结构轴向方向温度不变;
简化模型相关计算可以为实际的空调热负荷提供参考。简化模型如图1 所示。

图1 发射筒几何结构示意图Fig.1 Geometry diagram of launcher
发射筒上部暴露于空气的时候空调热负荷最大,这时发射筒从所面对的外部环境角度分析,可以分为舷外段、舱内段和筒底段3 个部分。其中舷外段外部环境为空气,舱内段外部环境为舱室环境,筒底段外部环境为海水。
考虑到舱内段发射筒外部环境是舱室,本身已有空调调节温度,可以忽略舱内段发射筒的内外温差,即不用考虑舱内段的空调热负荷,仅考虑舷外段和筒底段。简化后的模型轴向方向相同部位所处环境一样,传热过程和材料结构一样。所以通过局部仿真计算得到平均热流密度,再与换热面积相乘得到每段换热量,最后相加可得到总的发射装置热负荷。发射筒外筒内外壁面考虑一定厚度保温层,内外筒之间有一定间隙,赋予空气的属性;筒盖内外壁面考虑有一定厚度保温涂层;筒底内侧考虑有保温涂层,外侧考虑有一定厚度的绝缘材料。舷外段筒盖和圆筒局部模型如图2 和图3 所示,筒底段模型如图4 所示。

图2 筒盖局部模型示意图Fig.2 Schematic diagram of local model of cylinder cover
简化模型中筒盖,圆筒段,底部的内表面面积分别记为 A1, A2, A3。
1.2 仿真理论及计算公式
发射筒通过壁面的换热过程有热传导和对流传热2 种。热传导相关计算公式如下:

其中: q为热流密度, W /m2; k 为 导热系数, W /(m·k);为传热方向上的温度梯度。对流换热相关公式如下:

图3 圆筒局部模型示意图Fig.3 Schematic diagram of local cylinder model

图4 筒底模型示意图Fig.4 Schematic diagram of cylinder bottom model

其中: q 为热流密度, W /m2; h 为对流换热系数,W/(m2·k) ; TS为物体表面温度, T∞为流体温度,K。热流密度与换热量相关公式如下[4]:

其中: q 为热流密度, W /m2; A为模型的内表面面积, m2, Q 为换热量, W。发射筒内温度由管路控制,管路与发射筒内热量交换有辐射与对流2 种,其中辐射占主要部分[5]。本文的计算忽略对流,按照ASHRAE 计算方法提供的辐射供冷方程计算管路与发射筒内的热交换效率[6–7],方程如下:

其中: Qr为 单位面积辐射换热量,W/m2; tp为有效辐射板的表面温度,℃;AUST 为除辐射板以外空间表面加权平均温度,℃。根据能量守恒定律,发射筒通过壁面散失或吸收的热量与管路向发射筒内传递或者吸收的热量相等,则所需管路表面积为:

首选通过仿真计算得到热流密度,代入式(3),可得到夏季和冬季的空调热负荷。选取管路温度 tp,代入式(4)和式(5),可得到选取的管路温度对用的管路表面积。
1.3 材料参数
仿真计算中相关材料的导热系数可以通过资料直接查询得到,取值如表1 所示。不同部位对流换热系数取值如表2 所示[8–10]。其中内外筒、筒盖、筒底材料选取碳钢来进行计算。

表1 相关材料热学性能参数Tab.1 Thermal performance parameters of related materials

表2 不同部位对流换热系数Tab.2 Convective heat transfer coefficient of different parts
1.4 网格划分及边界条件
使用Ansys 软件对三维模型进行网格划分。筒盖局部模型不规则,网格类型采用四面体网格,网格数28195 个,如图5 所示。计算时保温涂层与筒盖之间采用绑定约束,把发射筒内环境温度赋予筒盖内侧保温涂层表面,赋予筒盖外侧保温涂层与环境之间对流换热条件,对流换热系数如表3 所示,环境温度即外部空气温度。其他面赋予绝热条件。

图5 筒盖局部模型网格示意图Fig.5 Grid diagram of local model of cylinder cover
圆筒段模型是一个规则的圆筒形状,采用的网格类型为六面体网格,网格数14152 个,如图6 所示。内外筒间空气赋予流体性质,计算时保温涂层与筒盖之间采用绑定约束;外筒内外保温涂层表面与空气之间赋予对流换热条件,内筒外壁与筒间空气赋予对流换热条件,对流换热系数取表3 中值。根据所处环境给予内筒内壁温度与发射筒内温度一致,外筒外壁保温涂层外部环境温度与环境空气温度一致。其他面给与绝热条件。

图6 圆筒段局部模型网格示意图Fig.6 Grid diagram of local model of cylinder section
筒底段模型是一个带弧度的圆板,采用的网格类型为六面体网格,网格数26536 个,如图7 所示。计算时保温涂层与筒盖、保温层与筒底之间采用绑定约束,保温涂层表面赋予发射筒内部环境温度,底部是海水环境,直接给表面赋予与海水温度。其他面赋予绝热条件。

图7 筒底模型网格示意图Fig.7 Grid diagram of cylinder bottom model
2 夏季工况分析
2.1 夏季舷外段传热过程
舷外段传热过程分为圆筒段传热过程、筒盖传热过程。夏季发射筒内部温度比外部环境温度低,是一个吸热的过程。用Ansys Workbench 18.0 模拟传热过程,得到舷外段夏季筒盖内壁平均热流密度 q1及圆筒段内壁平均热流密度 q2。局部热流密度计算结果云图如图8 和图9 所示。
2.2 夏季筒底段传热过程

图8 夏季筒盖局部模型热流密度云图Fig.8 Heat flux nephogram of local model of cylinder cover in summer

图9 夏季圆筒段局部模型热流密度云图Fig.9 Local model heat flux nephogram of cylinder section in summer
筒底段内壁敷设保温层,外部有厚度一定厚度的材料绝缘。添加边界条件,得到夏季筒底段平均热流密度 q3,热流密度云图如图10 所示。

图10 夏季筒底段热流密度云图Fig.10 Cloud chart of heat flux density at the bottom of cylinder in summer
2.3 夏季管路表面积计算
夏季空调热负荷为:

假设夏季管路温度 tp1,发射筒内部温度AUST,代入式(4)和式(5),可得管路表面积为:
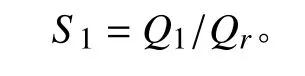
3 冬季工况分析
3.1 冬季舷外段传热过程
冬季发射筒内部温度比外部环境温度高,是一个散热的过程。修改边界条件,冬季舷外段局部热流密度计算结果云图如图11 和图12 所示。可得到冬季舷外段筒盖内壁平均热流密度 q4及 圆筒段内壁平均热流密度 q5。

图11 冬季筒盖局部模型热流密度云图Fig.11 Heat flux nephogram of local model of cylinder cover in winter

图12 冬季圆筒段局部模型热流密度云图Fig.12 Local model heat flux nephogram of cylinder section in winter
3.2 冬季筒底段传热过程
添加冬季筒底段边界条件,计算得到热流密度云图如图13 所示。可得到冬季筒底段内壁平均热流密度 q6。

图13 冬季筒底段热流密度云图Fig.13 Cloud chart of heat flux density at the bottom of cylinder in winter
3.3 冬季管路表面积计算
冬季空调热负荷为:

假设夏季管路温度 tp2,发射筒内部温度AUST,代入式(4)和式(5),可得管路表面积为:
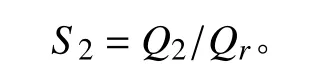
4 结 语
本文提出一种发射筒内水循环空调热负荷及管路表面积的计算方法。通过简化发射筒模型,对发射筒实际传热过程中环境条件与仿真计算时边界条件的转换进行描述。使用有限元仿真方法计算夏季和冬季情况下发射筒内部环境处于恒温时在所需的空调热负荷。最后用文中给出的方法,计算得到发射筒内采用水循环式空调所需的管路表面积。结果表明,这种方法是可行的。研究结果为发射筒空调热负荷计算提供一种方法,并且为发射筒内部水循环空调设计提供参考。

