混合数据信度优化模型及其在农作物保险定价中的应用
——以河北省县级玉米保险费率厘定为例
吴海平,李士森,李晓涛,任金政
(1.河北经贸大学 财政税务学院,河北 石家庄050061;2.石家庄铁路职业技术学院,河北 石家庄050061;3.中国农业大学,北京100083)
一、引言
农业保险是国家农业发展政策的重要组成部分,在保障粮食安全的同时也在粮食价格形成、农村金融制度创新、农业供给侧结构性改革等农业发展改革中扮演重要角色,已成为国家进行宏观调控的配套措施和重要抓手。自2007 年中央财政农业保险保费补贴政策实施以来,我国农业保险得到快速发展,截至2019 年,农业保险保费收入达到680 亿元,为全国1.8 亿户次农户提供了3.6 万亿元的风险保障,三大粮食作物覆盖率超过70%,为转移和分散我国农业风险发挥了重要作用。
费率如何厘定是农业保险可持续和高质量发展的关键问题,费率偏高会造成农户的有效需求不足,费率偏低又会增加保险机构的经营风险,无法提供长期的有效供给,并且精准的费率厘定也是国家进行风险区划、制定保费补贴政策、提高补贴资金使用效率的前提。精准的费率厘定需要以大量的经验数据为基础,由于农作物一般需要一年的生产周期,且生产过程和结果具有不可重现的特征,因此与其他财产保险相比,农业保险存在较为明显的经验数据不足的问题(张译元和孟生旺,2020)[1],并且相对于美国、印度等国家,我国在区域产量数据的收集方面存在劣势(黄正军,2016)[2],可公开获取的农作物生产和灾害数据时序较短,越小区域的数据获取越困难,给农作物灾害性损失的统计建模带来很大挑战,造成估计结果存在较大偏差和不稳定性,致使研究人员常常对结果的选择感到困惑,缺乏足够的可信度(肖宇谷等,2014)[3]。
为了更好地解决经验数据不足问题,本文建立了农业保险费率估计的信度优化模型,通过“借力”其他地区同分布数据横向扩大样本量,在此基础上提高我国农作物保险费率厘定的信度,以期为我国农业保险的精准化和专业化发展提供方法借鉴。
二、文献综述
现有文献厘定农作物保险费率的方法主要包括两类:经验费率法和统计模型法(李艳和陈盛伟,2018)[4]。从国外发达国家的实践来看,在历史损失数据样本连续、完整并充足的情况下,采用经验费率法,通过计算历史损失率的平均值能够得到具有较高精度和稳健性的费率(Goodwin and Piggott,2009)[5]。在历史保险损失数据不理想的情况下,学者一般通过统计建模对农作物单产损失的数据特征进行拟合,从而厘定农作物保险的费率(叶涛等,2012)[6]。统计模型法根据估计方法的不同可以分为参数法和非参数法(或半参数法),两种方法在国内文献中有大量应用,成为目前我国农作物保险费率厘定的主流方法,已形成较为成熟的研究模式。王 克(2008)[7]、叶 涛 等(2012)[6]、李 艳 和 陈 盛 伟(2018)[4]以及李政(2018)[8]等文献对费率厘定的统计模型方法做了较详细的综述。
但是,统计模型方法在厘定我国农作物保险费率时仍存在一定的不足,费率对产量分布的拟合方法非常敏感,无论是选择参数方法还是非参数方法,估计的费率都存在较大差异(肖宇谷等,2014)[3]。例如,参数法一般要预先假定样本数据服从一种或几种经典理论分布,然后利用分布拟合检验法(K-S检验、AD 检验或卡方检验)选择拟合程度最好的分布,预先设定分布本身就存在一定的不合理性,当样本量较小时,还经常出现拟合程度不高或接受多种不同分布类型的情况。再例如,非参数方法中较为常用的核密度函数法,虽然不必预先假设分布模型,但不同核函数,尤其是不同窗宽的选择会对估计结果造成较大影响(王克,2008)[7],并且非参数分布的估计方法需要较大的样本(Ker 和Goodwin,2000)[9]。吴垠豪(2014)[10]将新疆阿克苏市62 年的棉花产量数据作为“总体”,从中随机抽取14 年的数据作为“小样本”,利用参数法与非参数法估计费率,结果发现非参数法的估计结果与“总体”的差异更大,即在“小样本”情况下不宜采用非参数法估计农作物保险的费率。
综上而言,经验费率法、参数和非参数统计模型法的估计效果都受样本量的影响。相对于大样本而言,由于小样本数据遍历的观测较少,所蕴含的能够反映其总体分布特征的信息量低,因此在分布拟合时存在更多不确定性,基于此而得到的统计推断结果的可信度必然较低(郭建平等,2018)[11]。因此,当样本量较小时,各种方法估计得到的农作物保险费率的精准度和稳定性都较差。为增加农作物单产数据的样本量,部分学者提出了一些改进方法。例如肖宇谷等(2014)[3]利用Bootstrap 法对黑龙江省14 个区县的玉米保险费率厘定进行了分析,李文芳等(2009)[12]通过建立分层贝叶斯模型,利用Gibbs抽样对湖北荆州市县级水稻保险费率的厘定进行了研究。这些方法主要利用随机抽样技术增加可利用的样本量,但是抽样统计结果的好坏主要取决于初始样本量,样本量越大,抽样结果越接近真值。因此增加可利用的初始样本量是提高农作物保险费率厘定信度水平的根本。我国地域辽阔,当两个区域农作物的风险损失情况相近时,可将两个区域的数据混合到一起进行费率厘定,这样就增加了初始样本量。
本文基于保险费率厘定的信度理论,以提高费率估计的条件信度水平为出发点,通过构建和求解农业保险费率估计的信度优化模型,择优选择数据服从相同分布的区域,利用数据混合的方法扩大样本量,以增加我国农作物保险费率厘定的精确性和稳定性,并以河北省县域玉米保险费率的厘定为例验证了该方法的可行性和优势。
三、方法设计
不考虑保险机构经营成本和利润的情况下,公平的纯保险费用应等于期望损失,纯费率为期望损失与保障额度之比,即纯费率其中为期望达到的单产(保障水平),E(L(X))为期望损失。在保障水平一定的情况下,农作物保险费率厘定的核心步骤即为估计农作物灾害损失的期望。
假设某区域S0的灾害损失额X1,X2,…,Xn独立同分布,其期望值记为μ,该值即为风险保费,因此农业保险保费厘定的关键就是如何确定更为精确的μ 值。由于灾害损失的总体分布未知,一般利用平均损失额-X 作为μ 的近似估计值,其中=(X1+X2+…+Xn)/n。在保险理论中,若直接将平均损失额-X作为保费,则称作经验数据的完全信度,即保费厘定完全依靠现有的灾害损失数据。在完全信度下真实保费μ与之间的关系可以用式(1)表示。
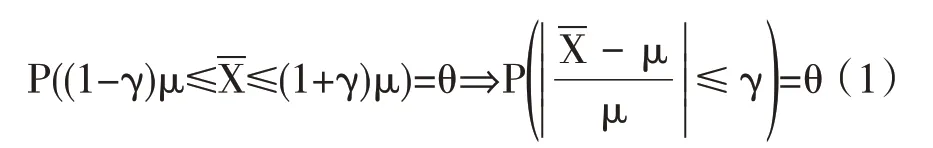
式(1)表示-X 与μ 之间的相对偏差不超过γ 的概率等于θ,即置信水平为θ。不等式两边同时乘以并除以标准差σ,式(1)变形为式(2),其中λ=
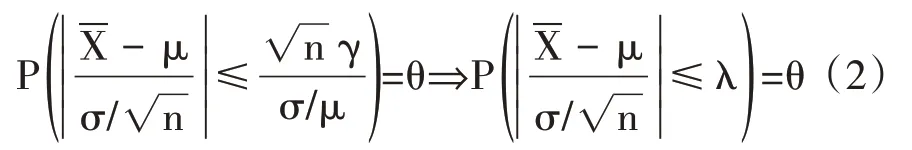

其中θh表示混合样本数据估计的信度水平,P(B)为区域S1,S2,…,SJ与区域S0同分布的概率,P(A|B)为同分布条件下混合数据估计的信度水平。事件B可以表示为B=B1⋂B2⋂…⋂BJ,Bj表示区域Sj与S0的样本数据具有相同的分布,由于Bi与Bj在i≠j时相互独立(区域Si和S0是否同分布与Sj和S0是否同分布为独立事件),根据独立事件概率公式有P(B)=P(B1)P因此式(4)可以转化为式(5)。
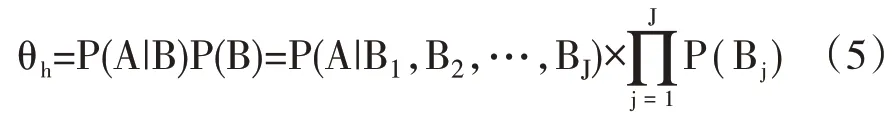
在同分布检验中,原假设(H0:区域Sj与S0的样本数据具有相同的分布)成立的概率为假设检验的p 值,由于原假设H0=Bj,因此P(Bj)=pj。由于K-S 检验对两样本经验分布函数的位置和形状参数的差异都比较敏感,是判断两样本(尤其是小样本情况)是否同分布的常用方法,因此可以利用K-S 检验计算同分布检验的p 值(K-S 检验的基本原理在此不再赘述)。
式(5)中θh由两部分构成,其中P(A|B1,B2,…,BJ)是混合区域个数和样本量的增函数,由于两个区域样本数据同分布的概率是混合区域个数的减函数。在样本量较小时,仅利用区域S0的数据估计的费率信度水平较低,而一般情况下能在置信水平较大的情况下找到同分布的其他区域进行数据混合,即P(Bj)较大,因此混合数据估计的信度水平θh会呈现倒U 形的变化特征,存在最优的混合区域,使得信度水平达到最大值θ*h,如图1 所示。
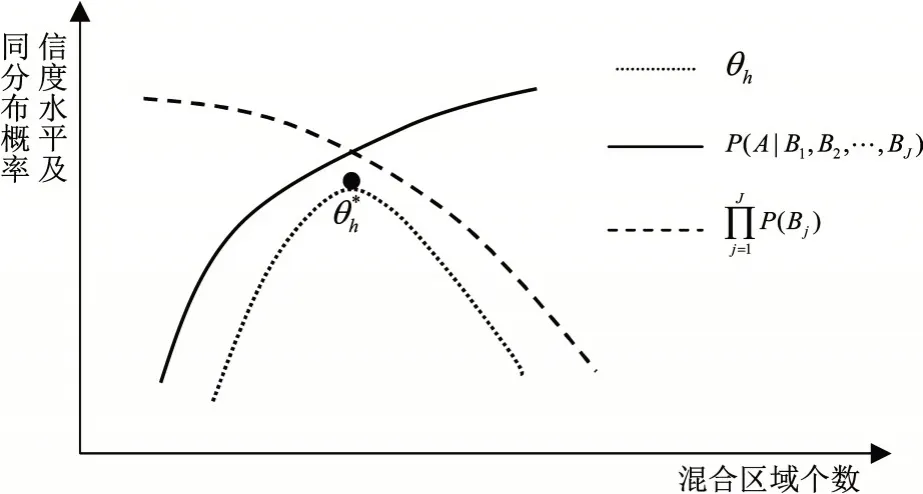
图1 混合数据信度水平与混合区域个数关系示意图
综上,通过如下方法和步骤可以利用混合数据方法增加样本量,提高农作物保险厘定费率的信度水平。一是将各区域的单产数据进行去趋势等相关处理;二是将各区域的样本数据进行两两K-S 同分布检验,获得假设检验的p 值;三是通过规划模型[式(6)]计算得到最优的区域进行数据混合和最大的信度水平θ*h;四是利用混合数据估计考察区域的保险费率。
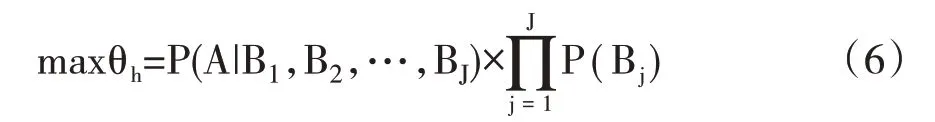
四、实证分析
玉米是重要的粮食作物和饲料作物,同时又是工业加工的重要原料,对国民经济发展具有重要影响。河北省是我国13 个玉米主产省之一,玉米生产在全国占有举足轻重的地位。本文以河北省玉米保险为例,基于1994—2017 年河北省县级玉米产量数据,利用上述方法厘定保险费率,验证上述方法的可行性,并为河北省玉米保险的开展提供参考。数据来源于1995—2018年的《河北省农村统计年鉴》。
(一)数据处理
2017 年年底河北省共有168 个县级行政区划(包含47 个市辖区、20 个县级市、95 个县、6 个自治县),其中27 个市辖区以及张家口市张北县、康保县、沽源县的数据缺失严重,在实证研究中剔除这30 个区域,因此本文最终基于138个县级区域1994—2017年的玉米单产数据进行研究。
2017 年河北省玉米总播种面积3544.06 千公顷(占全国玉米总种植面积的8.36%),总产量2035.48万吨(占全国玉米总产量的7.86%),平均亩产382.89公斤(是全国平均亩产的93.99%)。受玉米生产技术进步等因素的影响,玉米单产存在一定的增长趋势,因此需要通过趋势拟合计算得到单产的RSV 序列。农作物单产趋势拟合有多种方法,主要包括直线移动平均法(张峭等,2015)[13]、HP 滤波法(鄢姣和赵军,2014)[14]、回归分析法(肖宇谷等,2014)[3]以及时间序列预测方法,如灰色模型(Chen et al.,2015)[15]、ARMA 模型(Goodwin and Ker,1998)[16]等,各种方法具有不同的优势和缺点。本文采用非参数局部线性加权法估计河北省县级玉米单产趋势,该方法能够较好地克服其他模型中存在的模型设定或参数选择问题,能够更好估计农作物灾害性损失风险(任金政和李士森,2017)[17]。
本文以河北省省级玉米单产为例进行趋势拟合,趋势拟合结果如图2 所示。按照该方法利用MATLAB 软件估计河北省138 个县级区域的玉米单产趋势。
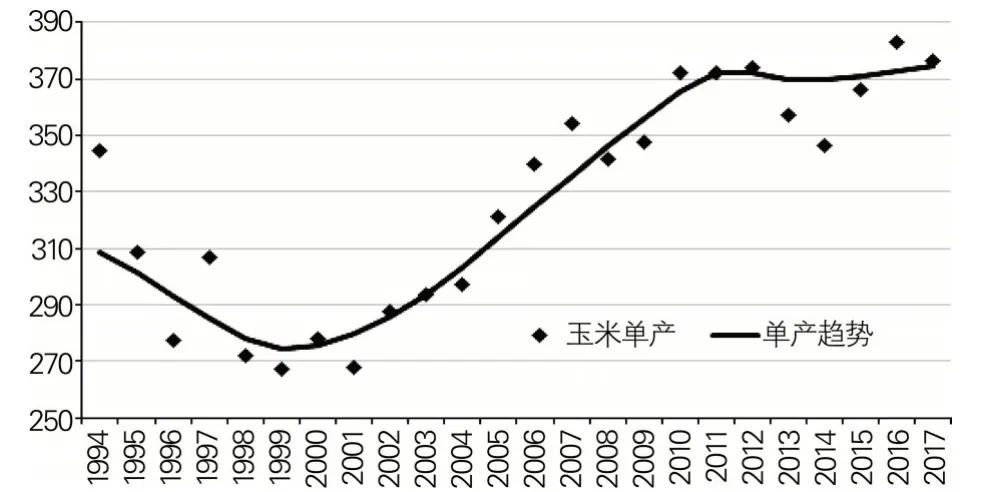
图2 河北省省级玉米单产及趋势拟合
根据趋势估计结果,可以将单产分解为Xt=X̂t+et,其中为玉米单产的趋势,et为估计残差。由于存在增长趋势,残差不具有可比性,因此需将估计残差转化为波动率xt=et/。利用MATLAB 软件计算得到河北省138 个县级区域玉米单产的波动率(RSV)序列,其均值变化情况如图3所示。
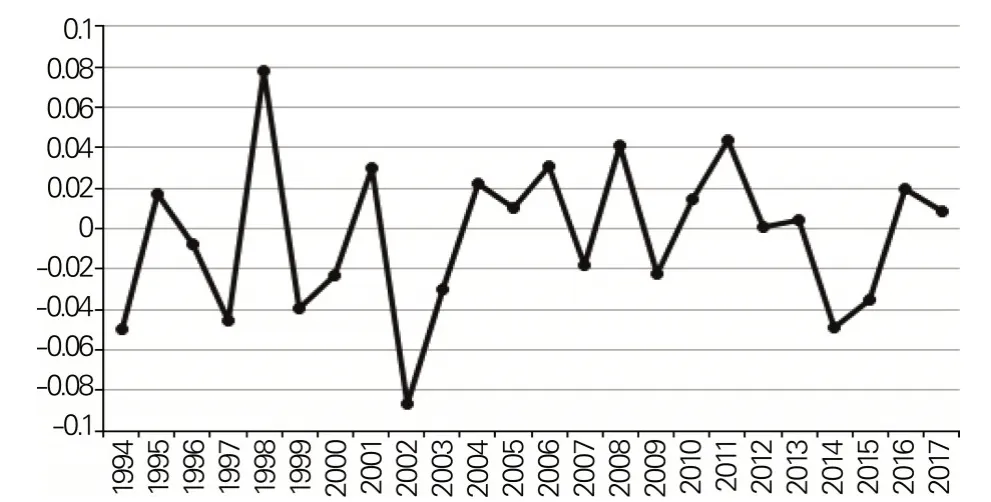
图3 河北省138个县级区域玉米单产波动率的均值变化情况
(二)基于混合数据的费率厘定
基于信度优化的数据混合法,首先对河北省138 个县级区域两两之间的RSV 序列进行K-S 检验,为每个区域确定混合数据的样本来源。由于涉及区域个数较多,此处仅以2017 年河北省玉米种植面积最大的宁晋县(位于河北省邢台市)为例,分析该县与河北省其他区域的数据同分布情况。利用MATLAB 编程,计算得到宁晋县与河北省其余137个县级区域K-S检验的p值,p取值范围与对应的县级区域个数如表1所示。
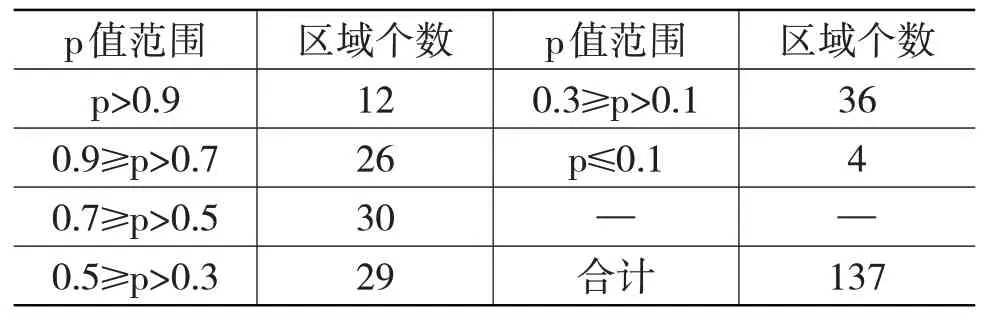
表1 宁晋县与河北省其他县级区域K-S检验的p取值范围与对应的区域个数
可以看出,在0.1 的显著性水平下,与宁晋县玉米单产RSV 序列具有同分布的区域个数有133 个,但大部分区域的p值较低,低于0.5的区域个数有69个,低于0.7 的区域个数有109 个,p 值高于0.9 的区域仅有12 个,占区域总个数的8.76%。基于上述数据求解信度优化模型[式(6)]可得到与宁晋县进行数据混合的区域,包括灵寿县、赞皇县、迁安市、卢龙县、成安县、磁县、魏县、广宗县、南宫市、蠡县、献县、安平县等12 个区域。按照条件信度水平从高到低排序,宁晋县玉米单产期望损失估计的条件信度水平随区域个数增加的变化情况如图4所示。
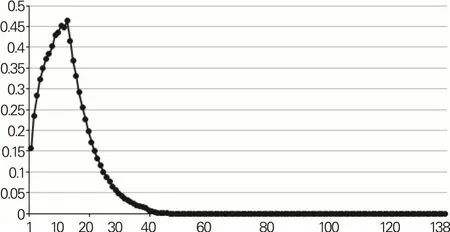
图4 条件信度水平的变化情况
从图4 中可以看出,利用本文设计的区域数据混合方法,随着合并的区域数的增加,条件信度水平呈现先增加后降低的变化趋势,这与图1 的分析结论一致。更进一步分析可知,若只基于宁晋县的样本数据,利用经验费率法,其玉米保险费率估计值为2.49%,估计值的信度水平为15.64%,数据混合上述12 个区域后,宁晋县玉米保险费率估计值变为2.77%,条件信度水平达到最大值46.40%,大幅度提高了宁晋县玉米保险费率的信度水平,费率具有更大的稳定性和可靠程度,仅利用宁晋县样本数据估计得到的2.49%很可能低估了玉米保险费率。利用MATLAB 编程计算得到138 个区域玉米保险费率及信度水平,限于篇幅本文仅列出保定市(2017 年河北省玉米产量最高的地级市)各县级区域的计算结果,如表2所示。
从表2的估计结果可以得出如下主要结论。
(1)利用混合数据方法横向扩大样本量,可提高费率估计的信度水平。除个别县级区域(博野县)外,保定市各区域费率厘定的平均条件信度水平从0.1852 提高至0.4113,提高了122%,不同区域信度水平的提高程度存在较大差异,标准差为0.0996,变异系数达到44%,其中信度水平提高最大的是阜平县(提高了279%),最小的是望都县(提高了15%)。
(2)在费率厘定过程中,按照条件信度水平最高原则,不同区域能够横向扩大的样本量具有较大差异。阜平县能够将23 个区域的数据混合利用(样本量增加了22倍),高阳县和曲阳县仅能够将2个区域的数据混合利用(样本量仅增加了1 倍)。其主要原因是部分区域与其他区域同分布的概率较低,例如博野县与其他县级区域同分布检验最大的p 值仅为0.38,因此该县与任何区域混合都会降低费率估计的条件信度水平,因此仅能使用本身的样本数据进行费率估计。
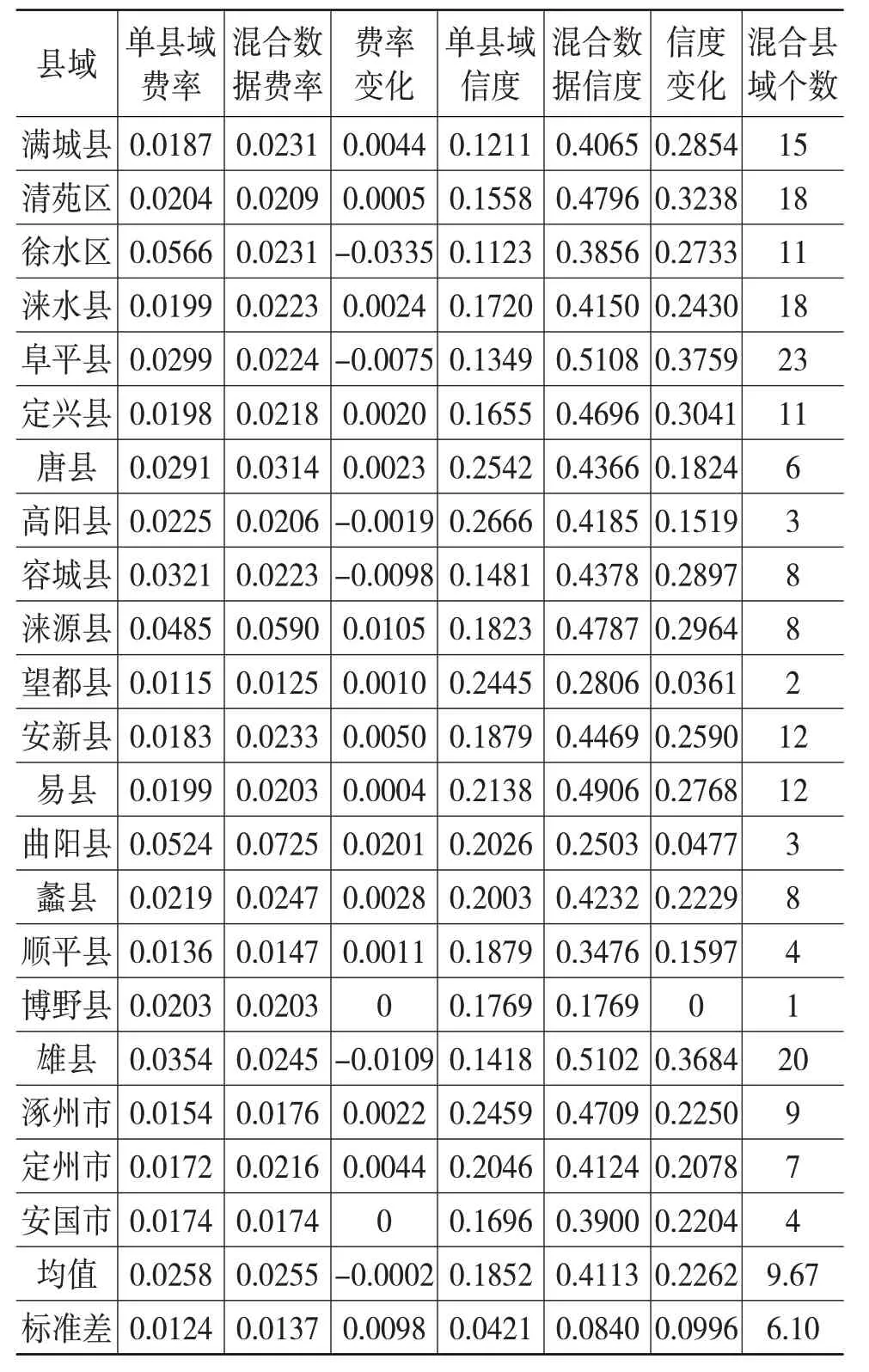
表2 保定市各县级区域玉米保费测算结果
(3)利用单区域样本数据厘定费率可能存在一定的估计偏差。从保定市21 个县级区域(博野县暂不具有可比较性)玉米保险费率的厘定结果来看,若基于单个县级区域样本估计费率,则徐水、阜平、高阳、容城和雄县等5 个区域可能高估了玉米灾害损失风险,造成保费定价偏高,费率偏高最多的区域为徐水区(差额为0.0335);其余15 个区域则可能低估了玉米灾害损失风险,造成保费定价偏低,费率偏低最多的区域为曲阳县(差额为0.0201);只有安国市的费率估计结果未发生变化,但在混合数据方法下,安国市费率估计的信度水平从0.1696 提高至0.3900,提高了0.2204。
(4)玉米保险费率存在较大区域差异。基于混合数据方法估计各区域的费率均值为0.0255,标准差为0.0137,变异系数达到53.73%,曲阳县的费率最高为0.0725,望都县费率最低为0.0125,最高费率为最低费率的5.8 倍。费率的差异性说明在玉米保险运作过程中,需要针对不同区域制定政策和承保方案,而不能实行“一刀切”。
(5)尽管费率厘定的信度水平有所提高,但整体水平仍然较低,保定市所有县级区域费率厘定的平均信度水平仅为0.4113。主要原因是本文仅利用了河北省的县级区域数据,能够选择的数据同分布区域较少,若基于全国县域数据进行费率厘定,则理论上可得到信度水平更高的估计结果。
五、结论与政策建议
(一)结论
为更好地解决我国农作物保险费率厘定中经验数据不足造成的问题,本文通过“借力”其他地区同分布数据横向扩大样本量,在扩大样本量的过程中对农作物灾害损失期望估计的信度水平和不同区域数据同分布的概率进行了综合考虑,提出了条件信度水平的概念,建立了农业保险费率估计的条件信度优化模型,分析了目标函数的变化规律,并以河北省为例,对其县级区域玉米保险费率进行了测定。
从河北省县级区域玉米保险费率厘定的结果来看,通过“借力”其他地区同分布数据横向扩大样本量,能够提高费率厘定的条件信度水平。以保定市为例,其县级区域保险费率信度水平的平均值从0.1852 增加至0.4113,提高了1.22 倍,基于单区域样本估计的费率既可能偏高也可能偏低,影响到保险市场的均衡状况,并且玉米保险费率存在较大区域差异,需要针对不同区域制定政策和承保方案。
(二)政策建议
1.加快完善农作物生产条件和单产数据库
高信度水平农作物保险费率的估计是农业保险可持续发展的基础和前提,本文提出的数据混合方法在一定程度上能提高费率估计的精准度,但数据混合后费率厘定的信度水平仍然较低。从本文的实证结果可以看出,当农作物生产条件相似和单产数据分布相同时,样本数据越多,费率估计的信度水平越高。我国有2800 多个县级区划,改进本文的混合数据方法,将具有相似生产条件(包括气象环境、生产资料、农户特征等)的县域进行数据分布匹配和混合,利用更多的区域数据样本,可更大程度地提高费率厘定的信度水平。
2. 制定基于疫情的支持政策,确保农业保险市场的稳定
突如其来的新冠肺炎疫情对国民经济的各行各业的发展都造成了影响,给农业保险的宣传、承保、查勘定损、保险服务以及灾害赔付等实际运作环节造成困难,降低了农户参保的积极性,提高了农业保险机构的运行成本。为更好发挥农业保险稳定农业生产、分散风险和保障农户收入水平的重要作用,需要定量分析疫情对农业保险的影响,适当调整保费补贴、税收优惠等政策,以减小疫情的冲击,维持农业保险市场的稳定。
3. 以高质量发展为目标,创新农作物保险费率厘定方法
近年来我国农业保险越来越受到党中央和国务院的重视,连续17 年的中央“一号文件”中都对农业保险工作进行了部署。2019 年中央全面深化改革委员会第八次会议审议通过了《关于加快农业保险高质量发展的指导意见》,其中专门强调要“完善保险费率拟订机制”,实现保险费率动态调整和“实现地区风险的差异化定价,真实反映农业生产风险”。因此亟须出台鼓励政策和措施,激励保险机构和科研人员创新多种方法提高风险估计和费率厘定的信度水平,为农业保险高质量发展提供实践和理论基础。

