堆芯计算的框架方法及其原型软件NAC4R的设计1)
明平洲,刘 婷,李治刚,尹 强,芦 韡,刘 东,曾 辉,余红星
(中国核动力研究设计院,四川 成都 610213)
随着并行计算技术发展以及电子计算机硬件性能的提升,反应堆工程领域具备研制较多大规模并行软件的条件。并行计算联合反应堆计算程序在高性能计算平台上的高效应用成为科研设计和工程应用的研究热点之一,它们从多个角度来提升核反应堆工程计算的效率和应用更多精细的模型[1,2]。伯克利并行实验室提出的Dwarf导则将并行软件的编写按照行业进行抽象,总结出并行模式设计,并在研究中针对蒙特卡罗中子输运计算形成了底层的框架软件[3]。核能领域的CASL等项目也将并行工具和底层算法进行整合,形成适用于大规模集群计算机的软件框架,并应用于工程耦合软件的研发[4,5]。框架方法的实质便是基于复用构件和软件结构进行软件的开发。框架方法的共性研究在著名的FLASH研究文献[6]中早期被总结为两种技术路线:
1)先设计和开发框架,然后逐步添加求解器和其他计算能力;
2)围绕小的求解器或专业应用进行持续研发,最终发展成为大型专业软件。
第一种技术路线方面,桑迪亚国家实验室研发的Trilinos是用于大规模工程和科学问题求解的软件框架。该计算框架集成了较多知名软件包,提供了丰富的数值计算功能;PETSc由阿贡国家实验室维护,提供多个适用于并行计算的线性和非线性数值求解器和功能模块;日本通过建立大规模并行数值计算技术研究小组,在京超级计算机上研制大规模的高性能数值软件KMATHLIB,与底层AICS硬件紧密结合[7];Charm++是由Illinois大学基于C++编程语言研制的并行面向对象编程语言,它将集群计算机的处理器核心虚拟化[8]。第二种技术路线方面,PPM围绕着物理学科的数值计算特点,研制了位于底层并行计算环境与学科应用之间的抽象中间件,减轻并行软件的研制难度[9]。以上基于框架方法的研究思路在堆芯计算领域,尤其在国内尚处于无统一标准的局部应用阶段(例如中国工程物理研究院的JASMIN软件),且缺乏细致的程序设计和对应的理论模型。
围绕着堆芯计算软件的应用重点,论文描述了适用于堆芯计算的框架原型软件NAC4R的设计和初步编程实现,并列举抽象程序的验证和实际屏蔽输运计算软件Hydra-SN3D的重制工作来说明框架方法的有效性。
1 理论和设计
数值计算与并行计算环境可以按照不同层次进行融合[10]。例如在计算科学领域,中间件的概念来源于分布式计算技术,它基于网络计算平台上部署的分布式计算环境,用于提供开发工具和公共服务,从而支持分布式通信应用。本文提及的框架方法则侧重于数值计算的功能设计,同时包含部分中间件的内容以便集群计算机的数据通信,重点关注数值计算内数据的传递和代数运算。NAC4R作为框架方法的原型设计,其研制过程将专业应用范围限制在堆芯计算,且运行平台仅考虑内部封闭的集群计算机系统,所以与硬件的配合程度应单独予以考虑。
1.1 理论说明
框架方法映射至软件系统的不同层次,NAC4R的基本结构框图如图1所示。

图1 NAC4R的结构框架Fig.1 The structure of NAC4R
该设计提供多种基础计算功能,然后利用Python接口层来进行自动化处理和提供外部应用函数接口。现阶段在原型阶段对基础计算功能的模块进行如下分类:
1)基础数据模块,对控制和计算所用的数据进行合理表示,兼顾串行情况和分布式内存并行情况;
2)常用功能模块,提供基本的非数值计算操作,例如数据封装、快速排序、查找和图分区等功能;
3)基础线性代数操作,例如对BLAS函数接口规范、LAPACK函数接口规范提供包裹函数,便于直接使用FORTRAN函数。后续在接口规范一致的前提下也可以编程实现适用于特定并行硬件的基础线性代数功能;
4)并行数据结构模块,它由1)进行派生,基于著名的Epetra模块,在分布式内存环境下对数据进行合理表示和存储[11];
5)线性方程组求解,现阶段仅需提供Jacobi、Bi-CG、GMRES和LU分解的求解器,实现求解功能和考虑初步的健壮性,基于著名的Aztec模块进行编程实现[12];
6)输入输出模块,对框架内部的输入输出功能进行编程实现,关注文本文件和二进制文件,同时提供框架内部固定的计算数据存储格式;
7)事件追踪模块,提供对计算过程的时间线统计和计算时间分析,便于引入TAU等工具;
8)基础数值计算模块,提供基本的数值计算操作和数值函数,例如伽马函数,勒让德多项式展开系数,线性求积组等功能。
因此,NAC4R的基础计算功能现阶段由8个模块组成,并强调使用C/C++语言和Fortran语言进行混合编程实现计算核心,一方面便于C/C++语言实现控制和封装等管理特性,另一方面便于Fortran语言实现高效数值计算和利用已有的底层计算核心,例如BLAS、LAPACK等第三方内容。通过以上设计可以归纳出,NAC4R与框架方法的联系体现在多项计算内容的抽象上。
(1)数据的表达
在集群计算机内部,数据结构主要分为三类:原语类型、复合类型和抽象数据类型。各种堆芯计算相关的具有物理意义的数据便由这些数据结构进行承载和存储。NAC4R一方面提供专用的数据结构,诸如双向链表、B-tree、红黑树以及图,另一方面也根据堆芯计算的特点,强调数据有效的组织逻辑,表述为区域拓扑、粒子、网格等对象。这些数据的表达在NAC4R内部由类部件或者函数接口这种模块形式来提供使用。
(2)数据通信
在分布式内存情况下实现高效的数据通信。现有的集群计算机在处理器核心之间主要使用MPI消息传递模型进行数据通信,为了开发用户层面上函数接口的统一性和适应扁平化设计,并不直接使用MPI提供的函数,而是进行包裹函数库(Wrapped Function Library)的研发设计,一方面减少输入形参和实现功能的组合和统一管理,另一方面固定函数接口,使得包裹函数内部可以灵活更改,以适应不同的硬件平台和更新或者替换底层的MPI库(见图2)。

图2 包裹层示意图Fig.2 Schematic of the wrapping layer
这种设计思路在PETSc、Trilinos、KMATHLIB和较多的框架软件中均有体现,按照分布式通信集中管理的原则,NAC4R内的数据通信通过管理功能、数据转换功能、通信区域分割等内容进行实现,它涉及MPI分布式内存并行和OpenMP或多线程共享式内存并行。
(3)文件I/O
在MPI-2规范中引入的并行I/O,也称为MPI-IO,它是NAC4R数据通信模型中关于分布式文件读写的基础。为了减小问题的复杂度,NAC4R对文件的读写仅仅针对二进制文件,并不针对文本文件(文本文件可以通过转换接口来生成二进制文件),且NAC4R也使用和扩展了Fisher所提出的SDF文件格式来减小数据存储和传递的复杂性[13]。
(4)数值求解器
NAC4R的数值求解部分针对具体的堆芯计算特点,现阶段已实现线性方程组Ax=b和非线性方程组的部分求解方法,例如围绕Jacobi、Bi-CG、GMRES和LU分解的理论和算法进行设计和实现。为了提升适应性,当矩阵规模较小或精度要求较高时,使用直接法的接口更为有效。
1.2 编程考虑
原型软件NAC4R内存在着面向结构和面向对象的软件设计,考虑到应用需求,它自身存在着配置文件,可以指定具体的计算任务和集群计算机的资源等信息实现独立运行。在NAC4R的编程实现过程中应考虑三种应用情况。
1)直接在上面集成专业应用的求解器,构成完整的专业软件;
2)使用NAC4R提供的部分模块,以函数库的形式进行重用;
3)复用NAC4R的程序代码,并利用提供的自动化功能进行并行性能预测和收集计算信息。
1.3 原型研制步骤
基础模块的开发为第一阶段,体现为NAC4R在研制过程中实施单元测试,然后开发相应的示例程序和脚本语言包裹层。
第二阶段对实际的堆芯样本程序进行应用和分析,本文选取结构化网格条件下的三维离散纵标法的并行算法进行应用研究。针对其中的径向扫描并行算法部分,样本程序被解读和分析,并在NAC4R原型软件中快速进行重新开发,理解核心并行求解算法的编写流程和效率提升模式(见表1)。
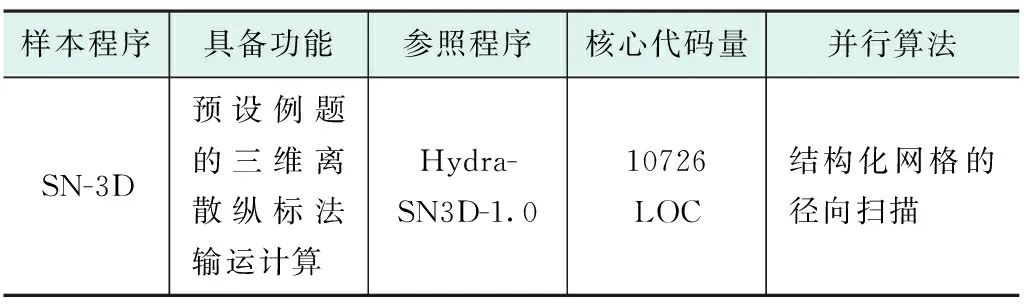
表1 样本程序Hydra-SN3D的信息
第三阶段是持续改进原型软件NAC4R,并扩大应用范围,对新的堆芯计算特点进行特征识别,即在NAC4R内部集成新的并行算法和共性计算内容。
1.4 离散纵标法
美国LANL实验室研制的一系列离散纵标程序是SN方法的起源,北京应用物理与计算数学研究所前期围绕中子输运SN算法开展了多方面的研究,并重点介绍二维中子输运方程SN算法的研究与应用情况[14]。2010年美国LANL实验室的技术报告中宣讲了走鹃超级计算机上运行的SN输运程序Sweep3D,它作为PARTISN中子输运程序的缩减版本,可以计算XYZ三维笛卡尔坐标系的几何系统,使用二维处理器网络结构来匹配几何的分块网格,从多个层次上实施并行来加速SN算法的求解[15]。离散纵标法的形式通常由波尔兹曼输运方程的离散纵标形式进行建模,可以反映中子或光子的辐射效应。
Ωm·Img+(σA+σS)Img
(1)
辐射通量Img(x,y,z)按照能群、角方向进行离散化,公式表明沿着一个特定方向Ωm辐射通量将发生的变化,求解过程便是定量获得此变化趋势。计算时只对选定的若干个离散方向Ωm对中子输运方程进行求解。从中子输运方程求出φ(r,E,Ωm)后,关于方向Ω的有关积分则用数值积分来近似表示。
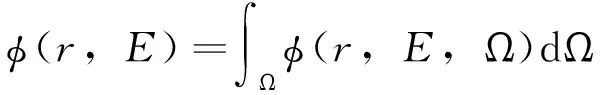
(2)
式中,求积系数ωm、离散方向及其数目取决于计算精度的要求(SN方法,又写作SN)。此处下标N表示方向向量在某个坐标方向上(例如XYZ三维笛卡尔坐标系的某个坐标轴方向)的离散点数目。近期中国核动力研究设计院和西安交大联合研制Hydra-SN3D是类似于DORT核心求解器的离散纵标法程序。程序将整个方程抽象为矩阵系统进行求解,这种完整性更贴近于复杂系统的模拟和仿真。假定输运算符为Η,裂变算符为Γ。
Ηφ=Ω·
(3)
(4)
根据公式(3)和(4)的算符定义,离散纵标法的源迭代求解算法为:

Input:ϕ0,v∑f,∑s,∑tOutput:keff,ϕS=Γϕ;while|k-kold|kold≥εkor||S-Sold||||Sold||≥εϕdo Hϕ=S Sold=S S=Γϕ k=
对离散纵标法的框架方法实践将基于上面描述内容实施抽象和编程实现。
2 抽象程序和数值实验
框架方法同时强调抽象,为了有效在NAC4R内部实现对样本程序的应用或研究,可以参照代理程序SNAP的研究思路[16],根据问题域本身的特征进行抽象(本文强调堆芯计算)。一方面抽象其中的核心计算部分,按照NAC4R提供的程序部件和结构进行重写;另一方面使用数学模型来模拟真实软件的行为,研究新的模型、算法等。
2.1 性能预测
堆芯计算的一次完整计算可以按照功能和先后次序进行分解,总可以形成图3所示的多个计算任务构成的网状结构。
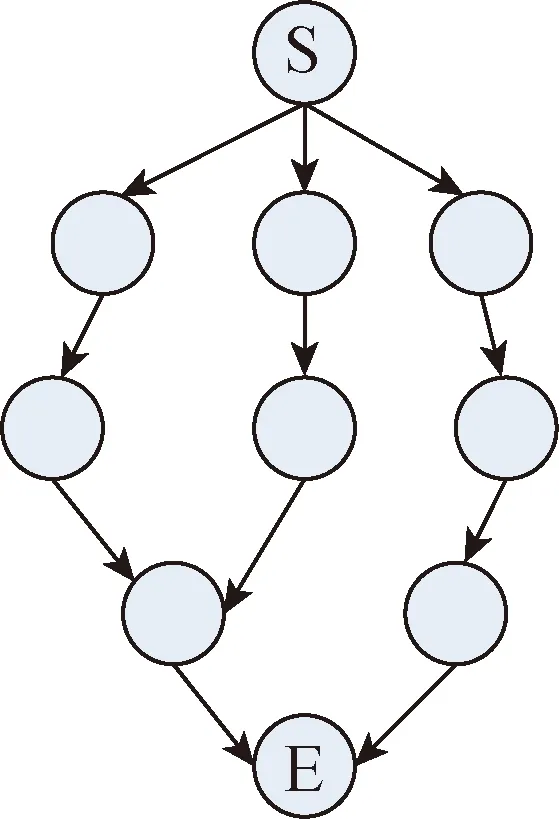
图3 计算任务的网状结构Fig.3 Mesh structure for computing tasks
此时每个计算任务可以使用一个进程或线程代表的计算资源完成计算,然后发送数据到它的后继,其后继在接收到所有所需数据之后开始计算。在数学上,这种互联网状结构可以通过有向图或者Petri网进行表达和研究。有向图是由一组定点和边(V,E)进行定义的数学模型,当有向图中不存在循环结构时,有向图又被称为有向无循环图,它仍然遵循有向图的各种定理,例如反向后序序列等价于图模型中的拓扑排序,反映了各个计算任务的一种调度关系。当有向无循环图的连接边E不存在权重值时,可以直接由有向图对应的矩阵M进行调度算法的设计。
1)Mi,j在初始情况下为0,当单元被调度完成计算后,可以置Mi,j为1;
2)Mi,j(i≠j)表明了单元j依赖的前驱单元,如果Mi,j≠0,则单元j的调度需要等待单元i完成计算。
离散纵标输运计算的径向扫描计算具备图4所示的流水线结构,它在SN输运计算过程中可能由多进程对较大的分块区域按照此互联关系进行并行求解,也可能由多线程对分块区域内部的网格按照此互联关系进行并行求解,前者会产生进程之间的数据通信开销,后者则共享数据内存,只存在着计算的先后次序和多线程的管理开销。

图4 SN方法的流水线结构Fig.4 Pipeline of the SN method
假定每个网格区域的体积一致时,此时每个网格区域的计算任务的计算量相同,当数据量较小且不考虑数据通信时,对应于多线程并行情况,此时理想并行性能(加速比)为:
(5)
理想性能的取得需要计算资源(进程或线程)满足≥min{i,j}。当计算资源并不充足时,可以根据上述抽象和NAC4R提供的并行性能预测工具生成不同概率分布的输入,模拟资源数的增长与实际的并行性能,获得指导性建议来辅助并行编程。以I=50,J=50为例,可以使用工具模拟,按照时间片轮转的方式得到以下的运行时间趋势。
图5显示的趋势表明每个网格区域的计算量相同,且不考虑数据通信时,当计算资源在10(十个进程或线程)以内时,该例题规模下并行所带来的增益最为明显。考虑到预测的复杂性,还可以采用Petri网数学模型对更为复杂的情况进行性能预测,例如当每个网格区域的计算量不相同,考虑数据通信之后的多进程并行性能。2.1节解释的框架方法反映的是一种程序抽象的能力,并行算法的性能预测是一种用途。
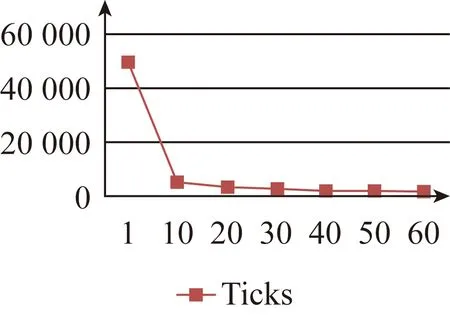
图5 SN径向扫描的并行性能预测Fig.5 Parallel performanceprediction of radial scanning
2.2 离散纵标法的径向并行扫描
与2.1描述的抽象保持一致,真实的离散纵标法的扫描算法在每个卦限内每个离散方向均需要遍历扫描各个网格,它在结构化网格的条件下应用KBA并行扫描算法。此时求解过程对应于通量矩的线性系统的代数运算。
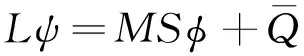
(6)

L——差分输运算符;
M——通量矩离散化算符矩阵;
S——散射矩阵。
待求解对象ψ代表角通量,φ为通量矩。结构化网格情况下KBA扫描计算的实质是求解L-1,它将三维网格进行区域划分,假设总的网格在每个方向上为(I,J,K),各个区域(Ia,Jb,K)被映射至每个进程计算任务进行并行求解。此时每个卦限内的各区域XY方向上的扫描计算由多层循环结构表示,它的算法描述为:

I,J,K←0,1,2for k in d_begin[K]:d_end[K] ϕup,j←ϕin for j in d_begin[J]:d_end[J] for i in d_begin[I]:d_end[I] ϕpsi←ϕup callT(i,j,k,ϕpsi) end for ϕup←ϕpsi end for ϕout←ϕup,j end for ϕout←ϕup,k
上述扫描计算过程中,外推模型的计算子函数T具备独立性,仅仅与网格序号(i,j,k)相关,通量矩变量φup、φpsi等存在着先后依赖关系。对于该流水线并行的并行算法,可引入全局标志位来辅助流水线结构的执行,此时的循环结构使用OpenMP多线程并行的算法可以设计为:

#pragma omp parallel forfor j in d_begin[J]:d_end[J] for i in d_begin[I]:d_end[I] wait(done[j][i]) ϕpsi←ϕup call T(i,j,k,ϕpsi) done[next(j)][i]=1 end forend for
框架方法在原型软件NAC4R中单独提供一类机制来统一这种流水线结构的执行。一方面由于循环结构并行算法的不恰当编程实现将造成性能的恶化,另一方面以上算法结构较难高效和正确编写成功。NAC4R统一使用OpenMP提供的omp_set_lock和omp_unset_lock操作提前分配和管理互斥数据结构,便于OpenMP多线程在流水线结构下并发运行。计算用户只需要编写循环结构本身,将计算和数据表示相互独立,也便于后续保留效率较高的程序编写模式。表2统计了编译优化等级为-O0时的数值实验计算效率,两个预设例题的计算结果在样本程序、NAC4R改写之后的程序及其并行版本均保持一致。

表2 预设例题的计算时间统计
两个例题的单进程计算效率得到了较大提升,且对于每个基准例题,按照3.1节提供的预测信息,对每个进程使用8个线程实施的多线程并行均起到了接近图5所示的加速效果。这给后续引入进程和线程多级并行的策略带来信心。
表3则统计和对比了不同编译优化等级下NAC4R内重制的离散纵标法模块的计算时间,如果简单按照前面列出的全局标志位来编写OpenMP并行算法,O2优化等级将无法得到一致的数值结果。NAC4R内部统一提供的多线程锁机制的管理方式确保了计算结果保持不变,且表中数据表明高编译优化等级下流水线扫描结构仍然可以使用OpenMP多线程来提升计算性能。

表3 不同编译优化等级的预设例题计算时间统计
样本程序Hydra-SN3D在NAC4R内部的重制工作前后共花费2个月,共3个人力,其中主要程序开发人员仅花费1个月便完成Hydra-SN3D软件的编制和测试。NAC4R这种统一结构的框架方法及其编程理念有利于程序的研制、改写或重组,可复用的工程应用核心就在于提供了较多共性计算功能和使用单个模块部件及其组合这种形式来组织数值计算内容。原型软件NAC4R内部存在较多可复用的程序片段,它们是以往并行软件研制经验和模式的总结,使得开发用户花费更多时间对问题进行抽象,匹配已有模式,从而缩减编写程序的时间。
3 结论
随着应用的深入和计算硬件的改善,超大规模集群计算机下堆芯计算软件的呈现将产生较大变化。NAC4R原型软件作为框架方法的研究思路在本文进行了介绍,通过讨论,得到如下结论。
1)框架方法可以取得软件复用的目标,堆芯计算经过抽象来适应已有的模式或基础计算功能可以简化数值程序的编写流程,且便于并行算法相关内容的分析。提出的NAC4R原型软件对框架方法的实例化初步可行,从基础功能上给出了较多计算的理论来源和编程实现考虑。
2)离散纵标法的屏蔽输运程序Hydra-SN3D在NAC4R内被重新抽象和编程实现,通过数值实验和统计数据论证了框架方法应用于堆芯计算的可行性和有效性。
后续将进一步对原型软件进行发展,以适应更多堆芯计算内容,例如非结构化网格的离散纵标法程序和两相流仿真程序等,扩大框架方法的适用范围和提炼其中的并行模式。

