高含水期油藏加密井位高效优化方法
刘晨 潘岳 王凯 李竞 刘凡 唐莎莎 周文胜


摘 要:为实现加密井位的快速优化,从油藏实际出发,基于最优化原理,以实现油藏可动油储量的均衡驱替为目标,建立高含水期油藏加密井位优化数学模型,并基于油藏工程理论建立油藏开发指标的快速计算方法,在此基础上,结合智能优化算法实现加密井位优化数学模型的高效求解,从而形成了一套高含水期油藏加密井位快速优化方法。A油田应用实例表明,新方法优化的井位明显优于人工设计井位,通过新方法井位优化使得储层平面驱替更加均衡,累积产油量增加了12.6×104 m3,增加3.29%,验证了该方法实际应用的可行性。该方法求解过程简洁,无须调用数值模拟器,大幅缩短计算时间,具有可实施性强、计算简便快捷的优点,在高含水油田具有广泛的应用前景。
关 键 詞:高含水油田;井位优化;开发指标计算;智能优化
中图分类号:TE357.1 文献标识码: A 文章编号: 1671-0460(2020)11-2536-05
Optimization Method of Well Placement in High Water Cut Reservoirs
LIU Chen 1,2 , PAN Yue1,2, WANG Kai1,2, LI Jing1,2, LIU Fan1,2, TANG Sha-sha1,2, ZHOU Wen-sheng1,2
(1. State Key Laborator of Offshore Oil Exploitation, Beijing 100028, China;
2. CNOOC Research Institute Ltd., Beijing100028, China)
Abstract: In order to realize the fast optimization of infill well location at the reservoir in high water cut stage, the mathematical model of infill well location optimization in high water cut reservoir was established based on the principle of optimization to realize the balanced displacement of reservoir movable oil reserves. The fast calculation method of reservoir development index was established based on the theory of reservoir engineering. On this basis, the infill well location optimization was realized by combining the intelligent optimization algorithm. The example showed that the well placement optimized by the new method was obviously better than that designed by man. The well placement optimized by the new method made the reservoir plane displacement more balanced, and the cumulative oil production increased by 1.26×105 m3, which proved the feasibility of the practical application of the method. This method is simple in solving process, does not need to call numerical simulator, which greatly shortens the calculation time. It has the advantages of strong feasibility, simple and fast calculation, and has a wide application prospect in high water cut oilfields.
Key words: High water cut oilfield; Well placement optimization; Development index calculation; Intelligent optimization
高含水期油藏受地质因素与开发因素的双重影响,储层非均质性更加复杂,剩余油认识难度大,如何合理确定调整井位、改善开发效果是一项重要课题。传统的开发调整措施已不完全适应水驱油田开发的需要。合理井网及注采策略是水驱油田开发中最关键的问题之一,井网部署和注采策略的确定是一项复杂的系统工程。为了实现加密井位的快速优化确定,国内外学者建立了多种井位优化方 法[1-14]。从井网加密研究的现状来看,目前的井网加密优化方法大概可以分为常规井网加密方案优选方法、基于优化理论的井网加密优化方法以及矢量井网优化方法。传统的井网加密方案优选方法往往依赖于油藏工程师的经验,人工设计多套方案进行对比优选,受人为主观影响较大,无法保证得到真正意义上的最优方案;基于优化理论的井网加密优化方法将井网加密设计抽象为数学上的最优化问题,通过耦合油藏数值模拟器和优化算法求解得到最优的井网加密方案,这类方法的计算量巨大,受限于数值模拟器的计算效率以及优化算法的选取;矢量井网优化方法通过开发井网井距的优化部署,使得井网参数与地质矢量参数相协调,最终达到均衡水驱最大化的目标,这类方法目前仍处于起步阶段,目前该方法只适用于单层油藏,无法应用于海上油藏多层合采开发条件下的井网加密矢量优化。目前方法主要通过耦合数值模拟器与优化算法实现,通过优化算法进行井位调整寻优,依靠数值模拟器计算不同井位设置下的开发指标,由于需频繁调用数值模拟器模拟开发指标计算,这种方法计算量大、耗时长、对设备要求高,难以满足实际油藏的应用需求。针对以上问题,本文从油藏实际出发,基于最优化原理,以实现油藏可动油储量的均衡驱替为目标,建立了高含水期油藏加密井位优化数学模型,并基于油藏工程理论建立了油藏开发指标的快速计算方法,在此基础上,结合智能优化算法实现了加密井位优化数学模型的高效求解,从而形成了一套高含水期油藏加密井位快速优化方法,实现了实际油藏加密井位的快速自动优化。
1 数学模型建立与求解方法
加密井位优化是通过不断调整加密井的井位,使得油藏驱替更均衡,从而改善水驱油藏的开发效果,提高油田经济效益。加密井位优化问题是一个最优化问题。油藏加密井的方位、井斜、井身长度等参数,受到实际钻井平台及钻井技术的约束,因此,油藏加密井位优化问题是一个有约束的最优化问题。
1.1 加密井位优化数学模型
加密井位优化的目标即通过优化加密井的跟端坐标和趾端坐标,实现油藏最大化均衡驱替。对于均匀油藏,油藏均衡驱替程度可通过含水饱和度的方差进行表征[15-16]。对于实际油藏,需考虑储层的各向异性,可先对含水饱和度进行标准化处理,再基于标准化含水饱和度的方差进行油藏可动油储量均衡驱替程度的表征。油藏饱和度分布受储层岩石物性、流体物性、井网参数和工作制度等一系列因素的影响。在井位优化问题中,认为除了各井井位外,其他参数均为一定的,此时饱和度为关于井位的函数。因此,加密井位优化方程可表示为:
; (1)
。 (2)
式中:f—目标函数,表征油藏可动油储量均衡驱替程度;
X—加密井位优化变量矢量,包括加密井的跟端坐标(xh,yh,zh)
及趾端坐标(xt,yt,zt);
Swp—各注采方向的含水饱和度;
Swi—各注采方向的初始含水饱和度;
Sor—各注采方向的残余油饱和度;
—平均含水饱和度;
—各方向初始含水饱和度平均值;
n—注采連线总个数。
基于井轨迹控制和钻完井要求,加密井位优化过程中的约束条件主要包括油藏边界约束、井身长度约束、井斜角度约束及方位角度约束。其约束条件可表示为:
。(3)
式中:Ω—油藏边界范围;
Lmax—允许最大井身长度;
θ—井斜角,可根据加密井井位的跟端坐标和趾端坐标计算得到;
θmin—允许的最小井斜角;
θmax—允许的最大井斜角;
ψ—方位角,可根据加密井井位的跟端坐标和趾端坐标计算得到;
ψmin—允许的最小方位角;
ψmax—允许的最大方位角。
1.2 求解方法
上述优化模型求解过程中涉及储层含水饱和度的实时计算。通过调用数值模拟器耦合求解计算量大,影响效率。本文基于B-L水驱油理论[17-19],建立了含水饱和度实时计算的油藏工程方法,可直接快速计算不同生产时间下各注采连线上的含水饱和度。
根据水驱油理论,注采井间渗流关系可以分为两种情况:油井见水前,注水井到生产井间可分为油水两相区和纯油区;油井见水后,注水井到生产井间为油水两相区。因此,注采井间渗流阻力计算公式为:
。(4)
式中:rf—水驱前缘位置,m;
Kro—油相的相对渗透率;
Krw—水相的相对渗透率;
μo—油相的黏度,mPa·s;
μw—水相的黏度,mPa·s;
Swc—束缚水饱和度。
小层储层流体流量可通过注采压差和渗流阻力确定,计算公式为:
。 (5)
式中:Qi—第i小层的流体流量,m3·d-1;
Ki—第i小层的注采井间渗透率,10-3 μm2;
Ai—第i小层的横截面积,m2;
△p—注采井间生产压差,MPa;
—第i小层的平均视黏度,mPa·s;
l—注采井间距离,m;
Ri—第i小层注采井间渗流阻力,mPa·s·(μm2·cm)-1;
a—单位转换系数。
根据物质平衡原理,单位微元内水增加量与产油量的关系可表示为:
。 (6)
式中: —注采井间孔隙度;
fwi —第i小层含水率。
对式(6)进行积分,可以得到:
。 (7)
式中:rw —井的半径,m。
根据式(7)就可以得到不同生产时间下各注采连线上的含水饱和度。
通过迭代计算,得到最终各注采连线上含水饱和度,将其代入式(1)即可计算特定井位下的油藏均衡驱替程度。
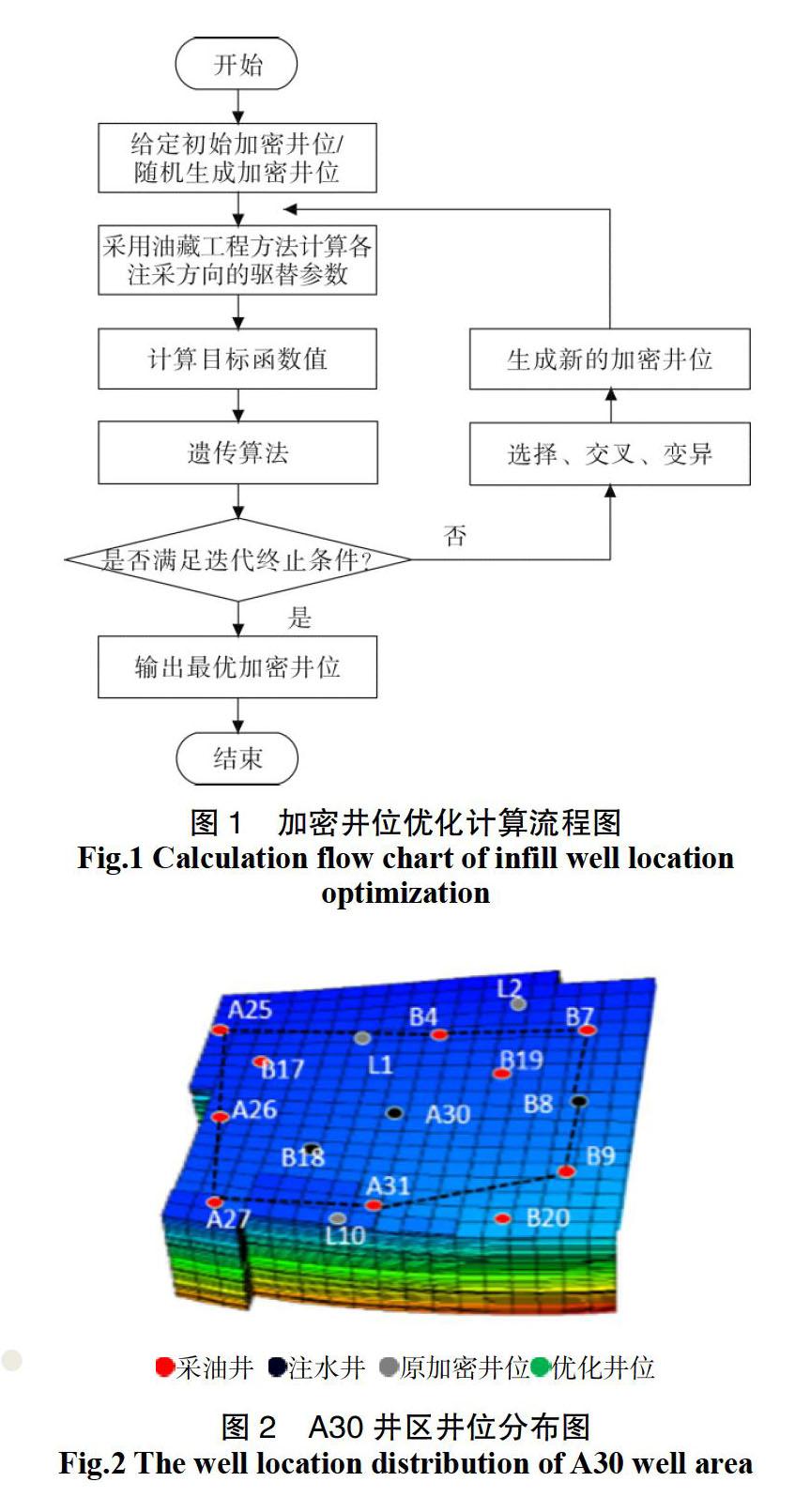
为了能够实现加密井位的自动寻优,采用智能优化算法对上述加密井位优化问题进行求解。遗传算法是一种典型的启发式随机搜索方法,通过模仿自然界的选择与遗传的机理来寻找最优解。它具有独特的运行机制和算法形式,在复杂问题求解中具有显著的优势。遗传算法在井网优化问题中有很多成功的应用,其解决优化问题时有如下特点:直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。遗传算法因其具有优良的全局寻优能力、自适应调整搜索方向、无函数连续性要求等诸多优点,已在各工程领域得到广泛应用[20]。采用遗传算法对加密井位优化问题进行求解,针对优化过程中的约束,采用惩罚函数方法对其进行惩罚处理。求解流程图如图1所示。
2 应用实例
A油田A30井区为三角洲前缘沉积,储层非均质性较强。纵向上看,该井区层间渗透率级差为2.21~384.08、突进系数为1.5~3.26、变异系数为0.3~0.82,其中60%的井变异系数>0.7,井组层间非均质程度极强;平面上看,平面渗透率级差为4.16~294.4、突进系数为1.49~1.36、变异系数为0.46~1.36,其中,58.3%的井变异系数>0.7,井组平面非均质性也较强。
该井区现有10口采油井,3口注水井(图2)。井区累计注水1.707×106 m3,注水厚度74.5 m,其中主要吸水层位2、4、6小层仅占总厚度的57.7%,累计吸水却达到了1.39×106 m3,占总注水量的81.4%,单层突进严重,受效油井含水率较高。井区综合含水率87.8%,采出程度仅为9%,开发效果较差。为改善该井区的开发效果,提出在该井区增加3口加密油井(L1、L2、L10),并人工设计了加密井位(图2)。为了能够更好地改善油藏开发效果,基于本文建立的方法对3口加密井井位进一步进行了优化,使之与油藏的非均质性相匹配,实现油藏的高效开发。
基于人工设计的加密井位为初始值,采用本文建立的方法进行迭代优化求解。由图3可知,基于初始人工设计的加密井位油藏均衡驱替程度为1.6,经过20次迭代优化后,新井位的油藏均衡驱替程度为1.8,提升了12.5%。
新井位与初始井位对比结果如图4所示。优化后的加密井位较初始加密井位均有所调整,L1井调整幅度较大,L2、L10井调整幅度较小。
对优化后加密井位与初始人工设计加密井位采用统一数值模拟模型进行了开发效果预测。结果表明,采用人工设计的加密井位15年后该井区的累积产油量为3.831×106 m3,而采用优化的加密井位15年后该井区的累积产油量可以达到3.957×106 m3,通过井位优化增加了1.26×105 m3的产量,累积产油量增加3.29%。从15年后的井区剩余油饱和度分布也可以看出,采用优化后的加密井位使得储层平面驱替更加均衡。见表1。
3 结 论
1)以油藏可动油储量的均衡驱替为目标,建立了高含水期油藏加密井位优化数学模型,并基于油藏工程理论和智能优化算法实现了高效求解,从而形成了一套高含水期油藏加密井位快速优化方法,实现了实际油藏加密井位的快速自动优化。
2)A油田应用实例表明,新方法优化的井位明显优于人工设计井位,通过新方法井位优化使得储层平面驱替更加均衡,累积产油量增加了1.26×105 m3的产量,增加3.29%。
3)该方法求解过程简洁,无须调用数值模拟器,大幅缩短了计算时间,具有可实施性强、计算简便快捷的优点,在高含水油田具有广泛的应用前景。
参考文献:
[1]王家宏. 多油层油藏分层注水稳产条件与井网加密调整[J]. 石油学报,2009,30(1):80-83.
[2]张凯,吴海洋,徐耀东,等. 考虑地质及开发因素约束的三角形井网优化[J]. 中国石油大学学报, 2015,39(4):111-118.
[3]鲍敬伟,李丽,叶继根,等. 高含水复杂断块油田加密井井位智能优选方法及其应用[J]. 石油学报,2017,38(4):444-452.
[4]FENG Q H, CHENH W, WANG X, et al. Well control optimization considering formation damage caused by suspended particles in injected water[J]. Journal of Natural Gas Science & Engineering, 2016, 151(2): 1037-1051.
[5]ISEBOR O J, DURLOFSKY L J. Biobjective optimization for general oil field development[J]. Journal of Petroleum Science and Engineering, 2014, 119(1): 123-138.
[6]NADERI M, KHAMEHC E. Well placement optimization using metaheuristic bat algorithm[J]. Journal of Petroleum Science and Engineering, 2017, 150(2): 348-354.
[7]CHENH W, FENGQ H, ZHANGX M, et al. Well placement optimization using an analytical formula-based objective function and cat swarm optimization algorithm[J]. Journal of Petroleum Science and Engineering, 2017, 157(4): 1067-1083.
[8]ISEBOR O J, DURLOFSKY L J, CRAURRI D E. A derivative-free methodology with local and global search for the constrained joint optimization of well locations and controls[J]. Computational Geosciences, 2014, 18(3-4): 463-482.
[9]EMERICK A A, SILVA E, MESSER B, et al. Well placement optimization using a genetic algorithm with nonlinear constraints[C]. 2009, SPE 118808
[10]孫致学,苏玉亮,聂海峰,等. 基于生产潜力的深水油田井位优化方法及应用[J]. 断块油气田,2013,20(4):473-476.
[11]LYONS J, NASRABA H. Well placement optimization under time-dependent uncertainty using an ensemble Kalman filter and a genetic algorithm[J]. Journal of Petroleum Science & Engineering, 2013, 109(9): 70-79.
[12]SAMPAIR M A, BARRETA C E A G, SCHIOZER D J. Assisted optimization method for comparison between conventional and intelligent producers considering uncertainties[J]. Journal of Petroleum Science & Engineering, 2015,133: 268-279.
[13]CHENH W, FENGQ H, ZHANGX M, et al. Well placement optimization for offshore oilfield based on Theil index and differential evolution algorithm[J]. Journal of Petroleum Exploration and Production Technology, 2018, 8(4): 1225-1233.
[14]郭武豪,江厚順,谢昊. 基于改进量子遗传算法的油田井位及数量优化[J]. 计算机测量与控制,2019,27(2):156-159.
[15]冯其红,王相,王端平,等. 水驱油藏均衡驱替开发效果论证[J]. 油气地质与采收率,2016,23(3):83-88.
[16]闫天雨,李玮,李建冰,等. 致密砂岩储层压裂裂缝扩展形态试验研究[J]. 当代化工,2020,49(1):14-18.
[17]姜汉桥,姚军,姜瑞忠. 油藏工程原理与方法[M]. 东营: 中国石油大学出版社,2006.
[18]秦同洛,李汤玉,陈元千. 实用油藏工程方法[M] . 北京: 石油工业出版社,1989.
[19]张建国,杜殿发,侯健,等. 油气层渗流力学[M]. 东营: 中国石油大学出版社,2009.
[20]MONTES G, BARTOLOME P, UDIAS A L. The use of genetic algorithms in well placement optimization[C]. SPE Latin American and Caribbean Petroleum Engineering Conference, 2001.

