双绳多层缠绕式提升机卷筒结构对钢丝绳张力差的影响

邓 勇,龚宪生,唐 涛,王海隆

(1.重庆大学 机械传动国家重点实验室，重庆 400044; 2.重庆大学 机械工程学院，重庆 400044)

面临我国浅层矿产资源开采殆尽的严峻形势，向地球更深部开采资源已成为我国的重要战略。目前我国矿山的平均开采深度大多在500 m左右[1]，而南非的开采深度已达3 000 m以上[2]。矿井提升机承担着联系井上和井下的作用，是连接地面与地下人员和物资输送的“咽喉设备”，井深大于1 500 m的超深矿井提升装备成为了深部资源开发的瓶颈[3]。现有的单绳缠绕式和摩擦式提升机已不能满足超深井重载、高效率和高安全提升的需要，双绳多层缠绕式提升是实现超深井提升的创新思路[4]。

双绳多层缠绕式提升机卷筒有左右两个缠绳区，两缠绳区的变形不同步会引起两钢丝绳缠绕周长差异，造成两钢丝绳的悬垂长度不同，罐笼在罐道的约束下，使得提升钢丝绳长度差导致张力差异。张力差严重时将危及提升系统安全，《煤矿安全规程》[5]明确规定:多绳提升的任意一根钢丝绳的张力与平均张力之差不得超过±10%，因此探明卷筒结构对钢丝绳张力差的影响规律具有重要的理论及工程意义。

现有研究表明，可以通过建立提升系统动力学方程分析卷筒制造误差[6-7]和钢丝绳圈间过渡[8-9]对钢丝绳张力差的影响。龚宪生等[3]通过有限元法计算了卷筒同右出绳方式下的绳长差，但未考虑绳长差与卷筒变形的相互影响。罗宇驰[10]在求解卷筒变形时，将两钢丝绳长度差对其张力差的影响分开计算，模型不够完善。宁显国等[11]分析了出绳方式对提升机主轴受力的影响规律。刘文强等[12]分析了钢丝绳缠绕变形下的绳槽参数变化规律。WU Juan[13]建立了钢丝绳受拉伸载荷时的有限元模型。王刚等[14]采用有限元的方法以降低卷筒质量与支轮应力为指标对支轮位置进行了优化。WU Juan等[15]通过建立提升系统横纵耦合模型，得出了钢丝绳的横向振动特性。YU Zhenliang等[16]利用有限元方法分析了卷筒的应力应变。JIN Minjie等[17]根据弹性基础梁理论求解了卷筒的变形。刘守成等[18]研究了多层缠绕卷筒径向压力，并提出了计算多层缠绕系数的方法。葛世荣等[19]考虑了绳圈与卷筒之间的相互作用，对钢丝绳缠绕过程中卷筒的受力进行详细的理论分析。

笔者针对现有研究的不足，将考虑钢丝绳长度、钢丝绳张力以及卷筒变形3者间的相互影响，建立相应的力学模型和数学模型，并求解提升过程中不同出绳方式和不同支轮布置位置下钢丝绳最大张力，以此探讨卷筒结构对钢丝绳张力差的影响规律，为超深矿井提升机卷筒的设计及系统运行安全提供理论参考。

1 钢丝绳张力

双绳多层缠绕式提升结构如图1所示，其卷筒结构如图2所示，卷筒采用厚壳弹支结构，有左右2个缠绳区，每个缠绳区可有左或右2个出绳孔和1个支轮，钢丝绳从不同的出绳孔出绳以及支轮的不同位置布置会直接影响两缠绳区在钢丝绳缠绕过程中的变形同步性。

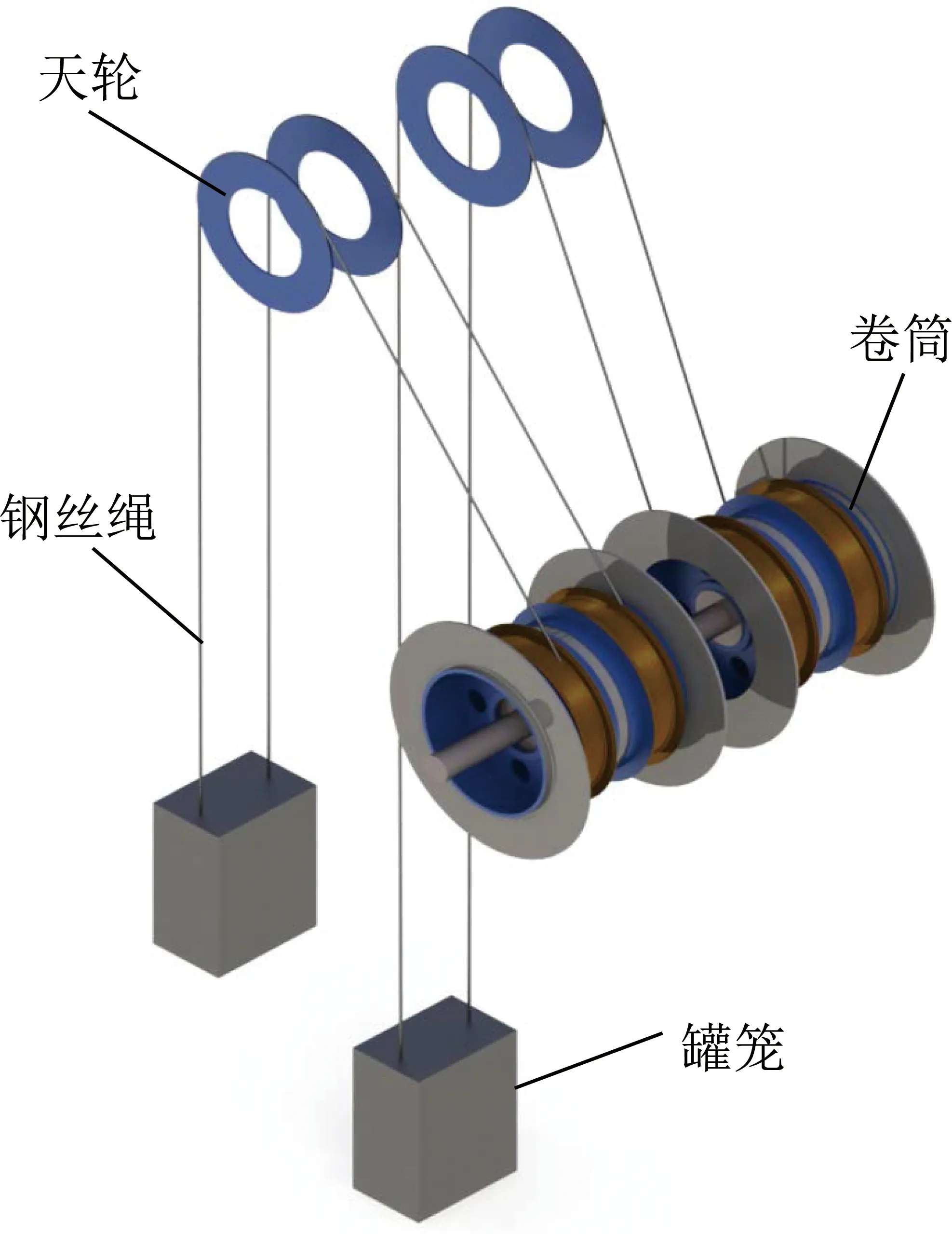
图1 双绳多层缠绕式提升机Fig.1 Double-rope multi-layer winding hoist

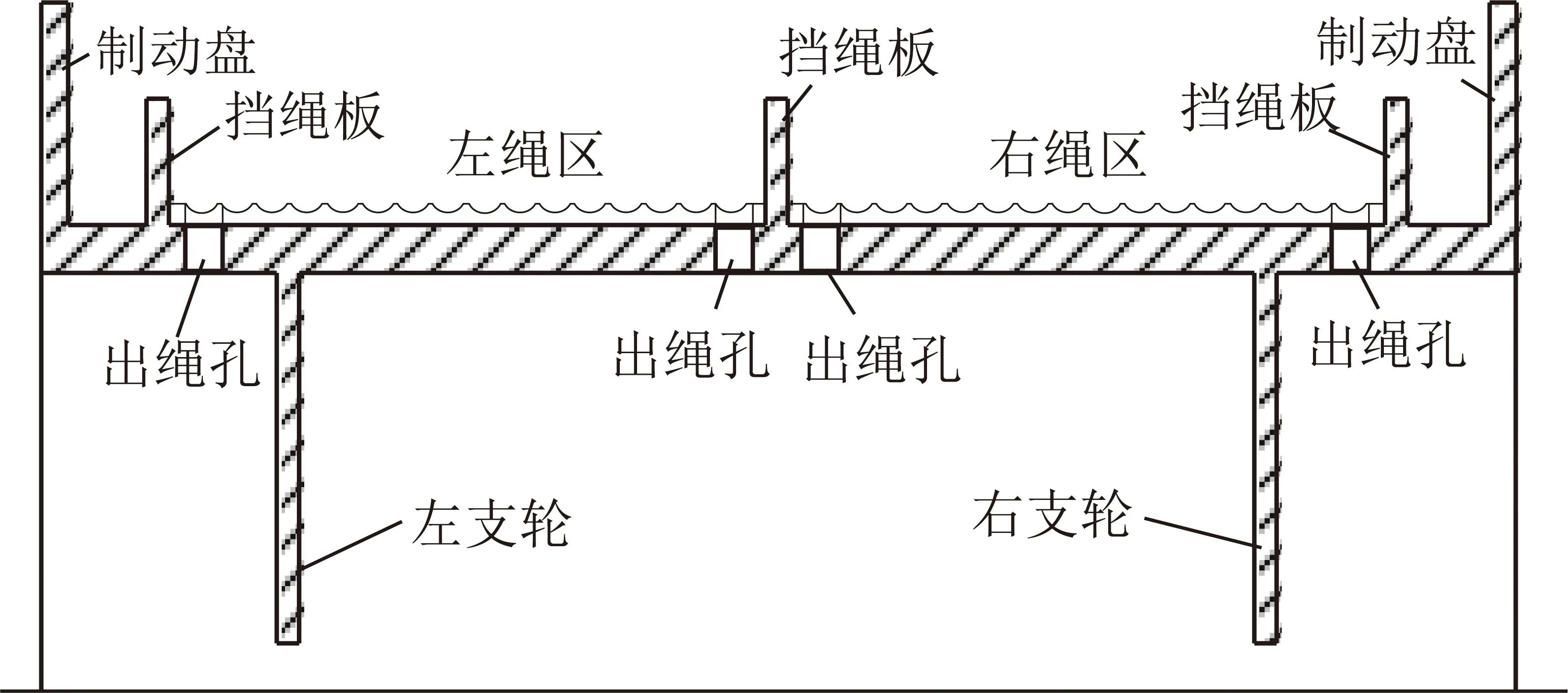
图2 双绳多层缠绕式提升机卷筒结构示意Fig.2 Drum structure of double-rope multi-layer winding hoist

由于缠绕绳圈的节距相对卷筒直径来说很小，为了简化计算可以把缠绕在卷筒上的绳圈视为封闭圆环，在每一圈的范围内压力均布。钢丝绳以一定张力每缠绕完成一圈后，钢丝绳张力会因提升高度、提升速度、提升加速度的变化而产生变化，提升系统将缠绕第n圈时两钢丝绳的总张力Tn为

Tn=S0-4(n-1)πRpg+(K-1)Qg/2+

[S0/g-4(n-1)πRp+2lsp+Wt]an-1

(1)

式中，S0为系统最大静张力，N;R为卷筒半径，m;p为钢丝绳单位质量，kg/m;K为罐道提升阻力系数;Q为一次提升量，kg;g为重力加速度,m/s2;ls为悬绳长度，m;Wt为天轮变位质量，kg;an-1为缠绕n-1圈后的提升加速度，m/s2。

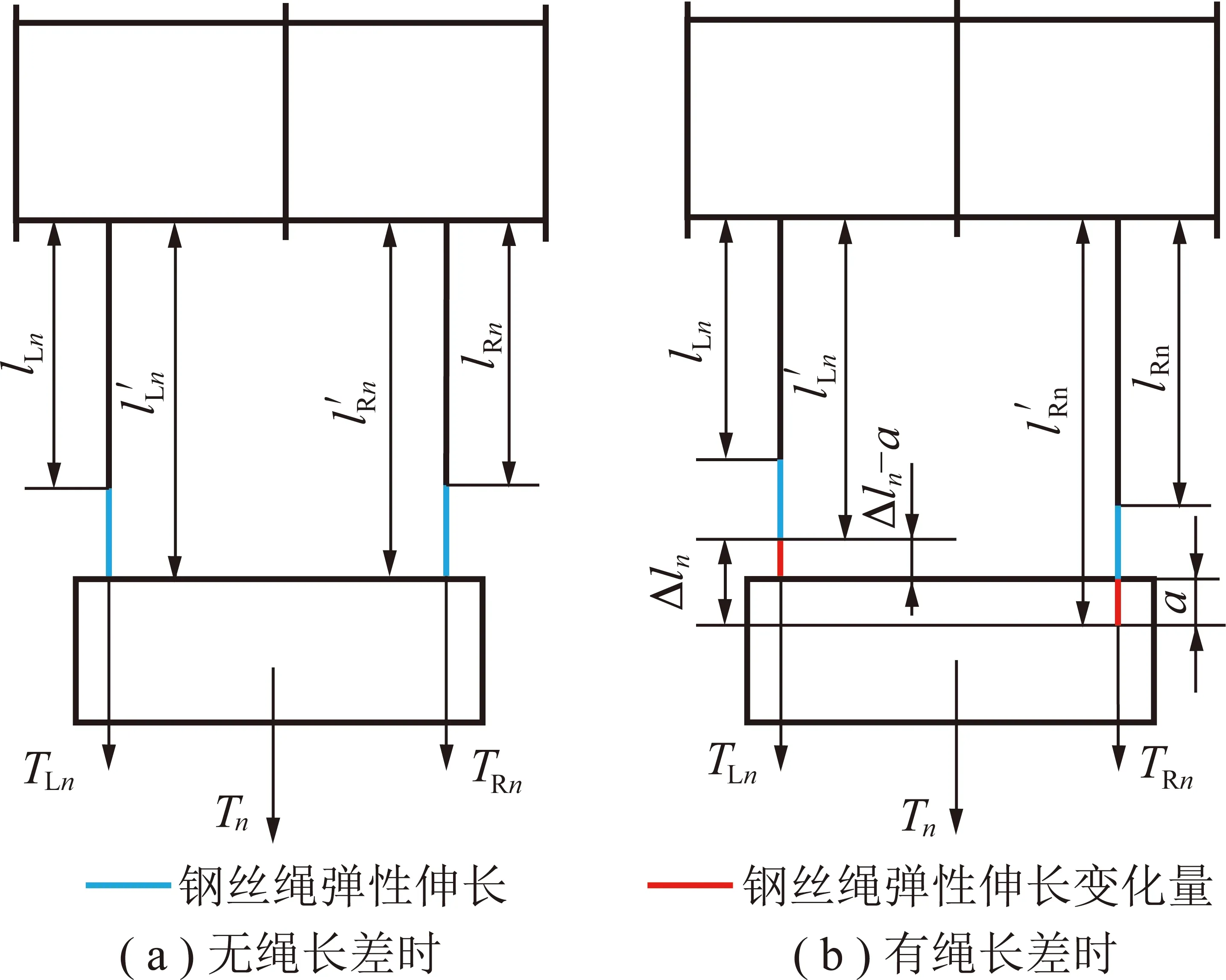
图3 钢丝绳长度差分析模型Fig.3 Wire ropes’ length difference analysis model

第n-1圈缠绕完成后，令一根钢丝绳张力占两钢丝绳总张力的比例系数为bn-1，则另一根钢丝绳的比例系数为1-bn-1。那么第n圈缠绕时，两钢丝绳的张力分配为上一圈缠绕完成后的相应比例系数bn-1和bn-1。

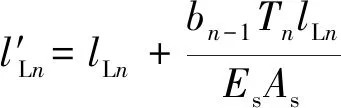
(2)

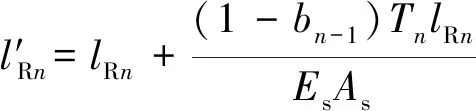
(3)

式中，Es为钢丝绳纵向弹性模量，Pa;As为钢丝绳断面钢丝面积总和，m2。可得两绳原始长度为

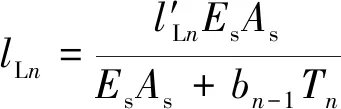
(4)

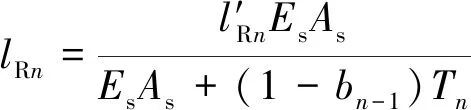
(5)

绳长差Δl为

Δl=l′Rn-l′Ln

(6)

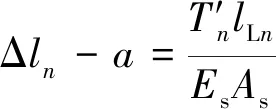
(7)

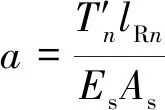
(8)

联立式(2)～(8)可得张力变化量

(9)

那么最终的比例系数为

(10)

随着钢丝绳连续缠绕，后续绳圈会对已缠绕绳圈处产生变形增量，从而使得已缠绕绳圈出现拉力降低现象。对于一层缠绕，钢丝绳缠绕至n圈时，第j圈已缠绕绳圈的拉力降低量ΔPj为

(11)

式中，yjn为缠绕至第n圈时卷筒第j圈处的变形量，m-1。

对于多层缠绕，由于第m层第n圈的缠绕，引起筒壳径向增量和i层以下各层以及i层的压缩，造成第i层钢丝绳缠绕半径减小，进而引起第i层钢丝绳张力的减小，其降低量Pi·m[20]为

[λ0(Pm·n′-P1·m-P2·m-…-P(m-1)·m)+

λ1(Pm·n′-P2·m-P3·m-…-P(m-1)·m)+…+

λi-1(Pm·n′-Pi·m-P(i+1)·m-…-P(m-1)·m)+

λi(Pm·n′-P(i+1)·m-P(i+2)·m-…-P(m-1)·m)/2]

(12)

式中，i=1,2,…,n-1;λ0=R/(t0δEd);λ1=(1+sinα)×[2-νrcot(α+γ)]/[2Er(2R+d)];λi=2sinα[1-νrcot(α+γ)]/Er{2R+[1+2(i-1)sinα]d}(i≠1);Pi·m为m层缠绕时引起第i层钢丝绳拉力降低量，N;Pm·n′为第m层第n′圈缠绕时第i层钢丝绳的拉力，N;νr为钢丝绳泊松比;Er为钢丝绳横向弹性模量，Pa;d为钢丝绳直径，m;t0为钢丝绳缠绕节距，m;μr为绳间摩擦因数;γ=arctanμr;α为钢丝绳堆叠角，(°)。

2 卷筒变形

左右钢丝绳每缠绕一圈时，卷筒受到的力由3部分组成:由左右钢丝绳缠绕绳圈产生的压力，由左右支轮相应产生的支反力和支反力偶。其中支反力偶对卷筒变形的影响很小，可以忽略不计[21]。

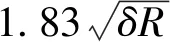
如图4(a)所示，以长度为L的弹性基础梁左端为原点建立直角坐标系，当集中力与梁两端的距离均大于d时为无限长梁计算模型，卷筒的径向变形方程为

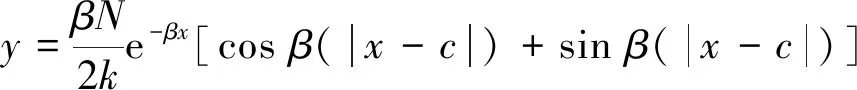
(13)

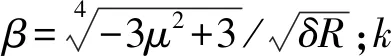
为了方便书写，定义

(14)

如图4(b)所示，当集中力N与梁的左端距离小于d，与右端距离大于d时为左半无限长梁计算模型，卷筒的径向变形方程为

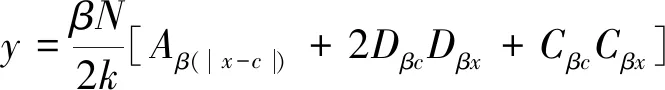
(15)

如图4(c)所示，当作用力N与梁的右端距离小于d，与左端距离大于d时为右半无限长梁计算模型，卷筒的径向变形方程为

(16)

图4 不同类型弹性基础梁受力模型Fig.4 Different types of elastic foundation beams

当作用力N与两端距离均小于d时为有限长弹性基础梁计算模型，而双绳缠绕式提升机卷筒的长度L远大于d，故不存在该种情况下的计算。

卷筒的受力分析模型如图5所示，当左、右钢丝绳缠绕第n绳圈时，可根据其对应的缠绕位置xLn，xRn判定计算模型，代入对应缠绕压力NLn，NRn就可求解出左、右缠绕绳圈相应产生的卷筒径向变形yLn和yRn。同理，根据左、右支轮的位置xsL，xsR和支反力NsLn，NsRn，可以求解出左右支轮相应产生的变形ysLn和ysRn。那么第n圈对卷筒产生的整体变形方程为

yn=yLn+yRn+ysLn+ysRn

(17)

支轮受到径向压力N0产生变形ys，N0与支反力大小相等，方向相反。由于支轮的人孔尺寸相对于支轮尺寸较小，且本文主要关注支轮位置不同所产生的影响，为简化计算，将支轮视为弹性圆板支轮，根据支轮受压变形ys公式[23]为

(18)

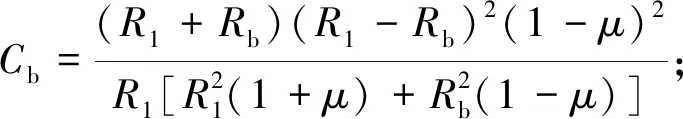
图5 卷筒受力模型Fig.5 Force analysis model of the drum

结合变形协调条件:在支轮处(R1=R)，支轮径向变形与卷筒径向变形相等，可以分别建立在左、右支轮处的等式

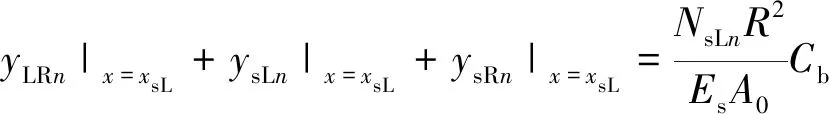
(19)

(20)

其中，yLRn=yLn+yRn。联立式(19)，(20)，再根据左、右支轮所处位置的不同，可以求得缠绕至第n圈时左右支轮支反力的大小。为了方便书写表达，定义

k1=-βAβ(xsR-xsL)/2k

k2=-β/2k-CbR2/EsA0

k3=-β(Aβ(xsR-xsL)+2Dβ(L-xsR)Dβ(L-xsL)+

Cβ(L-xsR)Cβ(L-xsL))/2k

k4=-β(Aβ(xsR-xsL)+2DβxsLDβxsR+CβxsLCβxsR)/2k

k5=-β(1+2Dβ(L-xsR)Dβ(L-xsR)+Cβ(L-xsR)Cβ(L-xsR))/

2k-CbR2/EsA0

k6=-β(1+2DβxsLDβxsL+CβxsLCβxsL)/2k-

CbR2/EsA0

(21)

当xsL≥d且L-xsR≥d时，即左、右支轮皆为无限长梁计算模型:

NsLn=(k2yLRn|x=xsL-k1yLRn|x=xsR)/(k1k1-k2k2)

(22)

NsRn=(-k1yLRn|x=xsL+k2yLRn|x=xsR)/(k1k1-k2k2)

(23)

当xsL≥d且L-xsR

NsLn=(k5yLRn|x=xsL-k3yLRn|x=xsR)/(k1k3-k2k5)

(24)

NsRn=(-k4yLRn|x=xsL+k6yLRn|x=xsR)/(k1k4-k2k6)

(25)

当xsL

NsLn=(k2yLRn|x=xsL-k1yLRn|x=xsR)/(k1k4-k2k6)

(26)

NsRn=(-k1yLRn|x=xsL+k2yLRn|x=xsR)/(k1k3-k2k5)

(27)

当xsL

NsLn=(k5yLRn|x=xsL-k3yLRn|x=xsR)/(k3k4-k5k6)

(28)

NsRn=(-k4yLRn|x=xsL+k6yLRn|x=xsR)/(k3k4-k5k6)

(29)

将求得的左、右支轮支反力代入整体变形方程(17)中，即可求得任意支轮位置下，钢丝绳缠绕至第n圈时，卷筒任意位置的径向变形大小，将前n圈的变形进行叠加求和就可求得缠绕至第n圈时卷筒的累计总变形。

3 不同卷筒结构下的钢丝绳张力差

利用MATLAB编写程序，以左右钢丝绳的张力均等于系统最大静张力的1/2作为初始条件，求解卷筒在缠绕1圈后产生的径向变形，并考虑钢丝绳张力降低量以及卷筒变形差异所造成的两钢丝绳张力差，得到1圈缠绕完成后两钢丝绳新的张力值，进而求解下1圈的卷筒变形及钢丝绳张力。对提升机在卷筒不同出绳方式、不同支轮布置位置下进行提升全过程计算，求解缠绕过程中出现的钢丝绳最大张力差。

3.1 工况与参数

以中信2JKD-8×4.2双绳缠绕式矿井提升机参数进行计算:提升高度为1 500 m，卷筒直径8 m，缠绳区宽度2.1 m，钢丝绳直径76 mm，绳槽节距78 mm，钢丝绳单位质量23.4 kg/m，系统最大静张力480 kN，有效提升载荷30 t，罐笼自重50 t，共缠绕3层，第1，2层各缠26圈，含3圈摩擦圈，第3层约10圈，最大提升速度18 m/s，加减速度均为0.75 m/s2，按加速、匀速和减速3个阶段运行。

为方便后文叙述，首先定义左支轮与左缠绳区出绳孔的距离为“左轮孔距离”，右支轮与右缠绳区出绳孔的距离为“右轮孔距离”。如图6所示，由卷筒出绳方式的不同分为4种工况，为避免出绳孔被遮挡，出绳孔对应绳槽处不布置支轮，故将左右支轮布置于每种工况下除出绳孔对应绳槽以外的25个绳槽对应位置，以左轮孔距离或右轮孔距离为多少个绳槽节距进行编号，左缠绳区的支轮位置编号为L1，L2，…，L25，右缠绳区的支轮位置编号为R1，R2，…，R25。

图6 工况Fig.6 Working conditions

3.2 结果与分析

图7(a)，(c)，(e)，(g)为4种工况下钢丝绳最大张力差，可以看出:4种工况均存在张力差超过10%甚至高达20%的情况;4种工况均存在张力差低于2%(最优布置位置)与低于4%(次优布置位置)的2种支轮布置规律;工况1(左右出绳)与工况2(右左出绳)之间的最大张力差分布规律相同，这是因为这2种出绳方式均具有结构上的对称性，于相同轮孔距离下的两缠绳区缠绕变形同步性情况相同;工况3(同左出绳)与工况4(同右出绳)之间最大张力差分布规律呈对角线对称关系，这是因为这两种出绳方式之间存在对称关系，两出绳方式各自的支轮布置位置互为对称时的两缠绳区缠绕变形同步性相同。

图7(b)，(d)，(f)，(h)为提取出的每种工况下最优与次优支轮布置位置，可以看出:工况1与工况2下的支轮最优布置位置均为左轮孔距与右轮孔距相等时的组合，即左右支轮与卷筒对称布置时为最优。左轮孔距离与右轮孔距离之和等于17个绳槽节距时为次优布置位置。工况3中，在右轮孔距离≤R20时:左轮孔距离比右轮孔距离始终多一个绳槽节距、右轮孔距离>R20时:左轮孔距离始终为L21的支轮布置位置为最优。工况4的支轮最优布置位置与工况3沿对角线呈对称分布。工况3与工况4下的左轮孔距离与右轮孔距离之和等于25个绳槽节距时均为次优布置位置。

表1为4种工况下的支轮最优布置位置的张力差范围，可以看出:工况1与工况2之间、工况3与工况4之间在支轮最优布置位置时的张力差范围近似;工况1和工况2在支轮最优布置位置时的张力差范围明显小于工况3和工况4在支轮最优布置位置时的张力差范围。

4 有限元分析

为验证卷筒受力产生变形的计算正确性，将数值分析时得到的4种工况下钢丝绳张力差最低的卷筒结构(右左出绳方式，左、右轮孔距均为4个绳槽节距，如图8所示，缠绕过程中钢丝绳最大张力差0.002%)进行三维建模，并导入Workbench中使用Static Structural模块进行有限元分析。材料定义为Q345，弹性模量206 GPa，泊松比0.3，采用自动划分网格方法，尺寸大小为100 mm，节点数447 379，单元数49 289，在两支轮内径面添加Cylindrical Support约束。如图9所示，将卷筒两缠绳区以绳槽节距进行切割，对每一圈添加周向压力模拟钢丝绳对卷筒的缠绕，设定求解步数为59，模拟钢丝绳对卷筒的59圈缠绕。有限元计算结果如图10所示，卷筒最大变形为2.240 4 mm，两缠绳区变形量呈对称规律。

图7 不同工况下的求解结果Fig.7 Solution results under different working conditions

表1 不同工况下支轮最优布置位置的张力差范围Table 1 Wire ropes’ tension difference range of optimal positions of supporting wheels under different working conditions

图8 张力差最低卷筒结构下的钢丝绳张力变化曲线Fig.8 Wire ropes’ tension difference curve under the optimal drum structure

图9 有限元模型载荷的施加Fig.9 Load of finite element model

图10 有限元计算结果Fig.10 Finite element calculation result

如图11所示，将理论计算与有限元计算下每一圈缠绕时卷筒的最大变形量进行对比，两者的相对误差均不超过10%，验证了理论模型的正确性。

图11 理论计算与有限元计算结果对比Fig.11 Comparison of theoretical calculation and finite element calculation

5 结 论

(1)提升机卷筒结构对双绳多层缠绕钢丝绳提升同步性具有重要影响，卷筒出绳方式与支轮位置的不合理组合会导致钢丝绳间张力差超过10%，危及提升系统的运行安全。

(2)可采用左、右轮孔距离之间的关系对不同卷筒结构下两钢丝绳缠绕同步性进行规律总结。

(3)卷筒左右与右左出绳方式下的两钢丝绳缠绕同步性在左、右轮孔距离分别相等时是相同的;卷筒同左与同右出绳方式下的两钢丝绳缠绕同步性在左、右支轮布置位置互为对称时是相同的。

(4)卷筒左右或右左出绳方式下，支轮对称布置时，缠绕过程中的两钢丝绳张力差最小。

(5)研究方法及成果可对超深矿井双绳多层缠绕式提升机的卷筒结构设计和两钢丝绳之间的缠绕同步性保证提供理论参考。