基于时频熵特征的2.25Cr-1Mo损伤开裂声发射识别方法研究*
邱 枫,白永忠,单广斌,屈定荣,李明骏
(中国石化青岛安全工程研究院,山东青岛 266104)
0 前言
加氢反应器是现代石油化工行业的典型设备,该设备的特点是处于高温、高压和临氢环境,目前国内加氢反应器采用的结构为板焊式和锻焊式[1],2.25Cr-1Mo是加氢反应器的常用材料之一。基于其加氢反应器运行环境和损伤机理,焊缝形成应力腐蚀裂纹是其主要的损伤问题。一旦裂纹发生开裂,将造成严重的安全事故,因此,对加氢反应器进行损伤裂纹扩展在线监测具有十分重要的意义[2]。声发射作为一种无需停产、在线监测裂纹活性的技术手段,可以作为加氢反应器的安全运行监测方法,而损伤裂纹扩展的声发射信号的有效识别是加氢反应器声发射在线监测技术的关键。
时频分布是时间和频率的联合分布函数,有利于提取信号的局部特征,是非平稳信号分析的有效方法。HHT(Hilbert-Huang Transform)是先对信号进行经验模态分解,得出本征模态函数,再对本征模态函数进行希尔伯特变换,从而进一步得到该信号的希尔伯特谱、时频能量谱等,对非线性及非平稳信号有较好的分析和处理效果[3]。
裂纹扩展声发射信号具有时域、频域的特征,但是现场监测时仅仅从时域、频域进行特征提取并不能将有效信号与噪声信号区分。裂纹扩展声发射信号具有随机性并具有复杂多样性,而背景噪声、电磁干扰信号往往具有一定的周期性和重复性,信息熵可以描述信号的复杂性,因此将其引入用于表征损伤裂纹扩展信号。信号的时频分布是描述信号在采样时间内各个频率处的能量变化,裂纹扩展时的时频分布往往发生变化,采用信息熵理论结合时频分布可以定量描述这种变化程度。在识别方面,支持向量机(Support Vector Machine, SVM)是建立在统计学习理论VC维(Vapnik-Chervonenkis dimension, VC dimension)和结构风险最小化原理基础上的机器学习方法,在解决小样本、非线性和高维模式识别问题中表现出特有优势[4],可以用于对损伤扩展监测试验声发射信号的分类识别。
本文开展基于时频熵特征的2.25Cr-1Mo损伤开裂声发射识别方法研究,采用三点弯曲试验进行试样损伤受力情况模拟,采集监测过程的声发射信号,基于HHT提取声发射信号的时频熵特征,以支持向量机构造识别模型,实现对2.25Cr-1Mo材料损伤开裂过程声发射信号的有效识别,为现场加氢反应器等压力容器损伤开裂声发射在线监测评价提供依据。
1 2.25Cr-1Mo材料三点弯曲声发射监测试验
试件采用加氢反应器常用材料2.25Cr-1Mo,材料化学成分和机械性能见表1。实验装置由试件、WD传感器、2/4/6前置放大器、PCI-2全数字声发射仪等,SANS万能电子拉伸机组成。监测试验系统中装置连接见图1,传感器布置如图2。

表1 2.25Cr-1Mo化学成分和机械性能
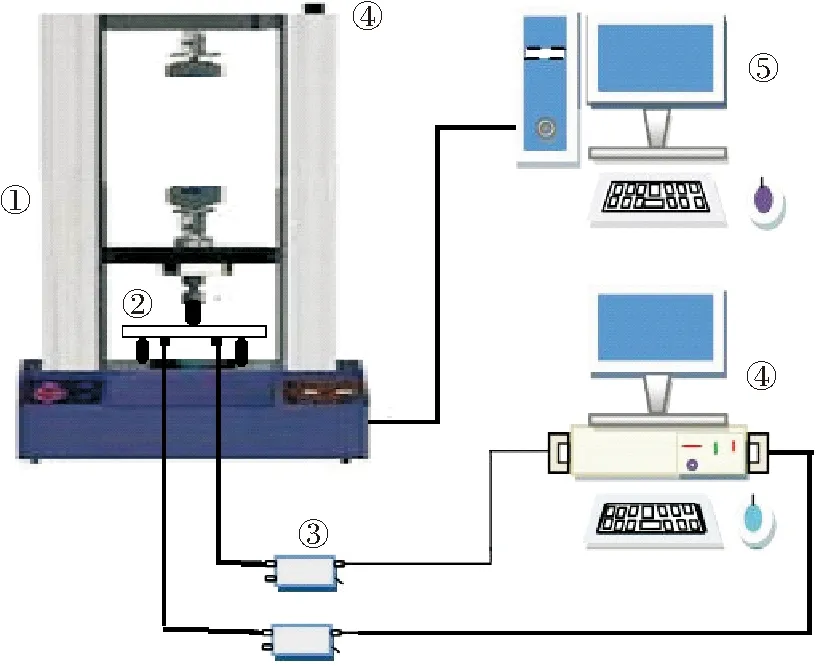
图1 三点弯曲声发射监测试验装置

图2 传感器布置
将传感器固定在试件上,再将试件放置在材料试验机上,并在支点和压头处放橡胶垫,然后对声发射检测系统的灵敏度进行校准。材料试验机具体加载过程:①利用材料试验机以10 N/s的速度缓慢加载至3 kN,并保持载荷5 min;②以10 N/s的速度缓慢卸载到0.1 kN,并在当前载荷下保载5 min;③重复第①和第②步2次;④将力控制改为位移控制,以0.1 mm/min的速度缓慢加载至试件产生明显塑性变形。
采集整个加载过程的声发射信号。2.25Cr-1Mo试件的加载载荷曲线及声发射信号幅值历程见图3、图4。对比两图可以发现在前3次加载过程中,声发射撞击数逐渐减少:第1次加载阶段撞击数最多且最高幅值达到67 dB,这主要是由于压头、支架、橡胶垫片和试件初次接触时表面不平造成的,为噪声信号;第2次加载阶段信号明显减少,仅出现5个信号;第3次加载阶段没有信号产生。这一现象符合声发射理论中的Kaiser效应,即重复载荷到达先前所加最大载荷以前不发生明显声发射。
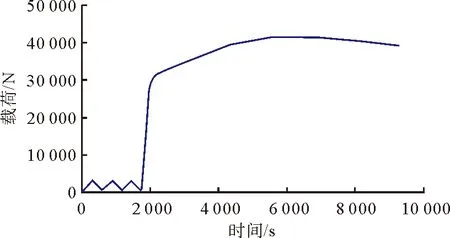
图3 试件加载过程载荷-时间曲线
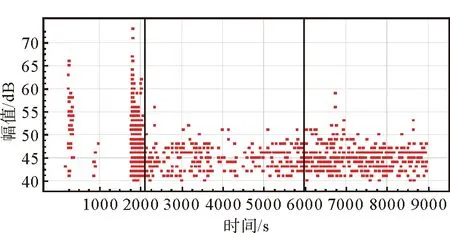
图4 声发射信号幅值历程
2 2.25Cr-1Mo材料损伤开裂声发射信号识别
2.1 基于Hilbert-Huang变换的时频熵
不同信号在时频分布上的差异表现为时频平面上不同的小块时频段的能量分布的差异,各时频区能量分布的均匀性则反映了损伤状态的差别,信息熵是概率分布均匀程度的度量。若P(p1,p2,…,pn)是一个不确定的概率分布,k为任意常数,那么这个分布的信息熵[5]为:
(1)
由式(1)可知,最不确定的概率分布具有最大的熵值,越接近等概率分布熵值也就越大,换言之,信息熵值反映了概率分布的均匀性,因此可以对系统的不确定程度进行描述。
HHT谱反映了信号的能量随频率和时间变化的情况,不同阶段下试件声发射信号在时频面上的分布也不同,具体表现在时频平面上不同区域所包含的能量大小的差别,每个区域能量分布的均匀性可以反映试件所处阶段的不同,为定量描述这种差异,可将信息熵和HHT谱相结合。将Hilbert谱的时-频平面划分为N个面积相等的时-频块,每块内的能量为W(i)(i=1,2,…,N),整个时-频平面的能量为A,对每块进行能量归一化,得到qi=Wi/A,仿照信息熵的计算公式,基于Hilbert-Huang变换的时频计算公式为:
(2)
2.2 时频熵特性提取
由图3、图4可以明显看出试件在弯曲过程中分为3个阶段,即弹性阶段、塑性阶段和断裂分离阶段。根据这一特点,分别提取该3个阶段的声发射特征参数,基于Hilbert-Huang变换求得时-频平面的能量谱,又因各阶段的HHT谱是不同的,这种差异反映了信号的内在特征,故可以对各阶段声发射信号的HHT谱进行时-频熵分析,提取出信号的特征。根据时频熵的大小,可以判断出声发射信号所处的阶段,以此可以有效地对材料所处的阶段进行识别检测。
在弹性阶段、塑性阶段和断裂分离阶段分别选取10组声发射信号数据作为样本,T1~T10为T样本、S1~S10为S样本,D1~D10为D样本,其各自的特征参数如表2~表4所示。

表2 弹性阶段声信号特征参数
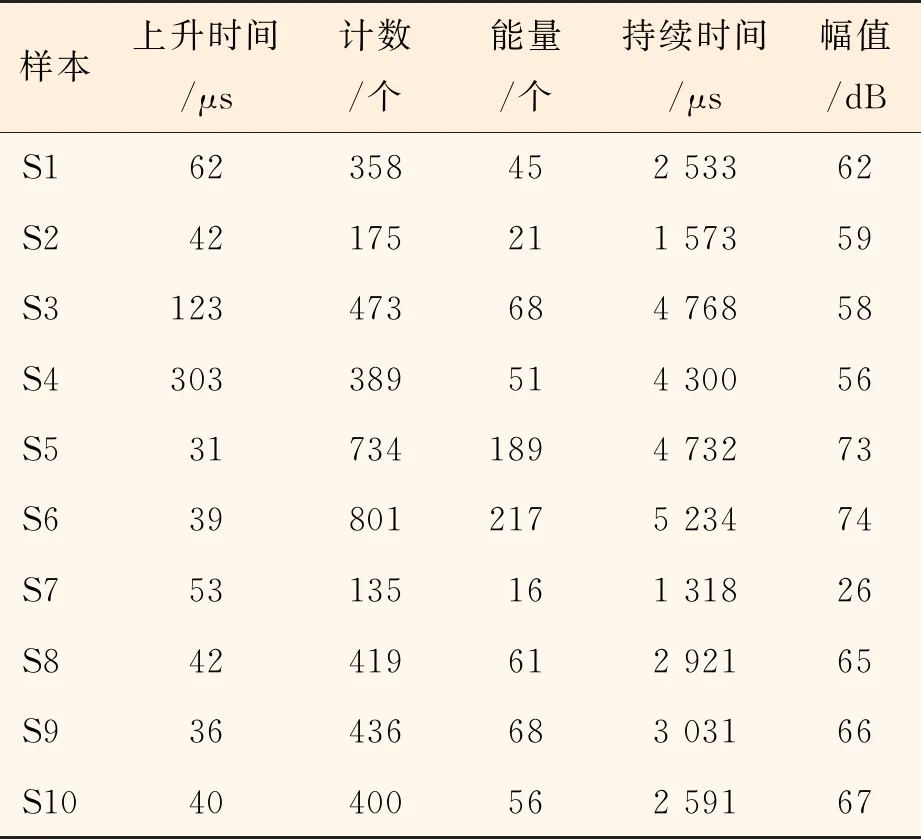
表3 塑性阶段声信号特征参数
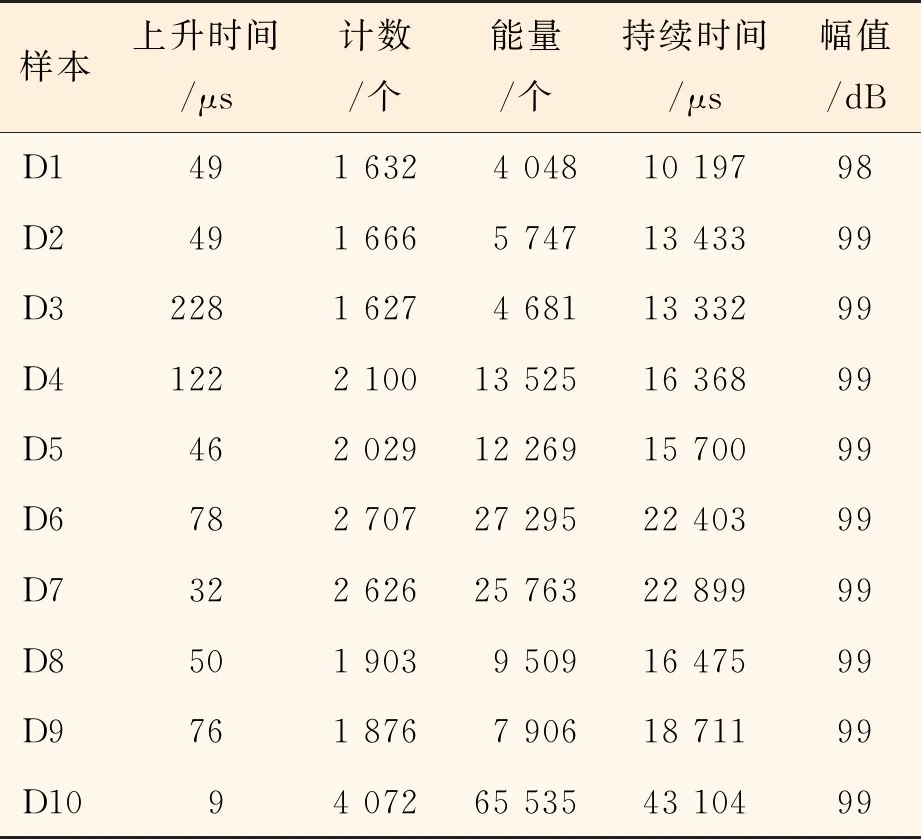
表4 断裂分离阶段声信号特征参数
基于Hilbert-Huang变换,分别提取的三点弯曲试验样本在弹性阶段、塑性阶段和断裂分离阶段的声信号时频熵特征参数,如表5~表7所示。
2.3 识别结果与分析
a) 弹性阶段所采集到的10个样本的时频熵特征集中在6.92~7.19之间,平均值为7.05,均方差为0.097,可见该试件在弹性阶段声发射信号的时频特征的能量分布是较均匀的,这是因为在弹性阶段,金属原子之间随着原子间距的改变,原子间的相互作用力将产生作用,即电荷间的库仑力,在试件受到较小压力时即达到屈服应力之前,原子受力是稳定的,能量分布均匀,仍做无序热运动,故采集到的声发射信号的时频熵的值较大。

表5 弹性阶段声信号的时频熵特征

表6 塑性阶段声信号的时频熵特征

表7 断裂分离阶段声信号的时频熵特征
b) 塑性阶段所采集到的10个样本的时频熵特征集中在6.59~6.84之间,平均值为6.72,均方差为0.084,可见该试件在塑性阶段声发射信号时频特征的分布发生了不均匀的变化,这是因为在塑性阶段,受到了更大应力,金属材料晶体在外力作用下发生一致性的改变,在晶轴方向的应力破坏了金属原子间的金属键,受到破坏的金属原子与相邻的原子结合成新的金属键,晶格结构发生了不可逆转的永久变形,这时,材料内部不断发生错位滑移,出现多个位错堆积,材料间原子之间的稳定状态被破坏,能量分布不均匀,故采集到的声发射信号的时频熵的值比较小。
c) 断裂分离阶段所采集到的10个样本的时频熵特征集中在6.87~7.28之间,平均值为7.04,均方差为0.116,可见该试件在断裂分离阶段声发射信号视频特征的能量分布又向均匀转变,因为在断裂分离阶段前期,金属内部位错已积累到很高的程度,这时的位错塞积很严重,金属晶体所受到的外力破坏之间的金属键,从而晶体之间出现裂缝,随着外力的增加发生断裂分离,裂缝自由扩展,直到试件完全断裂,此时,金属材料原子突破束缚、向稳定状态改变,故采集到的声发射信号的时频熵的值比较大。
采用SVM对不同阶段声发射信号提取的时频熵特征进行识别。为了保证分类器具有较好的推广能力,采用交叉验证法,5折样本训练法,即把样本分成5份,在每份上训练,在其他份上测试。识别结果如图5所示:识别精度为96.7%,30个样本中只有1个识别错误,第2类1个样本被识别为第1类。表明采用时频熵作为声发射信号特征向量,以支持向量机作为识别分类器的损伤开裂识别方法具有较高的准确度。

图5 SVM识别结果
3 结论
a) 提出了基于HHT时频熵的声发射识别方法,该方法将声发射信号进行HHT变换,求取信号的时频熵,通过对比时频熵的大小来判断试件所处的阶段。
b) 基于HHT的时频熵变换,获得试样在各阶段的时频熵特征,可知该试件在经历弹性阶段-塑性阶段-断裂分离的过程中,声发射信号的时频能量分布是由大变小再转为大。
c) 在时频特征的基础上,加入熵的特征提取方法,即使是小样本,也达到了较好的识别效果。

