偏最小二乘模型在黄土坡面土壤侵蚀中的应用研究

金 鑫，李 霞，宋 颖，王春振，赵华荣

(1.桂林理工大学广西环境污染控制理论与技术重点实验室，广西 桂林 541004；2.桂林理工大学岩溶地区水污染控制与用水安全保障协同创新中心，广西 桂林 541004)

0 引 言

土壤侵蚀是多种因素共同作用的复杂过程，降雨强度、坡度、降雨历时、土壤初始含水率、抗剪切力作为其中的重要影响因素而得到研究者的广泛关注。已有的研究表明：坡度和降雨强度均为坡面侵蚀的主要影响因子，随着坡度和雨强增加，径流率和产沙量也增加，雨强是径流率变化的主要因素，坡度对产沙量变化的影响较为显著，且存在临界坡度，产流和产沙随降雨历时先迅速增加后趋于稳定[1-4]；初始含水率越高，产流越快，达到稳定入渗率的时间也越短[5]；与坡度、土壤含水率相比，土壤剪切力对侵蚀量影响最小，但其能够显著提高土壤侵蚀量预测精度[6]。

在雨强、坡度、降雨历时、初始含水率、剪切力等因素对土壤侵蚀影响方面已经不少学者分别做了研究，但很少细化这些因素对侵蚀作用的程度。在实际侵蚀过程中，这些因素同时作用于侵蚀过程，其对侵蚀的贡献大小以及与侵蚀产沙的关系需要进行量化，以准确地反映各因素对侵蚀过程的影响程度。

偏最小二乘回归(PLS)是一种新的多元统计数据分析方法，将多元线性回归、典型相关分析和主成分分析进行有机结合，可避免自变量、因变量之间存在的多重线性关系，具有更大的优势，从而使模型精度、稳健性、实用性都得到提高[7]。并在大尺度的流域径流和土壤侵蚀预测中得到较好的应用[8-11]。本文采用偏最小二乘法对黄土坡面土壤侵蚀进行模拟和预测，细化分析雨强、坡度、初始含水率、剪切力、降雨历时等因素对黄土坡面产流产沙过程的影响程度，以期为认识土壤侵蚀过程和水土流失防治提供数据支持和基础见解。

1 材料和方法

1.1 实验装置与材料

本实验在桂林理工大学降雨实验大厅进行，实验所用土壤为取自陕西岔巴沟流域的表层土。实验采用人工模拟坡面降雨，降雨装置由土槽与人工模拟降雨器2个部分组成。实验土槽为钢质，尺寸长×宽×高为：400 cm×120 cm×80 cm，土槽坡度可以自动调节，变化范围为0～30 °，土槽尾部设有簸箕型集水口，用来收集坡面径流，底部有集水口用以收集坡面下渗径流；人工模拟降雨器为顶喷式全自动不锈钢模拟降雨器，配有旋转下喷式喷头，为带压力垂直下喷式降雨，用扬程为50 m的潜水泵供水，降雨高度为6 m，使得雨滴散落在坡面的速度接近自然雨滴终速，雨强为10～200 mm/h，雨滴直径为0.1～6 mm，雨滴的中值粒径及降雨动能与自然降雨条件较为接近[12]。模拟降雨实验之前测定降雨均匀性，测定结果显示降雨均匀性大于80%。综上所述，实验装置设计合理。

1.2 实验和测量

由于黄土高原降雨分布比较集中，多以暴雨形式出现，且根据调查研究，5°以上，细沟侵蚀较强，并发生浅沟侵蚀，15°以上，细沟、浅沟侵蚀强烈[13]。故本实验设置了50、60、70、80 mm/h四个降雨强度，5°、10°、15°、20°四个坡度，共进行16场降雨实验，每场实验每场降雨时长为15或30 min。每次降雨开始前，测定坡面土壤的初始含水率、土壤剪切力、容重。土壤初始含水率通过TDR水分测定仪测定，土壤剪切力通过三头抗剪仪测定，容重采用环刀法测定，每个参数的测定结果均为多次取样的平均值。

降雨开始后，记录降雨开始时间。坡面产流后，记录产流时间，并根据实际产流及产沙情况每间隔0.5～4 min采一次样，直到降雨结束。用量筒收集径流样品，秒表记录相应的采集时间，记录样品体积并进行称重，通过计算得到各个时段的径流率。

样品含沙量的测量方法采用烘干称重法，具体步骤为：采集的样品静置沉淀24 h以上，抽出上清液，将剩余泥沙样倒入烧杯中，放入105 ℃的烘箱中24 h，冷却后取出称重，通过计算得到各个时段的产沙率。

1.3 PLS建模

PLS的原理可表达[14]为：设有q个因变量{y1，y2，…，yq}和p个自变量{x1，x2，…，xp}，为了研究因变量与自变量的统计关系，观测了n个样本点，由此构成了自变量与因变量的数据表X=(x1，x2，…，xp)n×p和Y=(y1，y2…，yq)n×q，偏最小二乘回归分别在X与Y中提取出成分t1和u1(也就是说，t1是x1，x2，…，xp的线性组合，u1是y1，y2，…，yq的线性组合)，t1和u1应尽可能好地代表数据表X和Y，同时，自变量的成分t1对因变量的成分u1又有很强的解释能力，在第1个成分t1和u1被提取后，偏最小二乘回归分别实施X对t1的回归以及Y对t1的回归，如果回归方程已经达到满意的精度，则算法终止；否则，将利用X被t1解释后的残余信息以及Y被t1解释后的残余信息进行第2轮的成分提取，如此反复，直到能达到一个较满意的精度为止，若最终对X共提取了m个成分t1，t2，…，tm，偏最小二乘回归将通过施行yk(k=1，2，…，q)对t1，t2，…，tm的回归，然后表达成yk关于原变量x1，x2，…，xp的回归方程。

PLS建模过程依次为[15]：

(1)数据标准化处理；目的是使样本点的集合重心与坐标原点重合，先将X经标准化处理后的数据矩阵记为E0=(E01，…，E0p)n×p，再将Y经标准化处理后的数据矩阵记为F0=(F01，…，F0q)n×p；

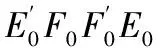
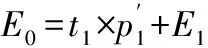
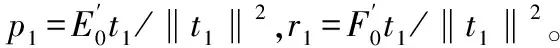
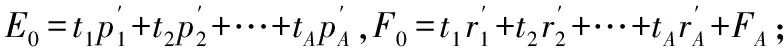
(4)第k成分tk提取；采用步骤(2)及步骤(3)的方法，依次进行推求并对第k成分tk提取，k可用交叉有效性原则进行识别；

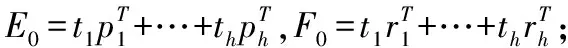
2 结果与分析

2.1 参数选取

通过对影响因素的分析并结合相关研究，将影响坡面径流率(Y1)和产沙率(Y2)的主要因素确定为：坡度(X1)、雨强(X2)、时间(X3)、初始含水率(X4)、剪切力(X5)。选用5°、10°、15°、20°四个坡度，50、60、70、80 mm/h 4个降雨强度在不同的初始含水率、剪切力的16场降雨，其中14场0～30 min降雨过程中的172个径流率、产沙率数据作为建模输入，15°、70 mm/h，20°、80 mm/h的2场降雨在0～15 min的19个径流率、产沙率数据进行检验分析。

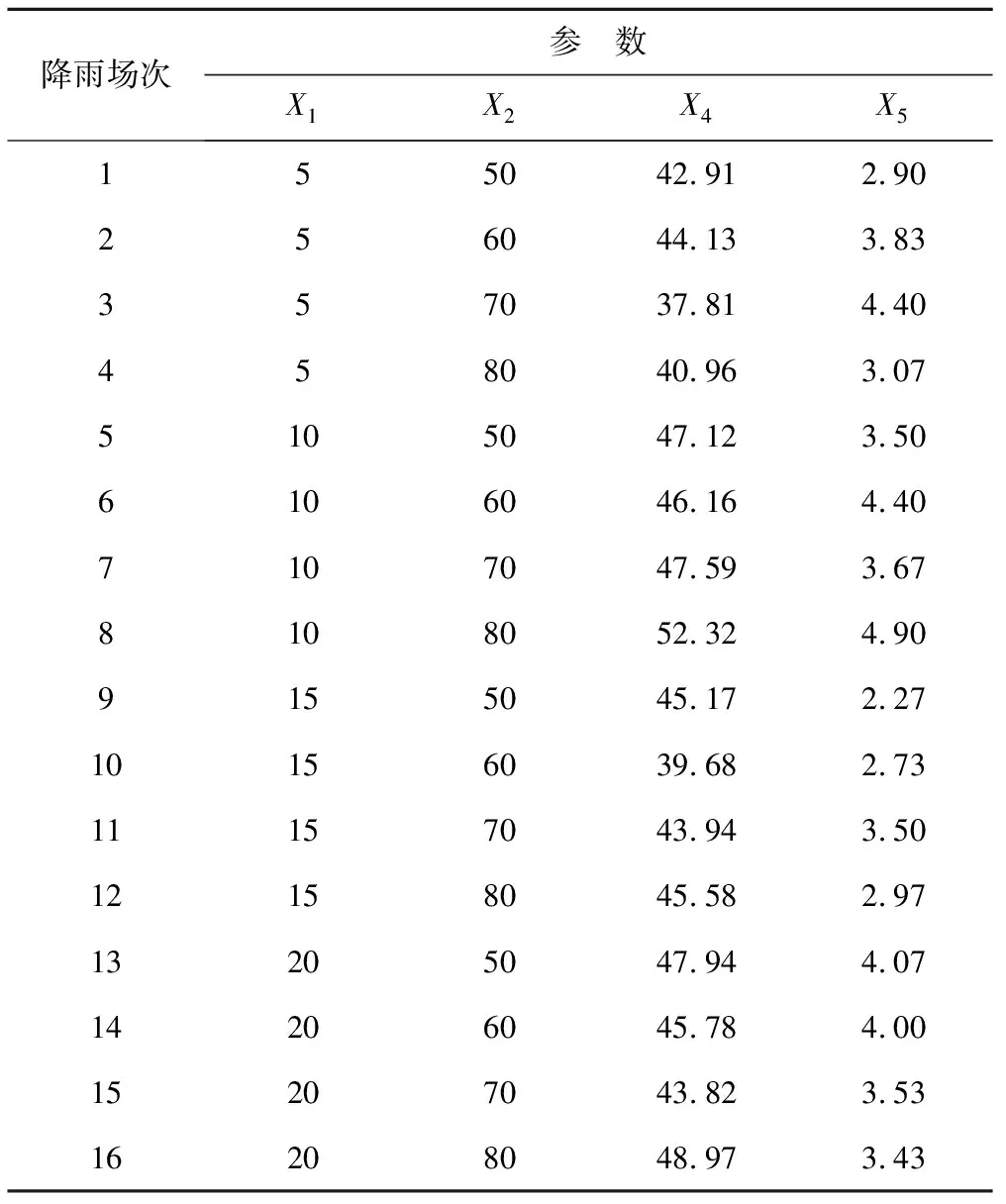
表1 降雨实验影响因素表

2.2 偏最小二乘模型

SIMCA-P是基于主成分分析、偏最小二乘回归分析开发的数据分析软件，因其方便有效的特点，在各个领域获得了广泛应用[7]。本研究通过SIMCA软件构建径流率、产沙率的偏最小二乘模型。

初步假设坡度(X1)、雨强(X2)、时间(X3)、初始含水率(X4)、剪切力(X5)和径流率(Y1)和产沙率(Y2)的关系为线性关系，直接导入数据构建模型。模型的拟合优度R2和预测优度Q2都大于0.6，达到了可以拟合的标准。同时假设坡度(X1)、雨强(X2)、时间(X3)、初始含水率(X4)、剪切力(X5)、径流率(Y1)和产沙率(Y2)的关系为非线性指数叠加关系，通过对数转化重新构建偏最小二乘模型，模型的R2和Q2分别为0.843、0.831，相比较直接线性模拟，指数叠加关系经对数化转变后，模型拟合的效果要更好，故下文采用对数转化后的偏最小二乘模型结果进行论述。

表2为自变量、因变量间的相关系数矩阵。从表2可以看到，自变量间雨强、初始含水率、剪切力之间存在一定的相关性，两个因变量之间的相关性也很强，达到了0.844。偏最小二乘模型可以有效的解决多重共线性问题，同时计算交叉有效性，该模型取3个自变量便达到了满意的精度，则提取3个自变量建模。采用SIMCA软件，通过分析得到的偏最小二乘回归标准化方程为：

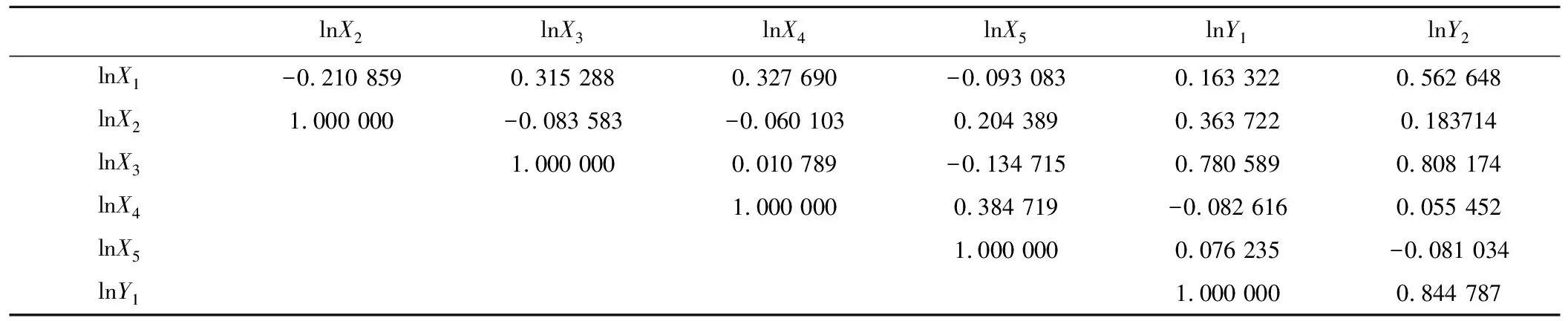
表2 变量之间的相关系数矩阵

lnY1=0.039 493 4×lnX1+0.408 309×lnX2+

0.824 303×lnX3-0.128 515×lnX4+0.145 553×lnX5

lnY2=0.412 347×lnX1+0.341 94×lnX2+

0.706 01×lnX3-0.042 129 9×lnX4-0.023 738 6×lnX5

同时得到了原始的回归方程：

lnY1=0.070 650 6×lnX1+2.014 59×lnX2+

0.810 188×lnX3-1.444 52×lnX4+0.596 852×lnX5-1.167 5

lnY2=1.362 91×lnX1+3.117 17×lnX2+1.282 1×

lnX3-0.874 926×lnX4-0.179 851×lnX5-12.47

即：

变量投影重要性指标VIP，是描述自变量对因变量影响程度的指标，若某个变量的VIP>1，则认为该变量是显著影响因素，值越大说明该自变量对因变量的影响越大[15]。为分析各个自变量对因变量的影响，绘制了变量投影图。如图1所示，采用VIP值来描述每一个自变量对因变量的作用大小。从图1可以看出，VIP的顺序为：X3>X1>X2>X4>X5。根据VIP>1则X在解释因变量时具有重要作用的原则，时间X3(min)、坡度X1(°)解释因变量径流率Y1(mL/s)和产沙率Y2(g/s)时具有重要作用，其中时间X3(min)在解释因变量Y1、Y2时具有最重要的作用。

为了更直观的观测5个自变量对2个因变量的具体作用，针对标准化数据的回归方程，绘制了回归系数图(见图2)。从图2中可以看出，初始含水率对径流率的影响是要高于对产沙率的影响。但无论是对于产沙率还是径流率而言，初始含水率的影响都是负值，初始含水率越高，坡面的径流率和产沙率反而减小，这与文献[5]的研究结果不相一致，这可能是由于各场实验初始含水率本身差值不够明显，开始降雨后极短时间内土壤含水率就趋于饱和，难以避免的实验和观测误差导致模型对影响程度较低的含水率计算不够准确，从而出现随着初始含水率增加，径流率和产沙率总体为减小趋势这一现象。抗剪切力对径流率和产沙率的影响比较有限，对径流率的影响为正值，对产沙率为负值，这表明土壤抗剪切性越强，土壤越不易被侵蚀，坡面比较平整，径流受到的阻碍会越小。

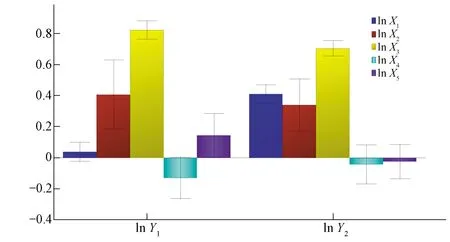
图2 回归系数图

坡度的变化主要是对产沙率产生影响，对于径流率，坡度变化的影响是微乎其微的，这与ZHAO[16]等人的研究结果一致，推测这种情况的出现可能由于在实验的坡度范围存在着临界坡度，使得径流率在这个区间的变化呈现波动，导致模型中无法精确体现出坡度对径流率的影响。降雨强度是径流率变化的一个主要影响因素，这是因为降雨是径流产生的来源，径流率的变化与雨强的变化紧密相关。在降雨初期，由于土壤入渗未达到稳定，径流是逐渐增加的，产沙也相伴增加，二者随降雨历时的变化明显。产沙率的主要影响因素除时间之外，坡度和降雨强度的影响相差较小，受到二者共同作用比较显著，坡度变化，土体的势能和水流动能都发生改变，而降雨强度的变化会使得动能的改变进一步加剧，产生叠加效应，二者交互作用共同影响产沙率的变化。时间对径流率和产沙率变化的影响程度相差不大，径流率和产沙率都随产流后降雨时间的延长而增大。

2.3 精度分析

利用构建的偏最小二乘回归模型，将15°、70 mm/h，20°、80 mm/h的2场降雨在0～15 min的19个径流率、产沙率数据作为输入进行预测检验。通过构建的偏最小二乘方法分别对2场降雨在0～15 min的径流率、产沙率进行预测，分别得到径流率、产沙率的预测值各19个，其中1～10为15°、70 mm/h场次的数据，11～19为20°、80 mm/h场次的数据。图3为实测值与预测值的对比图。

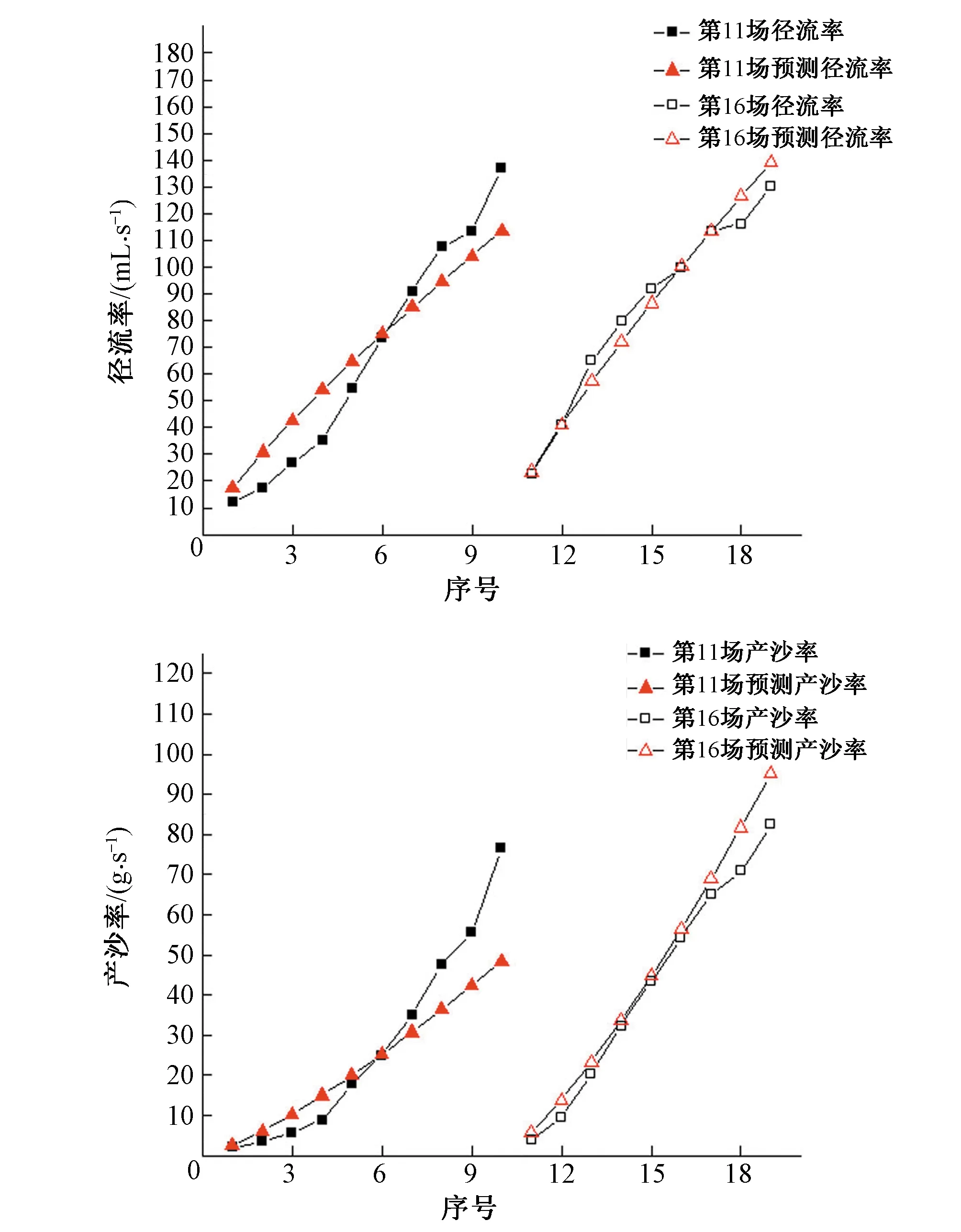
图3 实测值与预测值对比图

平均相对误差绝对值作为评价精度误差分析的一个重要指标[15]，采用该指标进行精度分析。根据平均相对误差绝对值公式：

平均绝对值公式中n为数据个数，y为对应的因变量。将上述2场降雨在0～15 min的19个径流率、产沙率及其预测数据利用上述公式进行计算，得到基于偏小二乘法的平均相对误差绝对值，Y1的平均相对误差绝对值为18.313%，Y2的平均相对误差绝对值为26.698%。同时得到各点的相对误差绝对值，见表3。

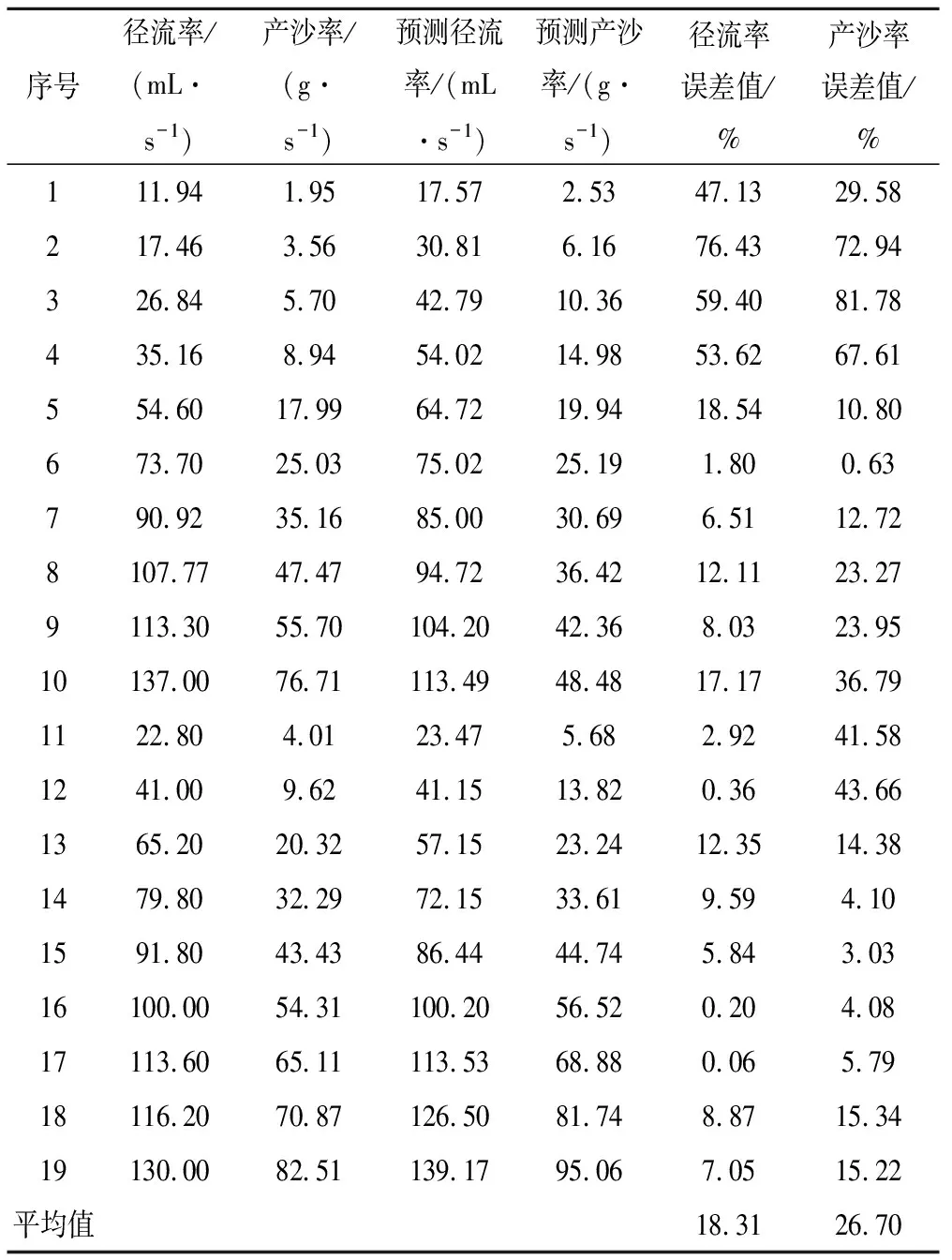
表3 径流率、产沙率误差分析表

从图4中也可以看到，径流率各点实测值与预测值的相对误差绝对值基本要小于产沙率各点实测值与预测值的相对误差绝对值。1～10点的15°、70 mm/h场次无精度分析结果表明偏最小二乘的预测精度较高，可解释性强，能满足实际的需要，特别是相对于产沙率，径流率的预测精度要高得多，模拟预测的效果更好。论是径流率还是产沙率，误差值都较11～19点的20°、80 mm/h场次要大，推测可能是由于在15°附近存在临界坡度，侵蚀变化规律相对复杂，导致预测误差较大。两场实验中前2～3点的误差均要大于后期误差值，可能是由于实验中观测者对产流开始时间判断不一致，初始产流阶段受人为因素影响较大导致。

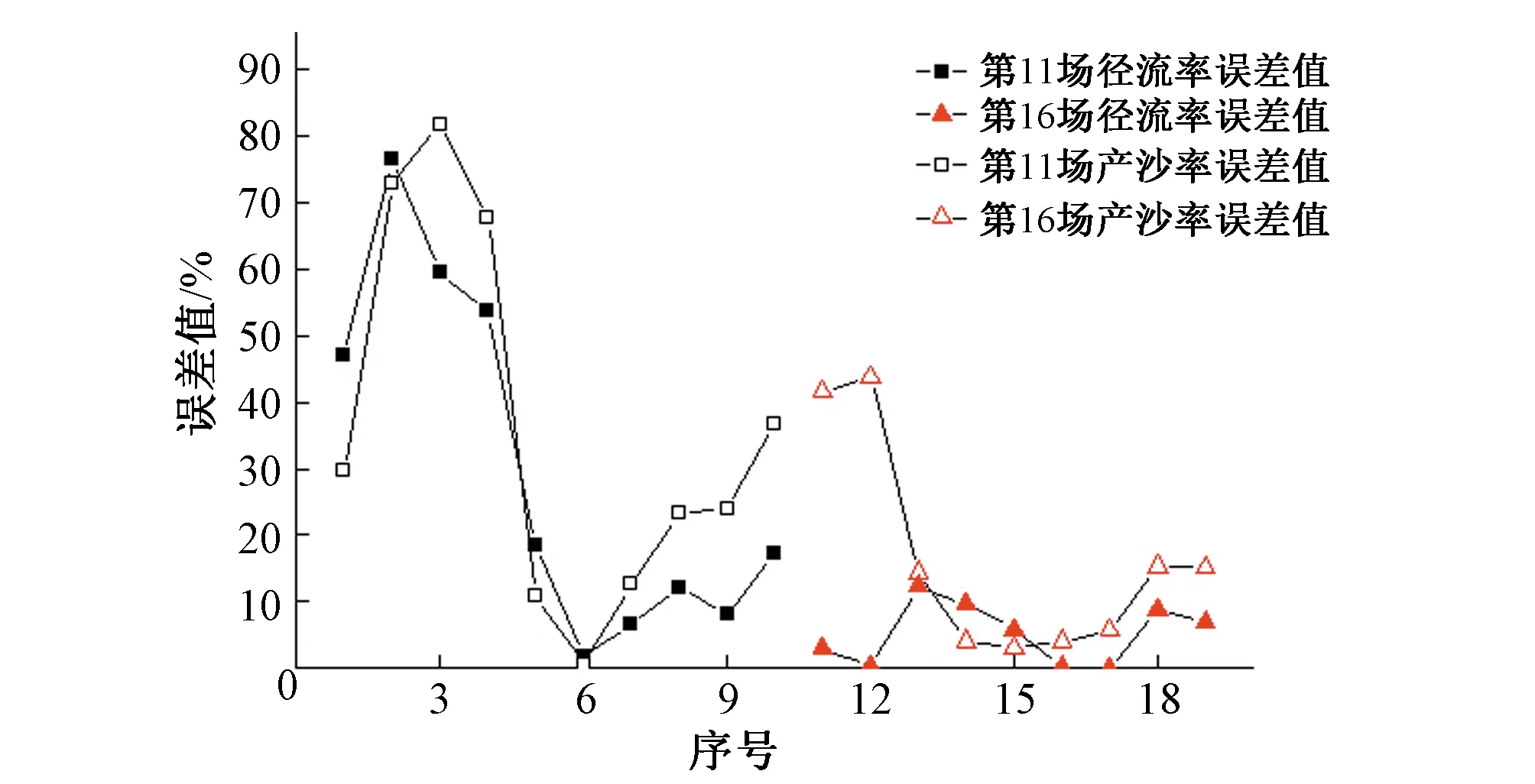
图4 实测值和预测值相对误差图

总体来看，径流率的预测效果要优于产沙率预测效果，可能是由于与产沙率相比径流的影响因素相对简单，随5个因变量变化的规律性更强，更适合进行模拟预测。

3 结 论

(1)变量对数化处理后，构建的偏最小二乘模型模拟精度和预测优度都较高，均达到了0.8以上，降雨初期坡面径流率和产沙率的相关性较好，相关系数达到了0.844。

(2)时间X3、坡度X1的VIP值结果表明，二者都是驱动因变量径流率Y1和产沙率Y2变化的重要因素，其中时间X3是最重要的影响因素；雨强对径流率和产沙率影响均较大，标准回归系数分别为0.408、0.341；初始含水率、剪切力的标准回归系数最大仅为0.145，表明二者对径流率和产沙率的影响都比较有限，坡度主要对产沙率起作用，标准回归系数达到0.412，对径流率的影响在模型中没有体现，标准回归系数仅0.039；

(3)精度分析结果表明，偏最小二乘模型在黄土坡面土壤侵蚀中适用性较好，对径流率和产沙率模拟和预测精度都较高，但与产沙率相比，径流率的预测精度更高，平均相对误差绝对值为18.313%，模拟预测的效果更好。

□