基于全寿命周期成本与神经网络的农业水泵经济性分析

樊明哲，彭小东，党晓强，徐 永，陈云良

(1.泸州职业技术学院电子工程系，四川 泸州 646005；2.西华大学能源与动力工程学院，成都 610039；3.四川大学水利水电学院，成都 610065)

0 引 言

水泵设备作为我国农业水利工程的重要基础设施之一，在农田调水灌溉中发挥着重要作用。在泵站新建工程和更新改造项目中，水泵设备的选购除了要考虑先进合理的技术以外，也需要考虑其经济性，这需要依据科学的分析比较来择取出最优方案[1-3]。长期以来，国内通常看重对水泵设备的初始购置费用，而较为忽视其在整个工作生命周期内所产生的费用，缺乏对水泵设备在整个生命周期内投资的精细化和经济性考虑。设备全寿命周期成本(life cycle cost，LCC)理论是基于设备资产的可靠性和长期经济效益，对设备在整个有效寿命周期内的全部费用进行核算，择取费用最小作为目标的一种现代工程经济学理念。LCC的核心思想在于，强调设备所具有的LCC费用是由设备运行前的初始成本和后续运行中的使用成本共同构成，从规划阶段就需要对设备整个生命周期的成本费用进行经济考虑。例如文献[4]提到在典型意义上，泵的初始成本仅占17%，而后续使用成本则为83%，对泵做全寿命周期成本经济性分析的重要性可见一斑。

近些年来全寿命周期成本的思想，在国内外很多行业的设备选购、更新改造决策、维修维护费用控制等方面获得了广泛关注和应用[5-12]，围绕LCC对国内水泵设备进行经济性分析与管理决策的研究尚少有报道。本文提出在项目初期对水泵设备进行基于LCC的经济性分析是科学投资关键所在，就其实现算法进行了初步的讨论和设计，引入BP人工神经网络来解决部分成本估算的不确定性问题，具体结合一个灌排站水泵设备选购的费用预算及经济比较的实例进行了算法思路说明。

1 水泵设备全寿命周期成本理论基础

1.1 全寿命周期成本管理的概念

全寿命周期成本的概念最早在20世纪60年代中期被美国国防部用于支持有关军事设施采购招标选择中的决策，随后在美国的公共服务部门得到了推广，70年代以后，LCC的概念在西方发达国家开始普及应用。1987年中国设备管理协会成立了设备寿命周期成本委员会，致力于LCC理论的研究和应用。LCC的概念在不同的国家以及不同的行业定义略有不同。例如参与制定文献[10]《Pump life Cycle Costs: A Guide to LCC Analysis for Pumping Systems》的美国能源部，其出版的(DOEO)413.3B条例将LCC定义为：“在项目规划、设计、开发、采购、生产、运营和维护、技术支持、资本重组等过程中发生的所有直接、间接、经常性、非经常性和其他相关费用以及不动产在其预期寿命内的最终处置的费用之和”。中国设备管理协会标准T/CAPE10001-2017对设备LCC的定义类似于此，但其进一步强调了 “应在设备全寿命周期的费用、绩效和风险三方面寻求综合效果最优”。

对设备进行全寿命周期成本费用分析的过程通常包括，首先需要对设备LCC费用的组成情况进行分析，针对费用支出性质的不同进行模块分解。例如针对水泵，在其整个寿命周期内，通常分解的模块包括：购置成本、安装调试成本、电能消耗成本、运行人工成本、维护维修成本、意外停机成本、环境影响成本、退役处置成本等；然后对分解后的各个模块费用进行建模和估算再进行迭加。由于要考虑设备运行年限内资本随时间的改变情况，如经济膨胀和利率等，这其中还需要应用一定的技术经济指标对LCC费用进行折算，常用的方法有净现值法、净年值法、内部收益率法和投资回收期法等；最后再基于LCC费用计算的结果及相关评价算法，进行分析决策。

1.2 水泵设备的全寿命周期成本方程

这里基于文献[4]和[10]的定义，对水泵设备LCC费用建模进行简要分析，方程如式(1)：

LCC=Cic+Cin+Ce+Co+Cm+Cs+Cenv+Cd

(1)

式中：LCC为水泵设备的全寿命周期总成本；Cic为初始购置成本，设备的购置费用通常包括水泵、管路以及辅助设施等；Cin为设备的安装和调试成本，包括对水泵的运输、水泵座基的建设、水泵安装固定、辅助系统连接、试运行及其性能评估验收、对泵站工作人员的培训等费用；Ce为能耗成本，包括对驱动水泵的原动机、控制器以及辅助设施等能耗成本的估算；Co为运行成本，是指与水泵系统日常运行监测相关的人工成本；Cm为维护维修成本，包括例行维护和事故维修所产生的人工费和设备费；Cs为停工停产损失成本，水泵系统意外故障所造成的停工停产损失费用；Cenv为环境影响成本，水泵系统对周围的环境影响成本比较有限，通常考虑的因素包括泄漏、噪音和一些运行中耗材处理的费用；Cd为退役处理成本，水泵或包含其系统在退役或更换时所需要的处理成本。

式(1)对应的LCC方程概念以及参数说明主要是思路框架上的介绍，源自国外相关文献对水泵设备LCC方程和模块划分的定义，阐述并非严谨细微，其定义的准确性有一定的局限范围。在具体采用过程中，需要结合参数实际含义和适用范围再进行分析。

1.3 LCC的经济评价方法-净现值法

在全寿命周期成本的分析中，通常将设备在整个项目计算时期内消耗的费用折算为净现值作为比较的标准。净现值是未来现金流的折现值与投资成本的差值，是一个比较资金在不同时间段内价值的基本工具，适用于项目的中长期投资决策分析[9,12]。各年度资金流折现的时间节点，通常取为项目投资的初期。本文后续算例分析中所做的预算和经济比较就是基于净现值法，计算公式如下：

(2)

式中：NPV为全寿命周期成本的净现值；Ci为净现金流入；Co为净现金流出；r为折现率；N为寿命周期，通常以年为单位；n为时间间隔，通常以年为单位。

如能依据式(1)和式(2)对设备在所完成的整个生命周期内每一笔支出进行准确记录并折算，那么迭加出的LCC值无疑是准确的，但实际中真正需要的是在设备生命开始之前了解LCC值。在对LCC成本预算时，针对式(1)中的各个因素进行逐一准确估算量化，通常并不容易做到，因此需要设计一定的算法思路来计算LCC值。

2 水泵设备的LCC算法分析

2.1 LCC费用的数据划分

这里具体结合水泵设备在规划阶段中的全寿命周期成本预算，做初步的通用算法讨论。数据划分思路如下：对于可以提供准确成本信息或能够较为准确建模的那部分成本由具体实际数据与具体计算提供；对于难以获取准确成本信息的其余各项成本则统一求和构成一个合并性的其他成本模块。其他成本模块数据依据已知类似工程的经验数据作为样本，与BP神经网络模拟预测结合求得。据此考虑式(1)中各个成本因素在测算分析中的不同特质，将各部分成本划分为购置成本C1、能耗成本C2、维护及维修成本C3以及其他成本C4四项费用。由参考文献[4]的分析，某类有代表性的水泵设备上述四部分各自的成本占比如图1所示，能耗成本和常规维护及维修成本构建了LCC的主要部分。

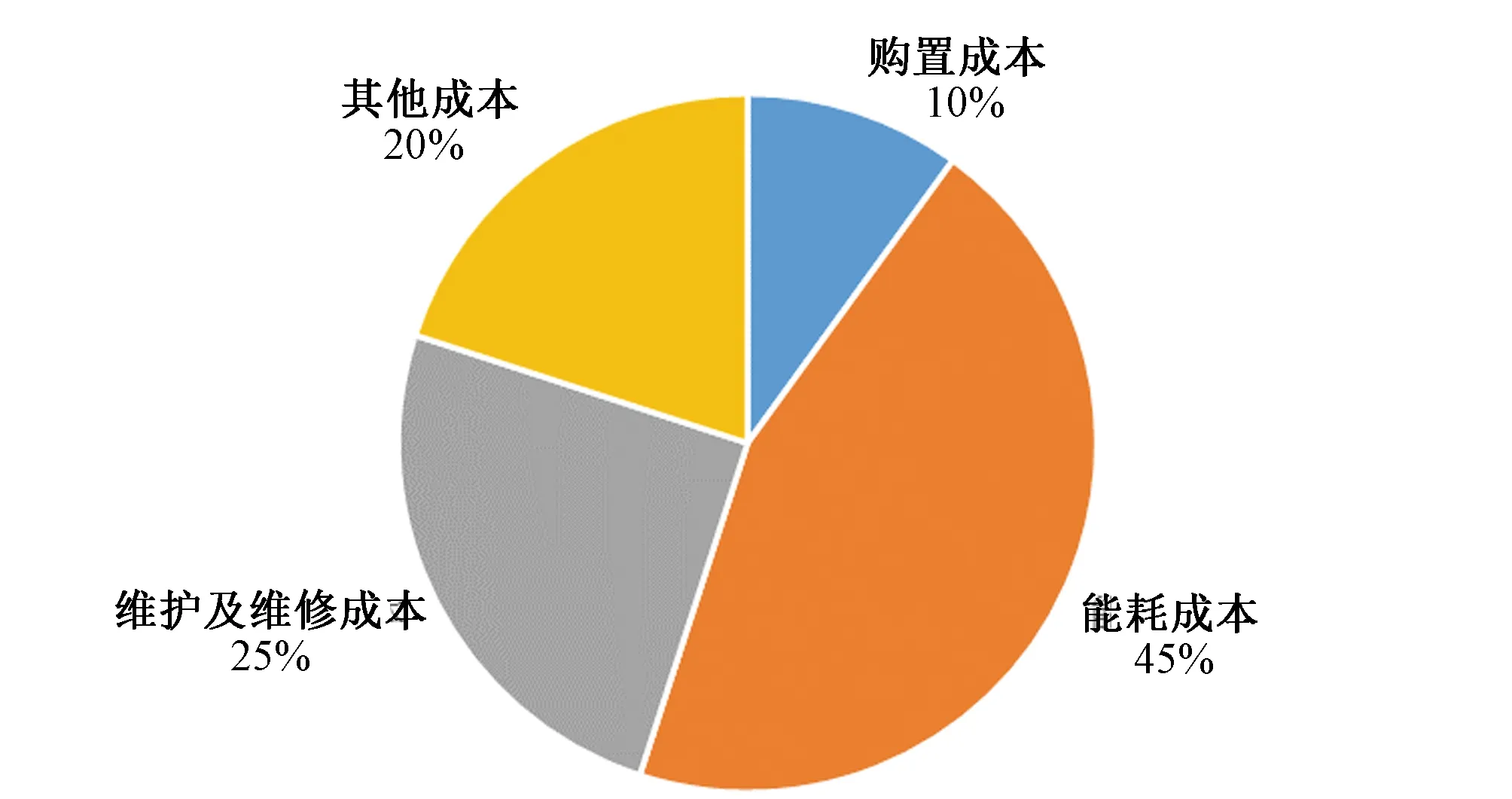
图1 某类典型水泵设备全寿命周期内各项成本费用构成

初步预算时进一步具体分析如下。图1中的购置成本C1为水泵设备的采购价格，通过询价则较为容易准确测算。水泵设备LCC费用中占主导地位的能耗成本C2与常规维护及维修成本C3两项，也可以通过已有资料建模进行估算。

能耗成本C2通过基于具体水泵参数对既定工作任务建模，由水泵轴功率P、年运行小时数Tn和设计工作寿命N以及电能单位单价R等已知信息，进行相对准确的估算。通常轴功率的确定：

P=9.81×QH/η

(3)

式中：Q为水泵流量；H为水泵扬程；η为效率。

如果暂不考虑时间对资本的影响，则：

C2=PTnRN

(4)

水泵的常规维护维修费用C3也是LCC中所占比例很大的一项开支，通常供货商会在其提供的维修手册中建议所供设备的维护周期和范围以及全寿命周期内故障维修的次数。其相关费用取决于维护维修工作的时间和频率以及使用材料的价格，也可以进行相对准确的估算。

其他成本C4含义丰富，这里进行说明；主要包括式(1)中的另外五项成本，如设备的安装和调试成本、运行成本、停工停产损失成本、环境影响成本以及退役处理成本等，这部分成本不易逐一准确细化建模估算。如在设计上配置同样效能的泵站，建设在不同地域的不同环境下，其设备的安装和调试费用以及人员的运行费用显然会截然不同。同样在具体项目预算时对整个生命周期内设备的停工停产损失成本、环境影响成本以及退役处理成本等做估计，也缺乏成熟的经验公式或理论算法。在初步预算时，这五项一起求和处理划入其他成本作为一个模块，由于这部分成本自身的难以确定性，基于神经网络的自学习智能映射进行求取。

此时LCC归算为4项费用之和：

LCC=C1+C2+C3+C4

(5)

依据全寿命周期成本中各模块数据的不同特点，采取不同的获取规则分别计算，保证了总成本数据在操作上的准确性与可靠性。如将其余各项成本求和作为一项成本处理的误差，很明显在理论上小于其各项成本分别误差代数相加之和；对于构成总成本中绝对优势份额的购置成本、能耗成本、维护及维修成本3大部分，从各自的准确计算算法上根本保证了其可靠性。

2.2 LCC的算法实现

在上述数据划分思想的基础上，算法中考虑资金的时间价值，再进一步将全寿命周期成本数据分为初始成本和后续成本两部分进行处理。一次性水泵的购置成本C1处于项目建设期的初始阶段，图1中的另3个成本模块构成LCC的后续成本。在算法实现中将后续每一年所消耗的成本费用等效处理为寿命周期内的年均成本费用Cnv，即认为每年的消耗大致相同。再考虑通货膨胀和利率等货币因素在时间上的影响，对后续每一年的成本基于项目初始阶段时刻，由式(2)做净现值修正为Cn，这样预算时的LCC成本等于购置成本C1与后续每一年成本Cn迭加之和，如式(6)所示。

(6)

式中：N为设备寿命周期；Cn为寿命周期内每一年后续成本的净现值，n=1,…,N。

后续成本年均费用Cnv的组成含义说明。其中的能耗成本与常规维护维修成本是水泵设备在寿命期内每年都需要支付较为稳定变化不大的后续成本，对其采用年均成本来等效处理容易理解。其他成本模块中的人力运行成本每年也是较为稳定的支出。另外4项，如安装和调试成本、停工停产损失成本和环境影响成本以及退役成本等，显然不是每年都需付出大致同等的费用，但其在全寿命周期总成本中所占比例较小，数据处理时统一将其年平均化包含在其他年均成本C4av支出内。这里依据Cnv定义的年均成本与后续每一年将实际支出的成本情况对比虽然都会有所差异，但可以看出对于全寿命周期总成本LCC的初步预算而言，其误差在有限范围内，这样处理对预算是有意义的。这里采用年平均费用或年平均消耗的思想，主要是从算法设计和便于净现值处理角度考虑的。

在神经网络算法具体实现时的取值，年均能耗成本C2av取值由设计说明书中的正常年工作任务进行确定，年均维护维修成本C3av取值由具体设备的维护维修准则进行确定。这样由C1、C2av和C3av三项作为BP神经网络的特征输入，其他成本模块的年费用平均值C4av作为神经网络的输出，得到了C4av具体求取如式(7)。

C4av=BP(C1,C2av,C3av)

(7)

此时可得，后续成本的年均消耗数值Cnv如式(8)。

Cnv=C2av+C3av+C4av

(8)

需要进一步说明的是，这里C4av的取值不是完全等同于前述C4中5项其他成本年均后的迭加，它在数据处理上的含义是“年均余下成本费用”的意思，即去除按上述规则的取值的C2av和C3av后，年均总成本费用Cnv剩余的一个成本，该具体数值在算法上并不是由迭加而来，而是由扣除而来。同样可以看出C2av和C3av作为已知量按上述规则的取值并没有准确代表能耗成本和常规维护维修成本的实际值，而是与各自实际成本值间存在着差异，这个差异值在算法中是包括在了C4av内。具体解释例如在水泵设备寿命的第一年与寿命的最后一年，完成设计中同样数量的年抽水任务，由于设备老化，后者能耗要比前者高，而这里对C2av的取值是取的设计值，即等同于正常情况下第一年的能耗成本，而这里所反映出的前后能耗成本上的差异值是存在于C4av内的。这样就明确了在BP神经网络算法实现过程中，样本取值以及输入值与输出值的具体含义和操作。

2.3 基于LCC的经济比较

基于LCC费用实现的预算，可以对不同厂家的设备进行经济比较。显然在相同的使用年限和工作成效情况下，水泵设备所消耗的LCC费用值越小，经济性越好。其实不同的厂家由于工艺、材质以及制造标准上的不同，其生产的水泵设备设计使用年限常会有所不同。这就需要在总费用的基础上，结合使用年限，综合考虑其经济性。这里引入年金的概念，作为其经济性评判依据。年金是指在一定时期内，每隔一定相等的时间，每次等额收付的系列款项，它能等值反映资金价值随时间的动态变化。作为一种资金等值计算方法，在针对不同营运年限、不同投资额的项目方案比选中，可以通过计算年金净现值来进行方案的经济性比较。

结合年金净现值的概念进行具体应用[13]，则在已知水泵设备的全寿命周期总成本费用净现值为LCC、折现率为r和全寿命周期时限为N时，年金净现值LCCA的计算公式如式(9)所示，

(9)

LCCA意味着每年所支付的资金，显然LCCA越小，经济性越好。如果全寿命周期时限N的选取发生了变化，那么每年所支付的LCCA年金随之动态变化。

3 BP人工神经网络

人工神经网络(Artificial Neural Network，ANN)是一种模仿人类神经网络生物特征的算法模型。ANN可以在数据的存储、分析、处理等方面进行人工智能模拟，适用于处理需要同时受多种因素和条件约束的非线性映射和模糊类的问题。BP(back propagation)网络是目前应用最广泛以及最为基础的一种多层前馈神经网络，其具体算法原理和函数解析相对复杂，这里不做介绍分析。BP网络的一个典型应用就是基于BP网络算法函数编写程序，通过输入已知的输入量和已知的输出量来训练网络，使其近似成为一个函数，这样就可以实现缺乏函数关系的映射，本文需要利用的就是这一特性。后续基于BP网络对其他成本模块年费用平均值 的预测求取，是在MATLABR2012a下完成的仿真。

在本文中，对BP网络的使用步骤如下：

(1)编写BP网络训练程序，设定函数的输入层到隐含层函数、隐含层到输出层函数、训练步数和误差目标以及学习速率这一系列基础数据。

(2)在编写BP网络程序过程中，输入所需要训练的样本数据，在内部运算达到期望的误差范围内时，BP网路训练完成。

(3)输入已知数据作为输入矢量，通过sim函数代入已经训练好的BP网络，然后由程序输出对应的预测量。

4 应用算例分析

基于前述算法，结合我国华东地区一座农业灌排泵站规划阶段中的水泵设备进行全寿命周期成本初步预算以及经济比较示例。具体需要选购的水泵设备型号为500ZLB-70立式轴流泵，其额定功率为55 kW，设计扬程5.5 m，流量0.6 m3/s。

由式(7)知，要求取其他成本的年平均值C4av，这里需要先构建训练用的样本如表1所示。表1中的购置成本C1由对应型号水泵网站市场报价得来。年能耗成本C2av具体结合同类排涝泵站能耗特点[2,4,15]，初步估算按照同类泵站国产同型单台水泵年耗电量为1.6 万kWh，电价0.5 元/kWh计算，年均电费0.8万元；年均维护成本C3av按能耗一半计为0.4 万元；其他成本计及的年均成本C4av为0.32 万元。表1样本中的能耗成本C2av、维护成本C3av与年均其他成本C4av，目前并不容易收集得到实际项目数据作为样本，这里的对应样本基于前述初步估算数据随机生成，同样适用于算法分析。表1中的前7组为国产水泵样本数据，后2组为进口水泵样本数据，进口水泵样本中的年均成本数据参照对应国产水泵并结合自身性能特点进行随机修正[16]。

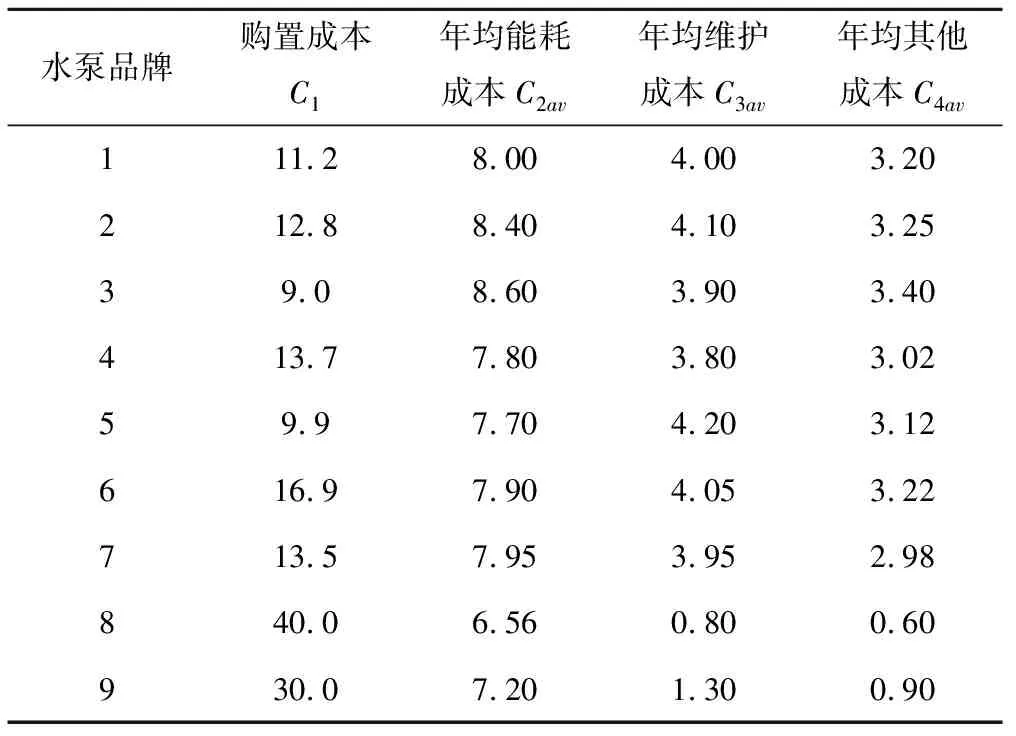
表1 500ZLB-70水泵训练样本数据 千元

表1中的C1、C2av和C3av为BP神经网络的样本输入，C4av是为BP神经网络的训练目标样本输出。根据MATLAB R2012a仿真，由图2可见，在迭代步数达到117次时，网络误差达到要求小于0.01。

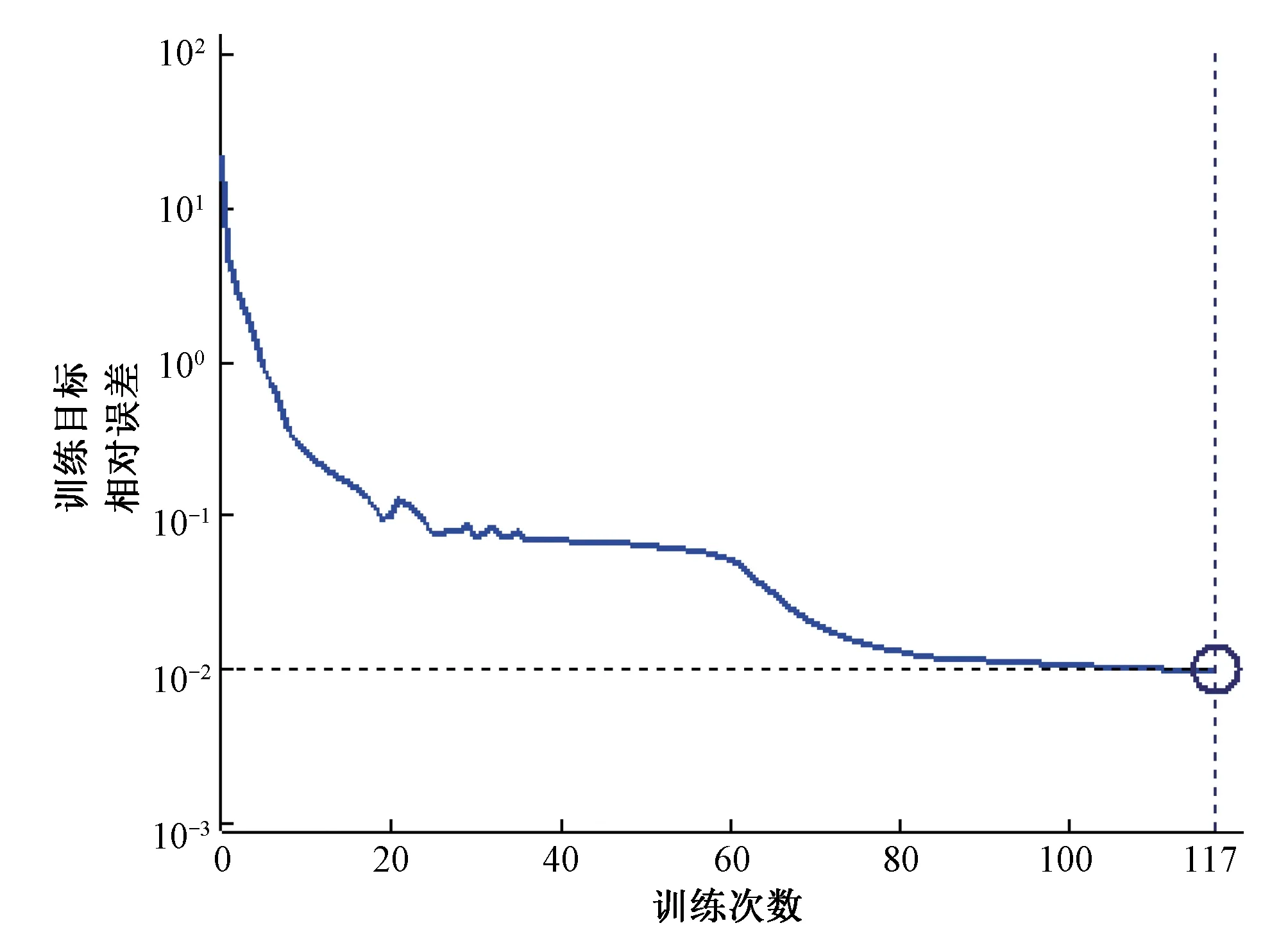
图2 BP神经网络的训练过程

基于上述训练后网络，输入两组数据对两个品牌水泵设备的其他成本年平均值C4av分别进行求取。一组为国产水泵设备G的数据，C1、C2av和C3av分别为(9.80、8.20、4.15)，输入程序如下：

Y=sim(net,P_test)

网络输出Y=3.563 8。

另一组为进口水泵设备F数据，C1、C2av和C3av分别为(35.00、7.00、1.10)，输出Y=0.670 1。

由已知的C2av、C3av和C4av，依据式(8)迭加，可得到后续成本总的年均消耗成本Cnv。基于净现值理论考虑资金成本投入的时间价值，对消耗成本Cnv数值在全寿命周期时限内，基于式(2)进行逐年修正取值折算至设备购置项目初期为Cn。这里算例中取年利率为8%，通胀率为4%，则折现率r为4%。再由式(6)将购置成本C1与全寿命周期内修正后的各个年度Cn值进行迭加，得到水泵设备的全寿命周期成本预算值。

设国产水泵设备G的工作寿命为8年，前述数据代入式(6)，则有：

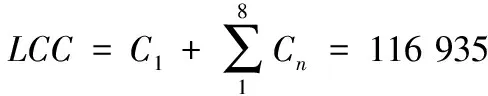
(10)

设进口水泵设备F的工作寿命为16年，同理计算，

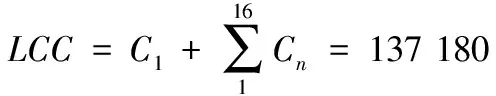
(11)

如上所述，这里完成了水泵设备全寿命周期内的成本预算，由于缺乏具体泵站中水泵全寿命周期成本实际值的资料，文中没有对准确性做进一步的对比验证分析。如果有多个品牌的设备可以进行选择，就需要进一步基于其各自的LCC值和一定的互斥方案经济评价方法进行比较取舍。例如对上述工作寿命不同的两种水泵设备，依据式(9)预算年金净现值分别如下。

国产水泵设备G年金净现值：

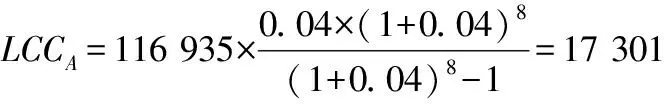
进口水泵设备F年金净现值：

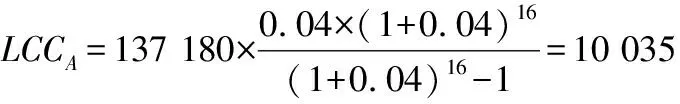
虽然水泵设备F总的LCC值要比水泵设备G大，但从年金等值的角度来看，其LCCA值比之要小很多，显然选购使用进口水泵F明显比国产水泵G更经济划算。

5 结 论

本文对灌排站水泵设备全寿命周期成本费用的实现算法进行了初步分析、设计以及示例，在部分成本数据的求取环节中引入了BP神经网络进行测算，结论如下。

(1)初步分析建立了一种水泵设备实现LCC计算的通用算法。重点涉及的技术创新和工作包括数据划分、年费用平均、费用求和的处理算法、人工神经网络引入以及净现值法修正和年金判据等。

(2)引入BP神经网络的人工智能属性，可以解决LCC中部分不确定性成本的难以测算问题。

(3)算例分析中将LCC费用算法结合水泵设备选购所进行的费用预算以及经济比较，系统展示了其可以提供科学的参考依据。

基于全寿命周期成本思想的经济性分析，可以为水泵设备相关的投资决策提供依据，目前在国内仍处于初步研究阶段，其潜在的科学性和应用价值还有待进一步工作。

□