粗糙集理论决策规则确定性因子在医疗诊断中的改进方法

何天荣

(丽江师范高等专科学校 教师教育学院，云南 丽江 674199)

粗糙集理论[1]是1种能有效处理模糊和不确定性知识的数学工具，在医疗诊断的应用中有很多成功案例[4-5].随着研究热潮的不断掀起，对粗糙集的研究无论是在理论方面还是在实践应用研究方面都取得了丰硕的成果，扩展型粗糙集模型的研究也取得很好的成果.将模糊集和粗糙集的有效整合用来处理不确定性问题比用它们各自处理取得更理想的效果[2-3].粗糙集理论在医疗诊断的应用中有很好成功案例[4-5].文中通过引入医生诊断病人是否患流感的决策表[6]：决策表中的条件属性为病人的临床症状(通过属性约简剔除了不重要的条件属性即症状“是否肌肉痛”，留下对决策属性有参考价值的条件属性，即症状“是否头痛”和“体温”状况，决策属性为是否患流感.利用决策表，最想要得到的是决策规则的产生，决策规则是医生临床诊断病情的依据.无论使用什么样的决策规则产生方法，都会产生2种决策规则：确定性规则和不确定性规则，对于确定性规则，没有任何争议，以本文决策规则为例，要么确定病人患流感，要么确定病人没有患流感，其可能性都是100%；但对于不确定性规则，其不确定性到底有多大是值得研究和改进的，本文通过以元素个数确定的决策规则的确定性因子的计算[6]，得出由这个方法产生决策规则中，不确定性规则对医生的临床诊断没有任何参考作用，原因在于有同样临床症状的病人患流感和不患流感的规则确定性因子完全相同且都是0.5，这说明这些患者患流感和不患流感的可能性都是50%，这对医生诊断病症没有任何参考作用，将在后面的例子中详细阐述.为了改进这一不足，引入了由大量历史数据确定的附带支持数的决策表[7]，由大量的历史数据确定的决策表，支持数是医生临床经验的总结，客观实际，同时它产生的不确定规则的确定性因子是不同的，根据规则确定性因子，在相同症状下可以确定病人是患流感的可能性更大还是不患流感的可能性更大.因此，改进的决策方法产生的决策规则中的不确定性规则对医生诊断病情同样有很好的参考价值.这样典型案列同样可以推广到其他病症的诊断上：比如可以把决策表中的条件属性“头痛”和“体温”改成“腰椎酸痛”和“小腹坠胀”就可以用同样的方法诊断女性病人是否患“盆腔炎”；将条件属性改成“头痛”和“鼻塞”诊断病人是否患“鼻炎”等等，当然这些支持这些病症的条件属性的重要性需要严格探讨.

对2种规则确定性因子进行对比后得到由支持数所确定的决策规则对医生诊断病人更具体有参考价值.

1 基本概念1.1 知识与知识库

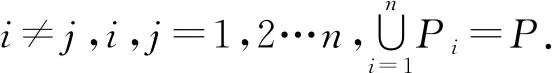
P上的一族划分称为关于P的1个知识库.

1.2 不可区分关系

定义2[6]设R是P上的1个等价关系，称为不可分辨关系，∀(x,y)∈P×P，若(x,y)∈R，则称x和y关于R不可分辨.P/R表示R的所有等价类(即P上的划分)构成的集合，记为[x]R，表示包含元素x∈P的R的等价类.1个知识库就是1个关系系统K=(P,R)，其中P为非空有限集合，称为论域，R是P上的等价关系.

1.3 信息系统

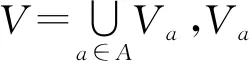
1.4 决策表

决策表[6]是一类特殊而重要的知识表达系统，假设S=(P,A,V,f)是1个知识表达系统，A=C∪D,C∩D=φ,A为属性集，要求A非空.其中，C为条件属性集，D为决策属性集.我们称具有条件属性和决策属性的知识表达系统为决策表.

借助决策表，最想要得到的是决策规则的产生，决策规则是进行决策的依据.在还没产生决策规则之前，可以先对决策表中的条件属性进行知识约简[8-10]，决策表中的有些条件属性是不重要的，可以通过属性约简的方法把冗余的条件属性去掉，这样可以得到对决策有重要参考价值的条件属性.但是，即使是重要的条件属性，他们的重要性也并非同等的重要.可以通过计算属性依赖度来确定条件属性的重要程度，即哪个条件属性对决策的参考作用更大，关于条件属性的重要性，将在另文中讨论.

下面将以医生诊断病人是否患流感的决策表(这里的条件属性是通过知识约简了的，对决策属性是有重要参考价值的，只要是对决策属性有参考作用的条件属性无论重要性多大都需要考虑)阐述决策规则产生的2种方法，并对2种方法进行对比，得出由由元素个数确定的决策规则中的不确定性规则对医生诊断病情没有任何参考作用，由支持数确定的决策规则更具有科学性，对医生诊断病情更具有参考作用.

2 由元素个数确定的决策规则确定性因子

通过医生根据条件属性“头痛”和“体温”诊断病人是否得“流感”(决策属性)的决策表说明由元素个数确定的决策规则的产生及确定性因子的算法.

例1 某些病人的决策表(如表1所示)，运用文献[6]确立性因子算法产生决策规则.

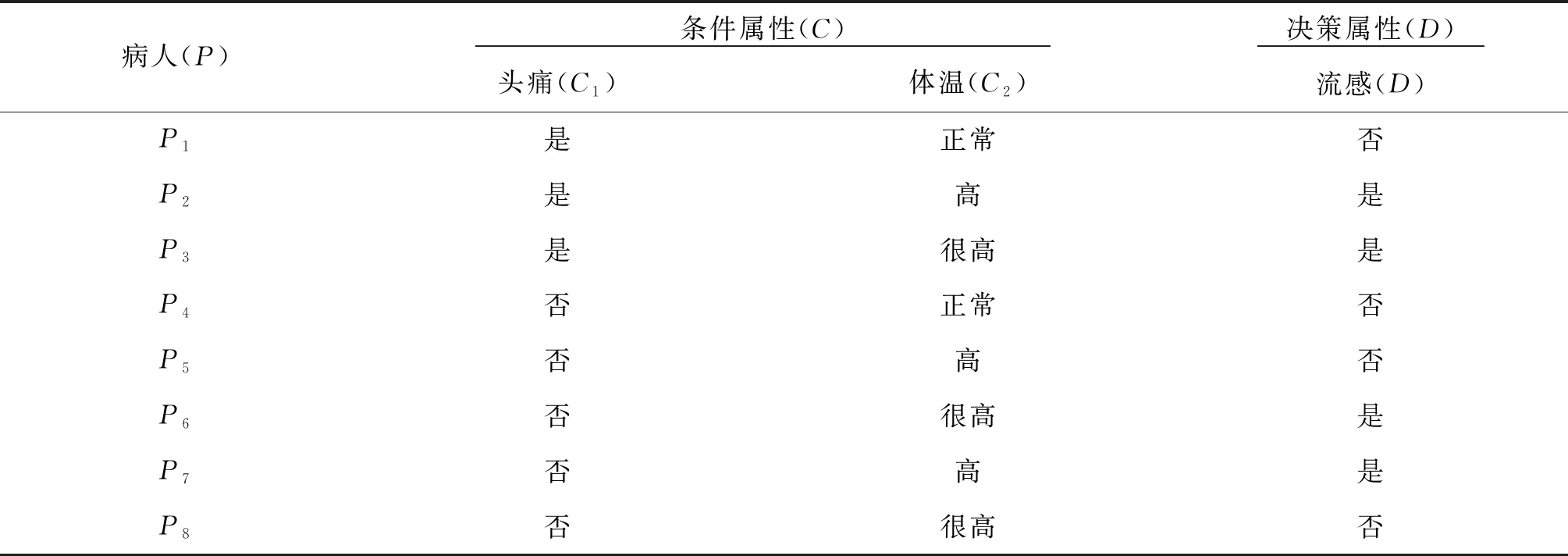
表1 流感决策表

S=(P,A,V,f)为一决策表，P为有限非空论域，且P={P1,P2,P3,P4,P5,P6,P7,P8}，

A表示属性集，包括条件属性和决策属性，A=C∪D,C∩D=φ，C为条件属性集，C={头痛，体温}，其中，C1={头痛}}，C2={体温}.

令集合Mi和Nj分别代表P/C和P/D中的各个等价类，des(Mi)表示对等价类Mi的描述，表示等价类Mi对各条件属性值的特定取值；des(Nj)表示对等价类Nj的描述，表示等价类Nj对各条件属性值的特定取值.

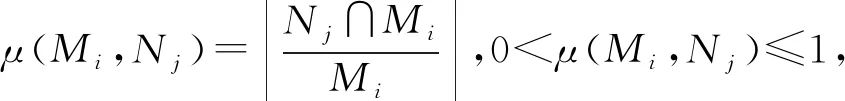
所得结论是，当规则确定性因子μ(Mi,Nj)=1时，决策规则rij是确定的，对决策有确定的参考价值；当0<μ(Mi,Mj)<1时，决策规则rij是不确定的，不确定性的大小由确定性因子的值决定.

由表1可得：P/C1={{P1,P2,P3},{P4,P5,P6,P7,P8}},P/C2={{P1,P4},{P2,P5,P7},{P3,P6,P8}}，P/indC={{P1},{P2},{P3},{P4},{P5,P7},{P6,P8}}，令P/C={M1,M2,M3,M4,M5,M6},则M1={P1}，M2={P2}，M3={P3}，M4={P4}，M5={P5,P7}，M6={P6,P8}.Mi,i=1,2,…6表示具有相同条件属性的病人.

令P/D={N1,N2}，则N1={P2,P3,P6,P7}表示患流感的病人，N2={P1,P4,P5,P8}表示不患流感的病人.

根据规则的确定方法，可以得到确定性的规则有以下4条.

r12:(头痛，是)且(体温，正常)→(流感，否)，可以根据规则确定性因子的算法证明;

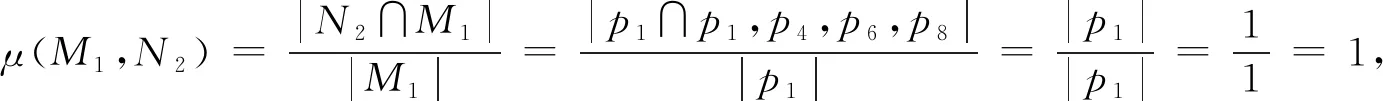
r21:(头痛，是)且(体温，高)→(流感，是)；

r31:(头痛，是)且(体温，很高)→(流感，是);

r42:(头痛，否)且(体温，正常)→(流感，否).

不确定性规则有也有如下4条.

r51:(头痛，否)且(体温，高)→(流感，是)，规则的确定性因子是0.5.可以根据规则确定性因子的算法证明如下.

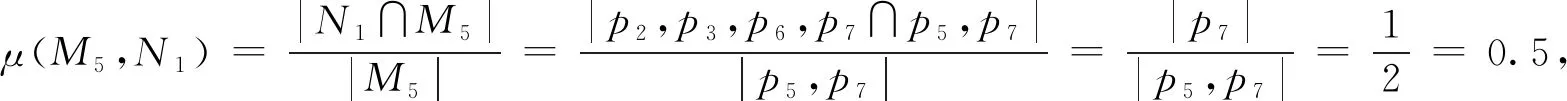
r52:(头痛，否)且(体温，高)→(流感，否)，规则的确定性因子是0.5，表示在病人没有感觉头痛但体温高(发烧)的症状下诊断为没患流感的可能性是50%；

r61:(头痛，否)且(体温，很高)→(流感，是)，规则的确定性因子是0.5.表示在病人没有感觉头痛但体温很高(高烧)的症状下诊断为患流感的可能性是50%;

r62:(头痛，否)且(体温，很高)→(流感，否)，规则的确定性因子是0.5.表示的是在病人没有感觉头痛但体温很高(高烧)的症状下诊断为没患流感的可能性是50%.

从上述由元素个数所决定的决策规则的确定性因子的确定方法可以看出，得到4条确定性规则，在病人“头痛但体温正常”及“头不痛且体温正常”的症状下，可以100%确定病人没有患流感；在病人“头痛且体温高”及“头痛且体温很高”的症状下，可以100%确定病人患流感，所以，对于确定性规则对医生的参考价值是没有争议的.但是，对于不确定规则，可以看到4条不确定规则的确定性因子都是0.5：在r51与r52这2条规则中，条件属性完全相同，而决策属性却是2种完全相反的结论，且2种完全相反结论的可能性完全相同.即“头不痛，体温高”的症状(条件属性)下既可以诊断为“流感”又可以诊断为“不是流感”，每1种可能性都是50%；规则r61与规则r62也是同样的道理:在病人“没有头痛但体温很高”的症状(条件属性)之下，诊断为“流感”的可能性是50%，诊断为“不是流感”的可能性也是50%.即不确定规则中同样的条件属性下得到的两种完全相反的决策属性的可能性恰好是一半的可能性.由此可见，这样的方法确定的决策规则，确定性的决策规则是毫无疑问的，但不确定性的规则对医生诊断病症是没有任何参考价值的，原因在于不确定性规则的确定性因子均为0.5.

为了改进这一不足，接下来引入1种附带支持数的决策表，通过支持数来改进规则的确定因子的算法，在这种算法下，不确定规则的确定性因子的值明显不相同，从而便于医生诊断病症时参考.表中支持数是由大量的历史数据(临床经验)确定出来的，客观实际.

3 由支持数确定的决策规则确定性因子

例2 附带支持数[7]的决策表(如表2所示)，运用改进的规则确定性因子算法产生决策规则.

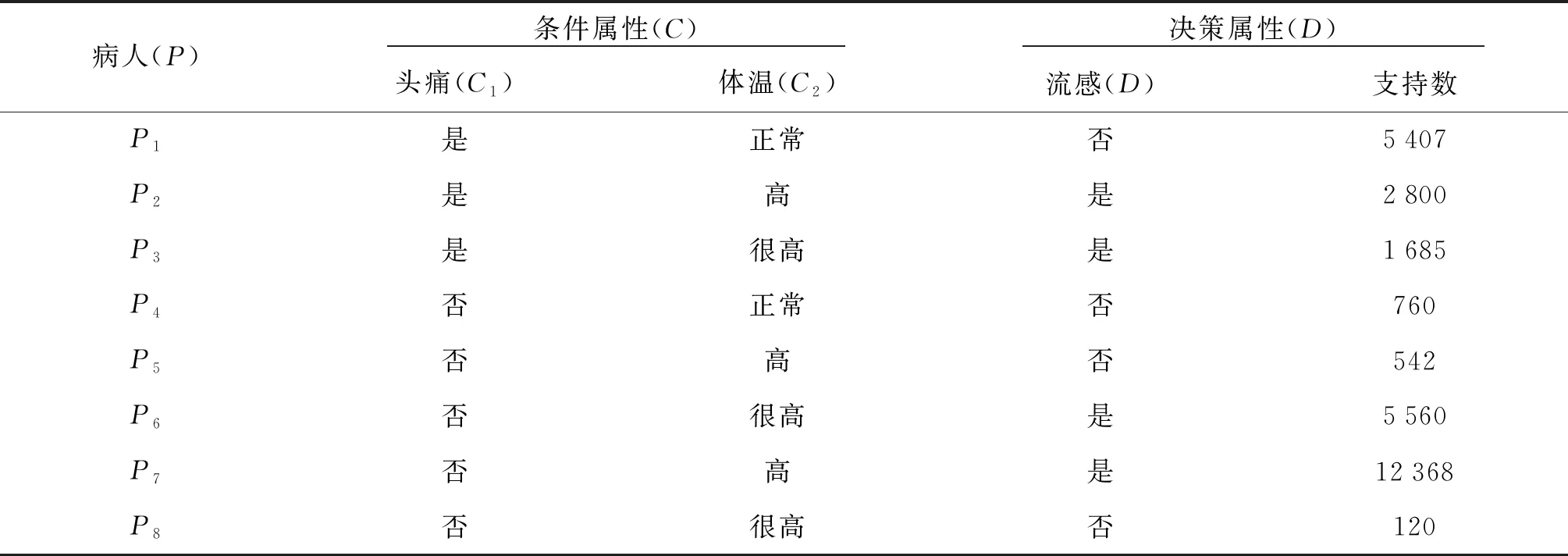
表2 附带支持数的流感决策表

类似于例1，令集合Mi和Nj分别代表P/C和P/D中的各个等价类，des(Mi)表示对等价类Mi的描述，表示等价类Mi对各条件属性值的特定取值；des(Nj)表示对等价类Nj的描述，表示等价类Nj对各条件属性值的特定取值.

由表2可得与例1同样的等价类：P/C1={{P1,P2,P3},{P4,P5,P6,P7,P8}},P/C2={{P1,P4},{P2,P5,P7},{P3,P6,P8}}P/indC={{P1},{P2},{P3},{P4},{P5,P7},{P6,P8}}，

令P/C={M1,M2,M3,M4,M5,M6},其中，M1={p1}，M2={p2}，M3={p3}，M4={p4}，M5={p5,p7}，M6={p6,p8}；令P/D={N1,N2}，其中，N1={p2,p3,p6,p7}，N2={p1,p4,p5,p8}.

决策规则定义为：rij:des(Mi)→des(Nj),Mi∩Nj≠φ，同样，产生决策规则的前提是集合Mi与Nj的交集非空，目的是为了确保规则确定性因子ν(Mi,Nj)>0.

通过这样的算法，可以得到与例1完全相同的4条确定性规则.

r12:(头痛，是)且(体温，正常)→(流感，否);

r21:(头痛，是)且(体温，高)→(流感，是);

r31:(头痛，是)且(体温，很高)→(流感，是)；

r42:(头痛，否)且(体温，正常)→(流感，否).

这里证明规则r21,其余规则可类似证明.

不确定性规则有也有4条，鉴于本算法比由元素个数确定的确定性因子的算法的优越性在于不确定性规则对医生更有参考价值，对4条不确定性规则都作详细证明：

r51:(头痛，否)且(体温，高)→(流感，是)，规则的确定性因子是0.958.事实上，

表示在病人没有感觉头痛但体温高(发烧)的症状下诊断为“流感”的可能性是95.8%.

r52:(头痛，否)且(体温，高)→(流感，否)，规则的确定性因子是0.042.事实上，

表示在病人没有感觉头痛但体温高(发烧)的症状下诊断为“没患流感”的可能性是4.2%.

r61:(头痛，否)且(体温，很高)→(流感，是)，规则的确定性因子是0.979.事实上，

表示在病人没有感觉头痛但体温很高(高烧)的症状下诊断为“患流感”的可能性是97.9%.

r62:(头痛，否)且(体温，很高)→(流感，否)，规则的确定性因子是0.021.事实上，

表示在病人感觉头不痛但体温很高(高烧)的症状下诊断为“没患流感”的可能性是2.1%.

由上述改进的规则确定性因子的算法，首先同样可以得到类似于例1的4条确定性规则，4条不确定性规则，这说明这个却则确定性因子的算法是合理的.对于确定性规则，不再赘述.改进的算法的决策规则的优越性在于不确定规则的确定因子不相同，即在同样的条件属性下2种相反结论的确定性因子明显不同，例如：规则r51和规则r52中，在“头不痛且体温高”的症状(条件属性)下诊断为“流感”(决策属性)的可能性是0.958，不是流感的可能性是0.042，说明在这样的症状下，病人有大约95.8%的可能性是患流感了，只有约4.2%的可能性是没患流感;同理，在规则r61与规则r62中，具有相同的条件属性“头不痛且体温很高”的条件下诊断为患“流感”的可能性大概是0.979而“没患流感”的可能性大概只有0.021，说明在这样的症状(条件属性)下诊断为“流感”的可能性约为97.9%，诊断为“没患流感”的可能性约为2.1%.同时可以看出，“体温很高”比“体温高”患流感的可能性更大.由此可以看出，“体温”是医生诊断病人是否“患流感”的一个很重要的临床参考依据，即在诊断病人是否患“流感”的条件属性中，“体温”最重要，其次才是“头痛”，这与由属性依赖度确定条件属性重要性所得的结论是完全吻合的，具体结论可以参看文献[2].由此可见，改进的决策规则方法，客观科学，无论是确定性规则还是不确定性规则，对医生诊断病症都有很好的参考价值.

4 结语

在粗糙集理论的决策表中，最重要的是决策规则的产生，决策性规则的产生关键在于决策规则确定性因子的算法.由等价类元素个数所确定的决策规则的确定性因子的算法，得出的结论是该方法产生的确定性规则对医生临床诊断病情有参考价值，但不确定性规则对医生的临床诊断病情没有任何参考价值，原因在于这种方法所产生的不确定性规则的确定性因子完全相同且都等于0.5，即在同样的条件属性下，得到2种截然不同的决策属性的可能性都是50%.为了改进这一不足，引入了由大量历史数据确定的附带支持数的决策表，改进决策规则确定性因子的算法，新的方法可以产生同样条数的确定性规则和不确定性规则，但是不确定性规则的确定性因子明显不同，即在同样的条件属性下得到的截然不同的决策属性的可能性是不同的且差异很大，医生完全可以根据规则确定性因子确定在病人发烧或者高烧的症状下极大的可能是“患流感”.因此，改进的方法产生的决策规则更科学，对医生尤其是缺乏临床经验的年轻医生诊断病情有很好的参考价值.