基于改进深度信念网络的旋转机械故障诊断研究

魏 乐， 张云娟

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

收稿日期：2020-03-19.

0 引 言

随着现代工业技术的不断进步，旋转机械日益向集成化、大型化、高速化和智能化的方向发展。滚动轴承和齿轮箱作为旋转机械设备的核心组成部分，被广泛应用于精密仪器、航空航天、汽车、机床、机器人等领域。但由于其运行工况环境恶劣，往往是旋转机械设备中较易损坏的零部件[1]。且一旦发生故障，与其连接其他零部件都会受到影响，进而危及整个设备的运行安全。因此，对于滚动轴承、齿轮箱等设备的状态监测与故障诊断，一直都是旋转机械故障诊断领域中的研究重点。

近年来，深度学习[2]技术被广泛引入包括故障诊断领域在内的诸多研究领域，其中，深度信念网络[3](Deep belief network，DBN)是Hintion在2006年提出的一种高效无监督学习算法，由若干个受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)堆叠而成，具有强大的特征提取能力，可以通过RBM的预训练有效解决传统神经网络参数随机初始化导致的容易陷入局部最优等问题。

李俊卿等[4]将DBN故障诊断模型应用于同步发电机，试验结果表明与传统故障诊断方法相比，DBN故障诊断方法能够取得更高的分类精度。陈保家等[5]利用DBNs对傅里叶变换处理后的振动信号频谱进行了故障诊断，与直接利用原始振动数据作为输入相比取得了更高故障识别准确率。钟诗胜等[6]提出了基于不均衡样本驱动的民航发动机故障诊断模型，通过采样技术将不均衡样本均衡化，利用DBN提取性能参数中的内部特征，实现了高维、不均衡样本的故障诊断。张朝龙等[7]利用混沌粒子群优化算法对受限玻尔兹曼机的学习率进行了优化，进一步提升特征提取的性能，与其他常用的特征提取方法相比，更好地实现了早期故障特征的提取。上述文献虽然对DBN模型性能进行了改进，但由于实际工业数据大多复杂多样，如果RBM可见层的输入被限制为二值，会对模型准确性造成一定的影响，采用能更好刻画现实数据分布的GBRBM模型具有很大的实用价值。

本文提出了一种基于改进的DBN模型的旋转机械设备故障诊断方法，引入高斯-伯努利受限玻尔兹曼机，并通过Adam优化算法和Droupout对网络训练过程进行优化。基于滚动轴承和齿轮箱的振动数据和改进深度信念网络建立了旋转机械设备故障诊断模型并进行了对比研究。

1 问题描述

故障诊断是对设备运行中产生的状态信息进行监测和处理，提取反映设备状态的特征，并根据此推断设备运行状态的过程，一般包括数据采集、特征提取、特征选择与优化、健康状态识别4个步骤。其中，特征提取和选择是故障诊断的关键步骤。

1.1 提出问题

传统依赖于复杂信号处理技术或专家经验等进行人工特征提取的故障诊断方法往往难以表征被测信号与机械设备之间复杂的映射关系[8]。其次，传统故障诊断方法中特征提取和健康状态识别两部分是分开进行的，降低了故障诊断过程的连贯性。而深度学习方法建立的深度学习模型具有强大的特征学习能力，能够从大量数据中自动提取、选择特征，进而学习到故障相关的隐含特征，建立特征与状态之间复杂、非线性的映射关系，从而实现故障诊断。

深度信念网络是深度学习方法之一，已经在图像识别、语音识别等多个领域得到成功地应用，但仍存在一些不足。因此本文主要解决的问题是提出对DBN模型的改进，提高模型收敛速度及识别准确率，并以滚动轴承、齿轮箱为仿真对象对模型性能进行验证。

1.2 研究对象

本文的主要研究对象为以滚动轴承和齿轮为代表的旋转机械设备。

滚动轴承是轴承中的一种重要类型，由内圈、外圈、滚动体和保持器4种元件组成。本文研究的主要故障类型为单点缺陷，即在其他相对未损伤的轴承表面上的单个局部缺陷，如凹陷、点蚀等。按照故障位置，单点缺陷可以进一步分为外圈故障、内圈故障和滚动体故障。

齿轮投入使用后，由于齿轮制造不良或操作维护不善，会产生各种形式的失效，常见的齿轮失效形式有：齿面磨损、齿面胶合和擦伤、齿面接触疲劳、弯曲疲劳与断齿等。

1.3 总体思路

为解决传统RBM对于非二项分布的数据重构拟合效果较差的问题，本文提出了GBRBM-DBN故障诊断模型。本文主要试验步骤如下：

(1)对故障数据进行连续截断处理，构建样本矩阵；

(2)划分训练、测试集，对数据进行傅里叶变换、归一化等预处理；

(3)构建模型并进行训练；

(4)输入测试集获得模型预测效果。

2 改进深度信念网络

2.1 高斯-伯努利受限玻尔兹曼机

受限玻尔兹曼机RBM是一个二分图结构的无向概率图模型，如图1所示，包含一个由m个神经元组成的可见层v和一个由n个神经元组成的隐藏层h，层内各个节点互不连接相互独立。

图1 受限玻尔兹曼机结构模型Fig.1 Structural model of restricted Boltzmann machine

由于传统受限玻尔兹曼机的可见层和隐含层都是二进制单元，即vi和hj的取值均为0或者1，而振动信号是一组连续的时间序列数据，二进制单元模型不利于连续数据的运算，所以本文在传统RBM模型中引入独立高斯分布的连续值来处理连续数据，把RBM的结构单元输出值限定在0～1之间的连续值。

高斯伯努利受限玻尔兹曼机(Gaussian Bernoulli RBM, GB-RBM)是由Krizhevsky和Hinton[9]共同提出的，用于建模非二项分布数据的玻尔兹曼机模型。GB-RBM是假设可见层变量为高斯分布，隐层变量为伯努利分布，其能量函数定义为

(1)

式中：ai为可见单元偏置；bj为隐单元偏置；σ为可见单元的高斯噪声标准差；wij为可见单元与隐单元之间的连接权重。

可见层和隐藏层的条件概率分别为

(2)

(3)

式中：N(μ,σi)为具有均值为μ和标准差为σ的高斯函数。

2.2 预训练

GBRBM与传统RBM一样均采用对比散度(CD-K)算法进行预训练。对比散度算法使用估计的概率分布与真实概率分布之间的K-L距离作为度量准则，对每个批次的训练样本进行k步Gibbs采样，以最大概率生成样本。

图2 CD-1算法原理图Fig.2 Schematic diagram of CD-1 algorithm

使用随机梯度上升法求取似然函数最大值，得到GBRBM网络参数更新规则为

(4)

(5)

bj=bj+η(〈hj〉data-〈hj〉model)

(6)

式中：η为学习率；〈·〉data和〈·〉model分别为真实数据的期望值和网络输出值。

2.3 反向微调

当RBM逐层无监督预训练完成后，将学习到的模型参数当做有监督学习的初始值，提供了输入数据的先验知识。在全局微调阶段，基于训练数据的类别信息，对比softmax分类器判定的类别，统计识别错误，并利用反向传播算法对DBN网络反向训练，微调各个初始连接权重。

2.4 模型建立

为解决传统RBM对于非二项分布的数据重构拟合效果较差的问题，本文提出了GBRBM-DBN故障诊断模型，该模型由一个GBRBM、二个RBM和一个softmax分类器组成，如图3所示。输入的训练数据作为底层GBRBM可见层的输入v0，其隐藏层输出h0作为第2层RBM的可见层输入v1，以此类推，通过CD算法实现GBRBM、RBM的逐层无监督预训练，确保特征向量在层内映射达到最优，最大化保留特征原始信息。最后将逐层预训练得到的特征信号通过一个全连接网络输入到softmax层，以交叉熵作为损失函数，采用Adam优化算法对网络参数进行自上而下有监督的反向微调，完成整个DBN网络的训练。

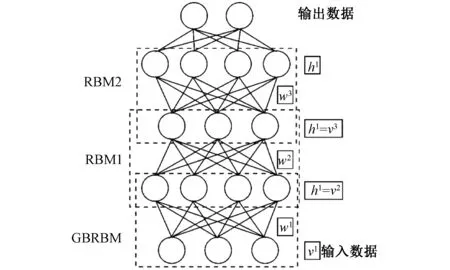
图3 改进深度信念网络结构Fig.3 Improve deep belief network structure

2.5 模型优化

为防止模型出现“过拟合”问题，引入dropout正则化对学习算法进行约束，在训练过程中以一定概率p随机丢弃一部分神经元及其连接，从而增强网络结构的鲁棒性，提升分类器的泛化能力。

为了优化网络性能，提高模型收敛速度，本文采用Adam[10]优化算法代替随机梯度下降算法来最小化损失函数。Adam是由Diederik Kingma和Jimmy Ba提出的一种将具有经典动量思想的RMSProp算法和L2范数思想相结合的优化算法。Adam算法能够利用梯度的一阶矩估计和二阶矩估计动态调整学习率，具有易于实现，计算高效，存储要求较低等优点。

3 仿真实例

3.1 实验1 滚动轴承故障诊断

3.1.1 数据集描述

本文采用的试验数据来自美国凯斯西储大学电子工程实验室采集的轴承数据集。试验通过加速度传感器采集深沟球轴承在0～3 hp 4种载荷下的振动数据，采样频率为12 kHz。每种载荷下，包括正常、内圈故障、外圈故障、滚动体故障4种类型。除正常状态外，每种故障类型又分为3种故障深度，故障直径分别为0.18 mm、0.36 mm、0.54 mm。本文选用采样频率为12 kHz的轴承驱动端振动数据作为试验样本，试验所得轴承振动信号共分为4种转速(1 797 r/min，1 772 r/min，1 750 r/min，1 730 r/min)，即在一个周期内的采样点数分别为400、406、411和416。为防止出现漏采情况造成的信息缺失，本文选择大于两个周期采样点数的1 024个点作为样本长度，对原始信号进行连续不重复截断，共得到5 600个训练样本和4 900个测试样本。具体样本设置如表1所示。

表1 滚动轴承数据集描述

3.1.2 数据预处理

为更好实现信号的表示与分析，对原始信号数据进行傅里叶变换转换为频谱数据集。由于原始振动信号幅值大小不一定在0-1之间，且样本中可能存在噪声、奇异样本等情况，因此需要对数据进行归一化处理，采用离差归一化方法。

(7)

3.1.3 参数设置

由于目前文献中对DBN模型层数和参数的选取尚无统一、准确原则，因此本文中的实验参数是根据经验按照网络结构逐级递减便于特征提取的原则进行设置的，再结合多次不同层数和迭代次数下DBN模型的训练结果不断调整择优设置，最终选择512-250-120-60-10的网络结构。各层神经元间连接权重由均值为0，方差为0.01的正态分布的随机数进行初始化，偏置初始化为0。预训练学习率ε为0.01，反向微调学习率α为0.1，动量0.9，dropout神经元丢失概率0.5，以交叉熵作为损失函数，最大迭代次数150次。

3.1.4 仿真结果及对比分析

将训练样本数据进行归一化后输入到GBRBM-DBN轴承故障诊断模型中，通过GBRBM、RBM逐层无监督预训练，组合低层特征形成更加抽象的高层表示，再利用顶层连接的softmax分类器进行分类，实验结果如图4所示。

图5中，坐标值1～10分别代表轴承的10种故障类别，对角线上阴影块代表每种故障类别的测试样本数目，其余格子中的数字表示误分类样本个数。由图5可知，除一个实际类别为0.54 mm的滚动体故障被错分为0.18 mm的外圈故障外，其他类别的分类准确率都在100%，取得了较好的分类效果。

图4 损失函数和准确率变化曲线Fig.4 Curves of Loss function and accuracy

图5 诊断结果标签分布 Fig.5 Label distribution of diagnostic results

为进一步验证本文方法的有效性及在诊断精度上的优势，分别对采用SGD算法和Adam优化算法进行优化的BBRBM-DBN模型(以下简称为DBN)进行了对比。实验结果如表2所示。

由表2可知，GBRBM-DBN-Adam和DBN-Adam模型在测试集上都取得了98%以上的正确率，而DBN-SGD模型的准确率则相对较低为95.29%。

本文方法除内圈0.18 mm故障外，其他的故障类别识别准确率均达到了100%，对早期故障具有较高的灵敏度，能够及时准确检测早期故障；DBN-Adam模型虽然平均正确率在98%以上，但在轴承内圈、外圈的早期故障类别上识别准确率较低，因此在早期故障识别方面，本文方法更具优势。

表2 不同算法滚动轴承故障诊断试验结果

图6为3种模型训练过程中正确率变化曲线，其中DBN-SGD模型收敛速度最慢且准确率最低，GBRBM-DBN-Adam与DBN-Adam训练效果相差不大，但首次达到90%准确率时，GBRBM-DBN-Adam迭代了10次，DBN-Adam迭代了19次；首次达到95%准确率时GBRBM-DBN-Adam迭代了17次，DBN-Adam迭代了26次，因此，在模型收敛速度上，本文方法优于其它两种方法。

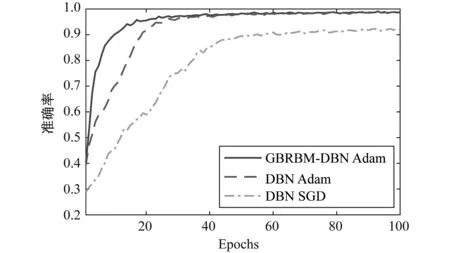
图6 训练正确率变化对比曲线Fig.6 Comparison curve of training accuracy change

3.2 实验2 齿轮箱故障诊断

(1)数据集描述

由于GBRBM-DBN-Adam和DBN-Adam算法在上述轴承故障诊断实验中效果相差并不明显，因此选用某齿轮箱数据集进行进一步的验证。本文采用的齿轮数据集源自江苏千鹏诊断工程有限公司旋转机械振动分析及故障诊断实验平台[11]，包括正常、断磨故障(大齿轮断齿和小齿轮磨损)、断齿故障、点蚀故障(大齿轮点蚀)和点磨故障(大齿轮点蚀和小齿轮磨损)5种齿轮箱状态数据。数据采样频率为5 120 Hz，每个齿轮箱状态记录由9个通道进行数据采集,所有的数据均在转速为1 470 r/min和转速为880 r/min下得到，为了验证相同转速下不同负荷时齿轮箱的运转状态，在880 r/min的工况下，分别加载0.2 A、0.1 A、0.05 A制动力矩输出电流。将试验数据样本以800个数据点为基准进行截断，最终共得到2 600个训练样本和600个测试样本。其中，训练样本2 600个，测试样本600个，样本设置如表3所示。数据预处理方法及参数设置方法与轴承数据集相同，由于篇幅有限就不再赘述。

(2)参数设置

模型结构均为400-200-100-50-5，输出层采用softmax激活函数进行分类，前向和后向学习率分别为0.01和0.1，动量0.5，最大迭代次数100次。

(3)仿真结果及对比分析

将归一化数据分别输入到DBN-Adam和DBN模型中，得到的训练及测试结果如图7、图8和表4所示。

图7 训练正确率变化对比曲线Fig.7 Comparison curve of training accuracy change

图8 训练正确率变化对比曲线 Fig.8 Comparison curve of training accuracy change

从图7、8中可以明显看出，GBRBM-DBN模型与DBN模型相比，不论是在单点故障的识别准确率还是混合故障的识别准确率都要更高、损失函数下降速度更快。

结合表4可知，GBRBM-DBN模型在测试集也具有较好的泛化能力，不论在训练集上还是测试集上都得到了更高的分类准确率，充分验证了本文所提方法的有效性和准确性。

表4 齿轮箱对比分类结果

4 结 论

(1)为解决传统RBM对于非二项分布的数据重构拟合效果较差的问题，引入高斯-伯努利分布的受限玻尔兹曼机，并建立了轴承、齿轮箱的GBRBM-DBN故障诊断模型，利用dropout技术、Adam算法对反向微调阶段进行了优化，最后，将提取到的信息输入到softmax分类器中进行故障状态的分类识别。

(2)将本文所提方法与经Adam算法优化的DBN及传统DBN算法进行了轴承及齿轮箱故障诊断对比试验，结果表明，不论在训练集还是测试集上，GBRBM-DBN都是准确率最高的，同时也是收敛速度最快的，相同迭代次数下准确率最高，充分说明了本文所提方法在旋转机械故障诊断领域中具有良好的可行性和可靠性。