基于模糊聚类算法的同调发电机分群

汪海

（湘西民族职业技术学院，湖南 吉首416000）

电力系统暂态稳定过程是一个动态过程，对系统进行Prony低频振荡分析时，需采集含有振荡特征的大量信息，故提取能准确辨识区域振荡模式和本地振荡模式的振荡信息尤为重要，通过分析电力系统运行方式下的同调发电机信息，可以在采集信息中得到表征振荡模式较强的少量振荡曲线，从而实现对系统主要振荡特征的快速辨识目的，本文做了进一步的探讨，运用模糊聚类算法将系统动态过程中存在相似动态行为的发电机识别分群。

1 模糊聚类算法的分析

文献[1]指出初始分组划分的不同不影响同调机群的识别结果，初始隶属度矩阵的选取对聚类结果影响不大，均可以得到正确的分组结果，且最终矩阵的数值相差不大。

在本文仿真分析过程中，发现模糊C 均值聚类的结果与初始隶属度矩阵的确定有关，主要思路为用模糊等价分组法得到模糊C 均值聚类的初始隶属度矩阵，然后得到机组分群结果，步骤如下：

1.1 数据标准化[2]

设原始数据矩阵为{x1，x2，…，xn}，其中xi=（xi1，xi2，…，xim），（i=1，2，…，n）。

1.2 建立模糊相似矩阵

目前电力系统规模较大，选择合适的标定方法对机组分群的结果影响较大，通过大量仿真分析，本文采用相似系数法中的几何平均最小法建立模糊相似矩阵。

1.3 聚类

本文基于模糊等价矩阵聚类法，引入传递闭包法，由于得到的模糊矩阵只是一个模糊相似矩阵，为了分组，将其改造为具有传递性的模糊等价矩阵，用二次法求出矩阵传递闭包，从而得到机组聚类图。

1.4 确定最佳阙值

本文采用统计量法加以分析，确定机组最佳分群，最大的统计量值对应的分组选为最佳分组。

统计量为

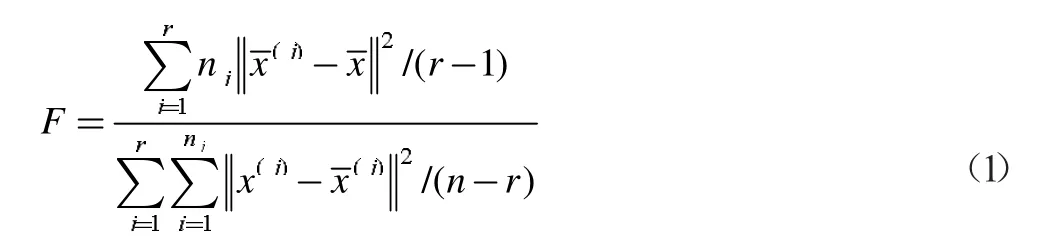
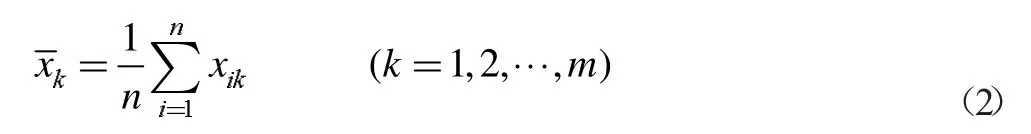
其中第k 个特征值的平均值为

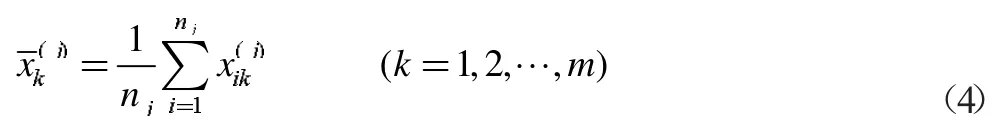
2 仿真与分析

采用四机两区域（4 机11 节点）系统，仿真数据取自文献[3]，扰动为母线8 处1s 发生三相短路故障，1.2s 切除故障，不采取其它紧急措施，仿真计算的时间总长度为10s，采样步长为100ms。

由于机组摇摆时功角曲线之间的相关程度反映了发电机的同调性，故本文以4 号发电机为参考机计算发电机相对功角曲线，分类时采用了基于模糊等价传递闭包法，用几何平均最小法进行计算标定，4 机11 节点系统机组聚类分组情况如图1所示。

从图1 中可以得到分组结果：

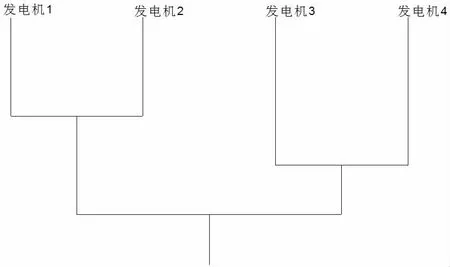
图1 4 机11 节点系统机组聚类分组

（1）分为2 组同调机群时，发电机1、2 为一组，发电机3、4为另一组；

（2）分为3 组同调机群时，发电机1、2 为一组，发电机3 为一组，发电机4 为一组；

表1 分组指标最优结果

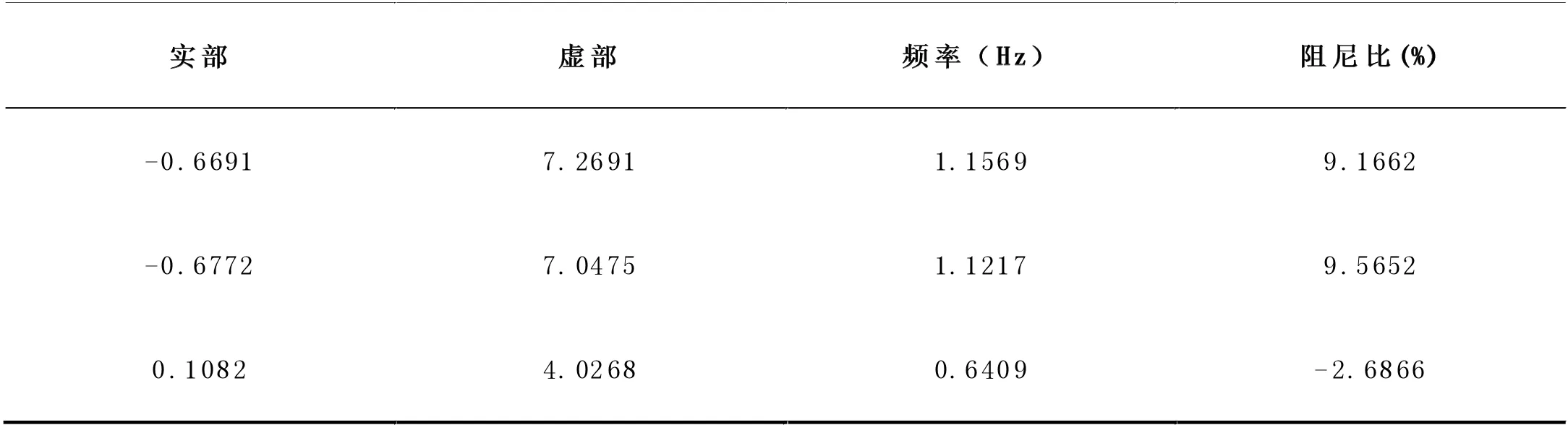
表2 电力系统综合分析软件PSASP 特征分析结果

（3）分为4 组同调机群时，发电机1 为一组，发电机2 为一组，发电机3 为一组，发电机4 为一组。

根据实际需要确定分组数，从表1 可知把系统分为2 组统计量值最大，确定为最优结果，当分组数为2 组时，选择1 号发电机与2 号发电机为一组，3 号发电机与4 号发电机为另一组，与电力系统综合分析软件PSASP 特征分析结果表2 一致，即1号发电机与2 号发电机为同一区域内机组，具有相同的局部模式，3 号发电机与4 号发电机为另一区域内机组，具有相同的局部模式。

当分3 组时，3 号发电机已从4 号发电机中分离出来了，在Prony 方法辨识结果中，观察到3 号发电机的主导模式为区域振荡模式，由此可见，通过选择3 号发电机的信号进行Prony 分析，可很好地观测到4 机11 节点系统的区域间振荡模式，采用各同调机群内部的表征性强的信号可辨识局部模式，验证了本文分析结果的正确性。

3 结论

本文在分析模糊聚类算法的基础上，探讨了发电机组的同调分组方法，即利用模糊聚类方法识别出电力系统的同调机群信息，可以初步确定辨识信号的选取范围，有利于在线分析振荡模式，最后通过对仿真振荡曲线进行分析，验证了该方法的可行性。