配电网有源电力滤波器的应用

刘金龙

（国网黑龙江省电力有限公司哈尔滨供电公司，黑龙江 哈尔滨150010）

随着现代电力行业的不断发展，非线性设备的使用所产生的谐波已经极大的污染了电力系统，并且会设备产生危害，因此，笔者将采用APF 对谐波进行监测，并且通过仿真对所提出的方法进行验证。

1 谐波的介绍

因为国际电压源是标准的正弦波，当非线性电流通过时则会失真，且电压也随之改变。谐波的具体定义如下：一个任意的周期信号，可分化为几个单一频率的叠加的正弦波，这些正弦波中，最低频率的一个称为基波，频率为基波频率n 倍的正弦波称为谐波[1]。

非正弦电流i（t），其周期是T=2π/ω，在切合狄里赫利的前提下，傅里叶级数形式是：

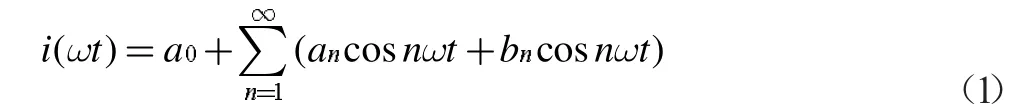
式（1）傅里叶级数表达式中，基波电流分量的频率为系统周期倒数，谐波电流分量的频率为基波频率整数倍[5]，电压谐波分析与电流谐波分析方法相同。

2 APF 工作原理与拓扑结构

2.1 APF 工作原理

作为新型消除谐波的装置，APF 不仅可以用于补偿谐波，同时也可以对无功功率进行补偿，有效避免了传统补偿谐波的方式，在图1 中，即为APF 基本原理图。

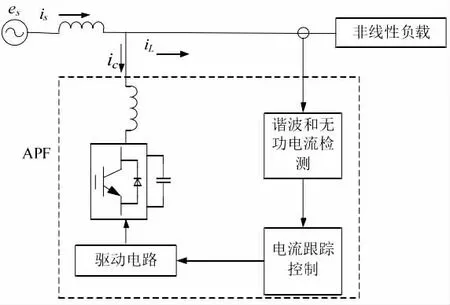
图1

在补偿谐波电流时，补偿电流的指令信号IX由APF 检测出对象负载电流iL的谐波分量ILA并将其反极性后得到。补偿电流发生电路产生的补偿电流ic与负载中谐波iLA大小相等、方向相反，两者相互抵消，谐波被消除。

2.2 APF 拓扑结构

在目前的电力系统之中，应用最为广泛的即是并联型APF，其根据谐波电流大小的变化，向系统中注入与谐波电流极性相反的电流，以此达到补偿消除谐波的目的。

3 瞬时无功功率理论

在20 世纪80 年代初期，日本学者首次提出瞬时无功功率理论，与传统理论相比，该理论全部是用瞬时值而非平均值所给出的。对下文所提出的谐波检测方法提供了理论支撑。

首先，假设三相电流的瞬时值分别为ia、ib、ic，其对应的三相电压瞬时值分别为ea、eb、ec，在空间直角坐标系内构建出其关系式为：

在平面正交系α-β 内，将两相电流值iα、iβ以及两相电压值eα、eβ分别进行同向分解可得如下关系式：

将对称三相有功以及无功功率分别记做q 和p，由此可以推导出功率与电压矢量e 的关系式为：

假设三相电压以及电流的表达式如下：

按上述理论，经计算可得：

不难发现，基于瞬时值的功率定义可以认为是传统定义的推广。

4 MATLAB 仿真分析

MATLAB 作为性能强大的数字编程软件，它可以进行建模仿真、算法设计等诸多工作，因此，在本文中，采用MATLAB 搭建并联型APF 仿真模型，仿真模型当中主要有谐波检测模块、测量模块、主电路模块以及控制模块所组成。在下表当中即为各个模块的参数设置。

表1

4.1 在电压无畸变情况下二者仿真比对

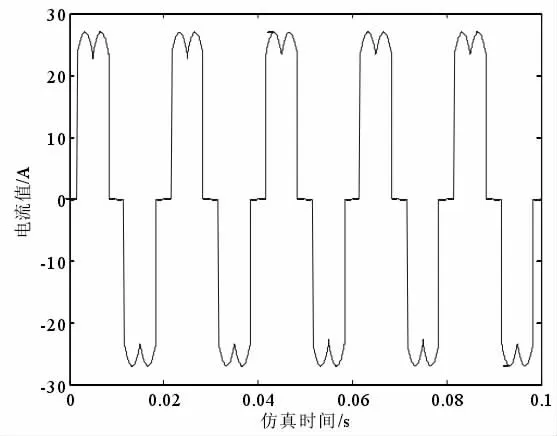
图2

在MATLAB 软件中设置其算法为ode23b，仿真时间设置为0.1s，通过对A 相电流分析不难得出，电流并非标准正弦波形，而是发生了较大畸变，分别采用两种检测算法进行谐波检测，获得基波波形图如下所示：

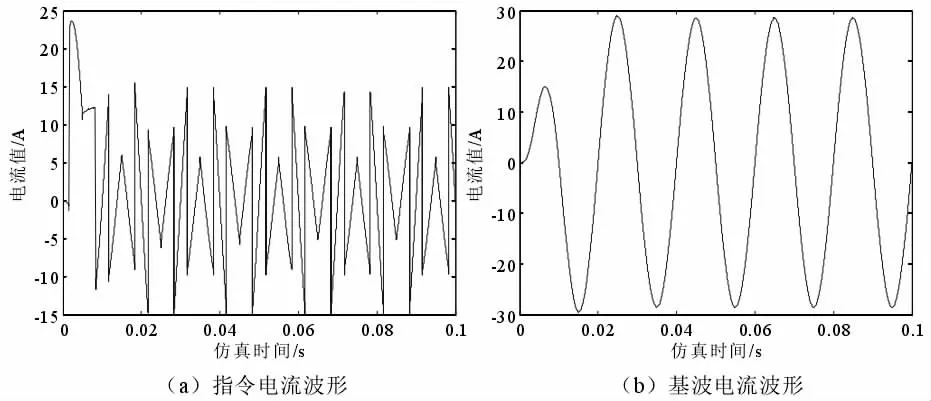
图3 P-q 检测算法波形示意图

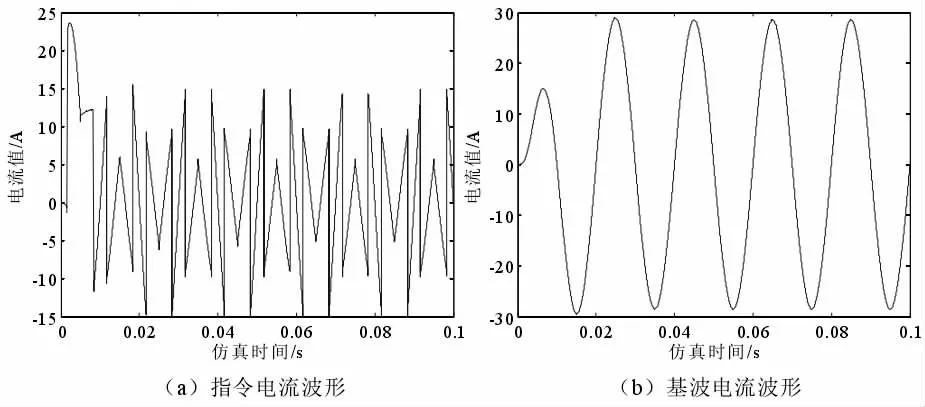
图4 ip-iq 检测算法波形示意图

通过比较二者检测算法波形不难发现，在电压不发生畸变的情况下，二者的检测效果大致相同。

4.2 在电压畸变情况下二者仿真比对

为了使电压发生畸变，在220V 正弦电压中加入了谐波电压，同样取其A 相波形参考，不难发现，其电压波形畸变严重，而图5 即为A 相电流失真后波形。

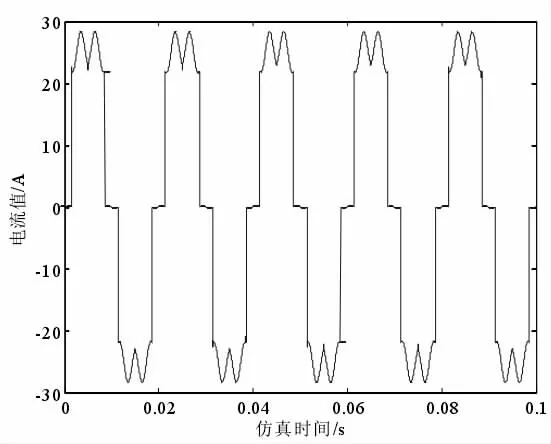
图5

分别采用p-q 检测法以及ip-iq检测法对畸变电流进行检测，仿真结果如下：

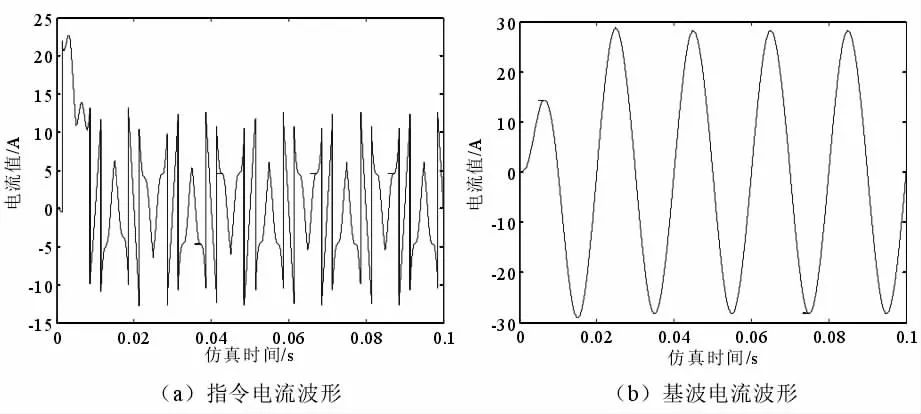
图6

图6 为采用ip-iq检测法所得出的波形，可以看出基波电流波形仍是标准正弦波型，畸变电流并未对其产生影响。

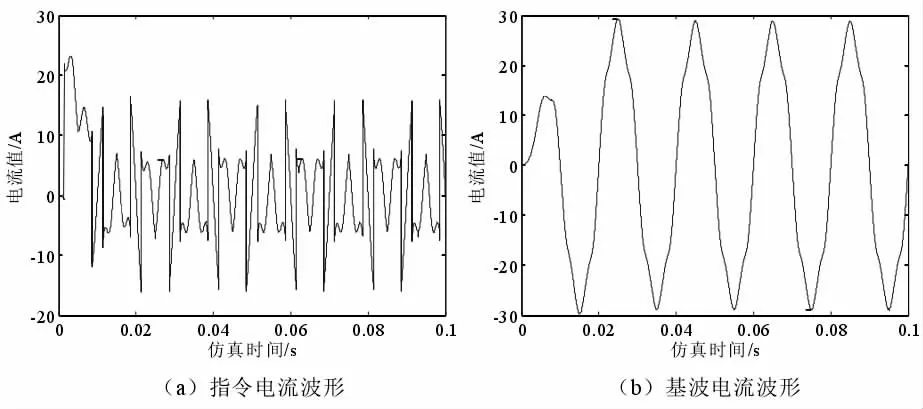
图7

图7 为采用p-q 检测法所得出的波形，可以看出由于受到畸变电流干扰，所得出波形并非标准正弦波形。

5 结论

通过对配电区有源电力滤波器分析介绍，以及对不同种谐波检测法进行分析比对，不难得出ip-iq检测法在电压畸变情况下的精确度远比p-q 检测法要高。因此ip-iq法具备比较好的检测效果。