基于Logistic 混沌置乱的图像加密算法

刘为超 刘义沛

（1、洛阳师范学院信息技术学院，河南 洛阳471000 2、重庆大学数学与统计学院2018 级数学与应用数学，重庆400000）

1 概述

数字图像媒体的特点：数据量大、数据冗余性强、相邻像素点相关性。图像加密算法分为一时空域的加密算法；二频域的加密算法。文献[1]进行改进提出二维像素字节位循环移位，国际同行称为TDCEA 算法，他们都是针对将原图像分割成8×8像素块内进行操作。文献[1-3，24]也是基于bit 位置乱研究的，文献[3]将M N 的原图像当作字节位级的M（8N）图像来操作，利用混沌置乱先进行行操作再列操作。根据目前图像加密分析算法的研究成果，以上大多数属于原图矩阵和密图矩阵间的双单射加密算法，其致命缺陷便是，对密码分析方法中的差分攻击抵抗性能非常脆弱。

2 算法研究基础

提出了一种基于字节位置乱的改进算法，借鉴了结合明文或者密文产生密钥的自适应加密思想。选择一个bit 位平面做为模板，生成参数做为密钥由Logistic 映射生成置乱序列并置乱模板bit 位平面，然后由模板bit 位平面分别和其它位平面进行异或计算。

由已经完成异或、置乱运算的上一个bit 位平面的数值产生混沌参数，来置乱下一个bit 位平面。最后将完成异或、置乱操作的8 个bit 位平面合成加密图像。仿真实验证明，算法具有操作运算简便而又不会降低加密安全性能的优点，是一种比较实用的图像加密算法。

混沌技术被广泛研究和应用，混沌映射是Li-Yorke 给出的Logistic 映射[8]。

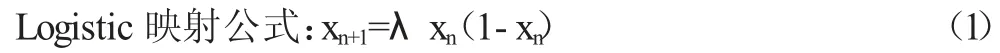
其中xn∈［0，1］，λ∈[0，4]。Feigenbaum 指出Logistic 映射分岔点的参数值λm（m=1，2，3…）形成无穷序列，并有一个极限值λ'=3.569945672…。当λ∈（λ'，4］时，Logistic 映射出现混沌现象。混沌现象具有对初始条件的敏感依赖性，行为是不可预测的，现广泛应用于图像加密算法中。

3 算法设计

图像uint8 格式的数据中，由每位像素8bit 位灰度值中相同位的数据构成的平面。一个图像矩阵共分为8 个bit 位平面，每个bit 位平面所形成的矩阵为位平面矩阵，记为G1、G2、G3、G4、、、G8。G1 为最低bit 位平面，G8 为最高bit 位平面。

加密过程：

Step1、G1-G8 中，在G1、G2、G3 中取一个作为基础模板参与异或加密运算。

Step2、根据（1）式要求产生混沌置乱序列S。截取S 中t 个数组成的混沌序列S={S1，S2，S3 St}。t 由下式决定。

其中，M，N 分别图像的行列数。此处300×8 是我们考虑到加密实时性要求，不再每个bit 位平面单独迭代产生混沌序列，而是统一生成一个混沌序列S，然后根据不同bit 位平面选取间隔不等的M×N 长混沌序列数组，必须保证一定间隔。

Step3、选取混沌置乱序列D1，生成由M×N 个混沌实数构成的数列。D1 对G1 进行混沌置乱操作。表示为D1={x1，x2，xM×N}

正排序D1 生成序列E1= {x'1，x'2，x'M×N}。D1 序列中元素在E1 中的位置序号构成集合F；E1 中元素在D1 中的位置序号构成集合F'，作为解密时运算。将G1（此处当做基础模板）位平面一维化成数组G1。（4）式为位平面的置乱加密；（5）式为位平面的置乱解密。

将G'1（G1）转化为M×N 位平面。

Step4、G'1 分别与其他位平面G2-8进行异或运算，生成新的G2-8位平面。

Step5、重复Step3 分别置乱G2-8，在置乱G2 时，D2 取S序列向后顺延（sum（G'1）mod 255）个元素的序列数组。同理Gn时Dn 取S 序列依次向后（sum（G'1）mod 255+sum（G'2）mod 255+ sum（G'n）mod 255）个元素的序列数组。

Step6、由经过分别异或、置乱操作构成的G'1-8重新组成密图矩阵G'。

解密过程：加密过程和解密过程是一对逆过程。不再详述。

4 实验结果与分析

4.1 敏感性分析

国际上通用“lena”灰度图像大小为256 256，matlab 环境下进行仿真实验。

测试用“像素数目改变率NPCR”和“归一化平均改变强度UACI”来计算比较。

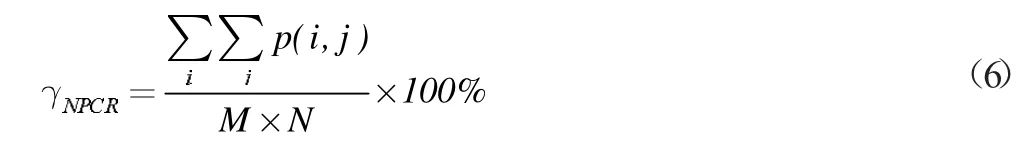
式（6）中P（i，j）表示：在两个测试密图差图中，如果点（i，j）值为0，表示对应像素点值相等则P（i，j）=1，否则P（i，j）=0。M，N代表图像矩阵的行列数。

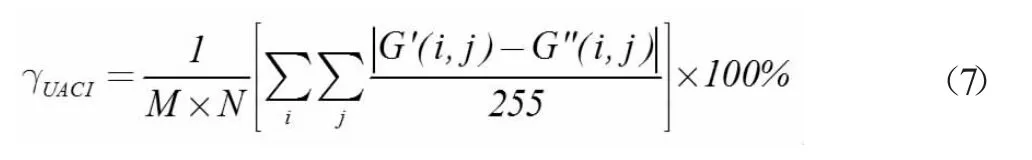
式（7）中G'（i，j）和G''（i，j）代表两个密图对应点（i，j）处的像素值。

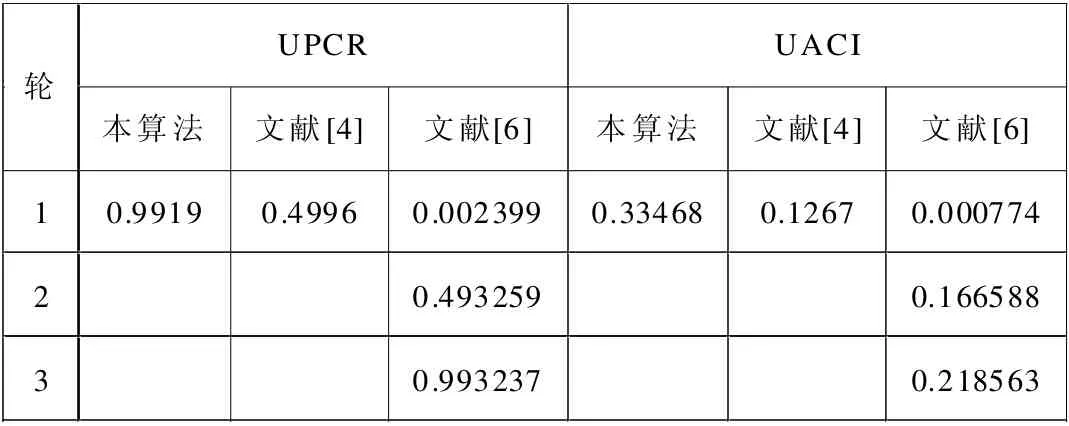
表1 NPCR 和UACI 分析

通过表1 可以得出，本文算法通过一次置乱加密即可达到很好的理想值，优于文献[4，6]。

4.2 相关性分析

正常的图像中大多区域色调基本是连续的，其相邻像素的相关性一般是非常高的，通常接近于1。效率高的加密算法会将这种相邻像素的相关性降低至接近0。计算相关系数的方法公式采用文献[4]中的公式。

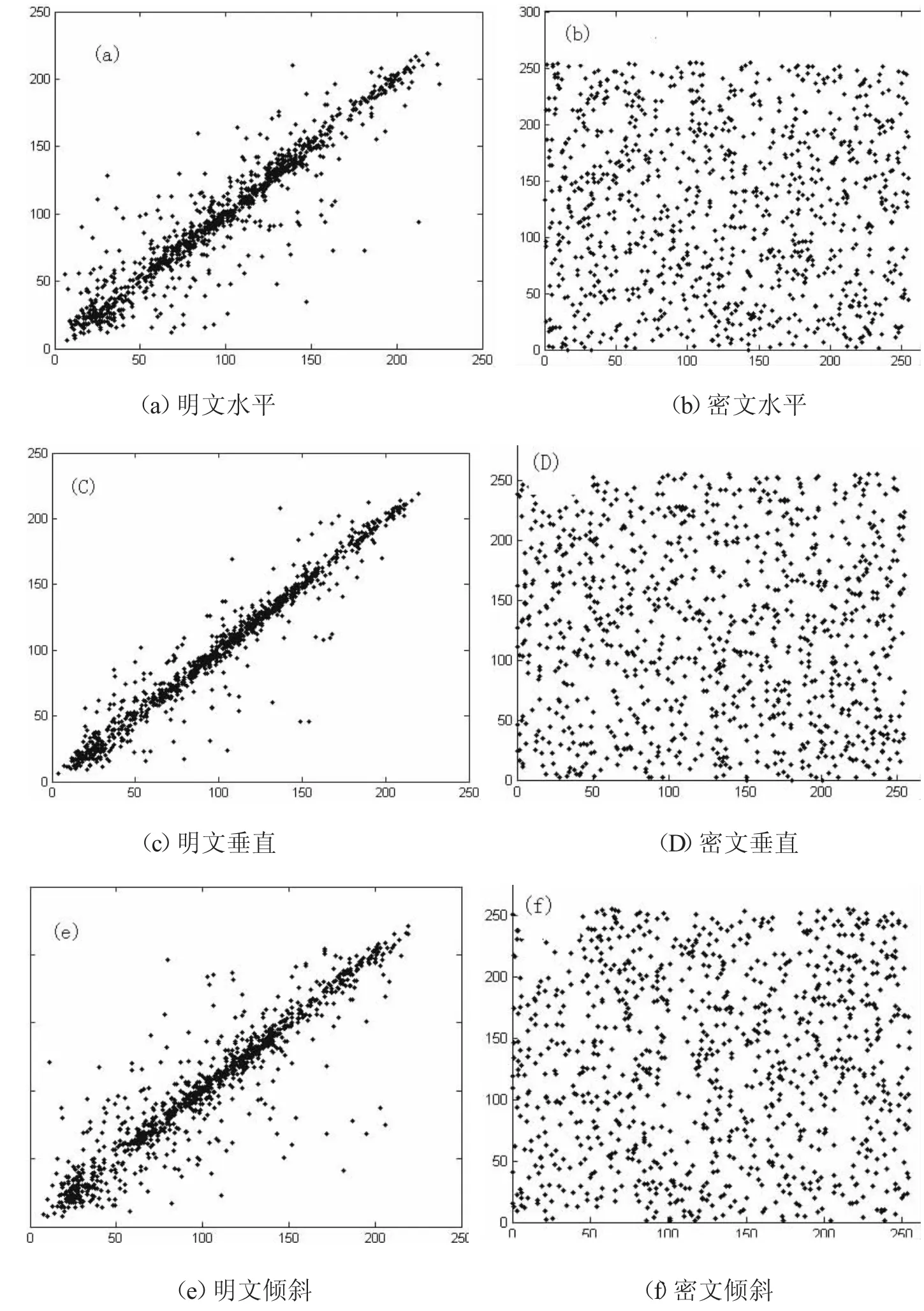
图1

本文在密图和明图中随机抽取1000 对相邻像素进行相关性计算比较，结果如图1 所示。水平方向，明文相关度为0.9487，密图相关度为-0.0131；倾斜方向，明文相关度为0.9354，密文相关度为0.0204；垂直方向，明文相关度为0.9701，密文相关度为-0.0165。结果可以得出，明文图像在三个方向上都具有很高的相关性。密文图像在三个方向上的相关系数基本接近0。

4.3 与同类算法的对比

文献[1-3]，他们的明文加密性能较高，但是他们远远没有达到雪崩现象要求标准（要求当一个像素值发生变化时至少密文会有50%以上发生变化）。文献[4，6]在差分分析方面达到了雪崩标准，但是需要经过多轮置乱。

密钥空间方面，本算法对图像每一层分别置乱，因此至少大于传统像素级置乱算法密钥空间的7 倍，同时加入各层之间的异或运算，密钥空间至少增加了数百倍。为了节约计算成本，本文采用一次置乱足够大，间隔选择置乱序列方法。

提出基于位平面Logistic 混沌置乱的图像加密算法解决了局限于图像矩阵间双单射的加密算法缺陷，数百倍扩大的传统置乱加密算法的密钥空间。