关注中考三角形的几个考点
李栋


[摘要]探讨中考中三角形的几个重要考点,即三角形的三边关系、三角形的三角关系、三角形的边角关系,可以使学生深刻认识三角形的边角关系,并能运用边角关系解答相关问题,提高学生基本的几何素养.
[关键词]三角形;中考;考点
[中图分类号]G633.6
[文献标识码] A
[文章编号] 1674-6058( 2020)35-0020-02
三角形的三边关系、三角关系与边角关系是各省市中考的重点,下面笔者对此做一探讨,
考点一:三角形的三边关系
三角形的三边关系,是指在所有三角形中,任意两边相加的和,必然大于第三条边,任意两边相减的差必然小于第三条边,这样我们可以通过已知三角形的两边长,求出第三条边的取值范围,进而求出三角形周长的取值范围,当第三条边取整数时,还可以确定第三条边的长,对于特殊三角形,如直角三角形,它的三边还符合勾股定理,等腰三角形,它的三边存在底边大于0小于二分之一周长,腰长大于0的规律.
[例1]解答下列相互关联的三个问题:
(l)观察图1,已知点P是三角形ABC的BC边上的一点,试比较BP+PC与AB+AC之间的大小关系.
(2)观察图2,当点P从三角形的一边上移到三角形的内部时,试比较C△BPC与C△ABC的大小关系.
(3)观察图3,当一个点P变化为两个点P1、P2,试比较C 四边形BP1P2C与C△ABC的大小关系,
解析:(1)根据三角形三边关系定理得出BP+PC< AB十AC.理由:三角形两边之和大于第三条边;
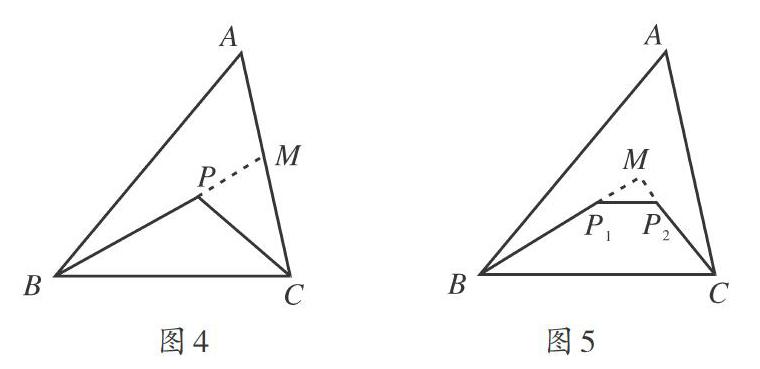
(2)可延长BP交AC于M,根据三角形三边关系定理得出:△BPC的周长<△ABC的周长,理由:如图4,延长BP交AC于M,在△ABM中,BP+ PM< AB十AM,在△PMC中,PC< PM+ MC,两式相加得BP+PC (3)分别延长BP1、CP2交于们,再根据(2)中得出的结论,可得出:四边形BPIP2C的周长<△ABC的周长,理由:如图5,分别延长BP,、CP,交于M,由(2)知,BM+CM< AB+ AC,又P1、P2 考点二:三角形的三角关系 三角形的三角关系,是指三角形的三个内角相加必为180°,即三角形内角和定理,已知三角形两个内角的度数可以求出第三个角的度数,此内角和定理决定了三角形最多有一个直角或钝角,最多有三个锐角,最少有两个锐角,因为三角形的内角与相邻的外角是互补关系,所以三角形的一组外角中,最多有一个锐角,最多有三个钝角. [例2]阅读下列材料并解答问题:我们规定,三倍角三角形是指三角形中,有两个内角的关系是三倍关系,当三角形ABC的三个内角分别为105°、35°、40°时,三角形ABC就是一个三倍角三角形,反过来,当三角形ABC是三倍角三角形,那么三角形ABC中必有两个角是三倍关系. (l)在图6中,∠O的度数为60°,BA垂直于∠O的一边OM,垂足为点A,判断△AOB是否是三倍角三角形,并说明理由. (2)在(1)的条件下,以A为端点画射线AD,交线段OB于点C(点C不与点O、点日重合).若△AOC是三倍角三角形,求∠ACB的度数. (3)图7,在三角形ABC中,DE平分∠ADC,且∠EFC与∠BDC互补,∠DEF与∠B相等,如果三角形BCD是三倍角三角形,那么∠B的度数是多少? 解析:(1)∵AB⊥OM,∴∠OAB= 90°,∴∠ABO=90° -∠MON= 30°,∵∠OAB=3∠ABO,∴△AOB为三倍角三角形; (2)。∵∠MON= 60°,∴当∠OAC= -∠AOB= 20°时,△AOC是三倍角三角形'..LACB= LOAC+∠AOB= 80°,当∠OAC=3∠ACO,即∠OAC= 30°时,△AOC是三倍角三角形.∴∠ACB= 90°; (3)因为∠EFC与∠BDC互补,∠LADC与∠BDC互补,根据同角的补角相等,得∠EFC=∠ADC,根据“同位角相等,两直线平行”,得AD∥EF,根据“两直线平行,内错角相等”,得∠DEF=∠ADE,结合已知中的等角,得∠B=∠ADE,再根据平行线的判定方法,得DE∥BC,根据题中的角平分线,得∠ADE=∠CDE,这样∠B=∠BCD.因为△BCD是三倍角三角形,所以应分两种情况讨论.(1)当∠BDC=3 ∠B时,根据三角形内角和定理,得∠BDC+ ∠BCD+ ∠B= 180°,所以5∠B= 180°,∠B=36°;(2)当∠B=3∠BDC时,7/3∠B=180°,∠B=540°/7 考点三:三角形的边角关系 三角形的边角之间最基本的关系是较大的边对的角也较大,较大角对的边也较长.三角形的边角关系还包括正弦定理、余弦定理及射影定理,它们是指在三角形中,每条边与它相对的角的正弦值相比,其比值都相等;每一边的平方,与其他两边的平方和减去两边与夹角余弦的积的两倍之间有相等关系;两边在第三边上的投影相加,刚好等于第三边,在直角三角形中,四个锐角三角函数讲的也是三角形的边角关系. [例3]阅读下列材料:在图8中,设三角形ABC的三边分别为a、b、c,那么三角形ABC的面积有如下三种表示方法,即1/2ab sin C、1/2ac sinB、1/2bc sinA 证明:在图8中,ADIBC,垂足为点D,在直角三角形ABD中,由正弦概念,得。inB:AD,所以AD:c.sinB,根据三角形的面积公式得三角形ABC的面积为1/2BC-AD=1/2ac sinB,如果利用∠C的正弦,可得三角形ABC的面积为1/2ab sinc;如果過点B作AC的垂线,可得三角形的面积为1/2bc sinA. (l)利用上述的三个结论,试证明sinA - sinB -sinC (2)如图9,已知三角形ABC中两个角的度数,即∠B为15°,∠C为60°,且一边AB的长为20√3,试求AC的长. (3)如图10,有一块三角形荒地ABC,在点B处观察点A时,射线BA的方向为北偏东75°,在点C处观察点A时,射线CA的方向为北偏西45°,且B、C两点的距离为18 km,那么三角形ABC的面积是多少?(sin 15°≈ 0.3,sin 120°≈ 0.9,√2≈ 1.4,结果取整数) 三角形的边角关系还包括三角形的一个外角等于两个内角的和,但是这两个内角不能与这外角相邻,三角形的三边关系、三角关系及边角关系始终是我们研究的重点,因为边与角是三角形最重要的两类要素,其他图形问题也要转化为三角形问题解决,因此,深刻认识三角形的边角关系,并能运用其边角关系解答相关问题,是初中生学习几何应具备的基本素养. (责任编辑 黄桂坚)

