基于NSGA-Ⅱ算法的左转待行区交叉口信号配时优化
贺文, 李硕, 夏文慧
(湖南大学 土木工程学院,湖南 长沙 410082)
1 引言
近年来,随着城市机动车数量的不断增长,道路资源有限,交通拥堵不断加剧。交叉口作为路网的瓶颈,其运行状态直接影响到路网的通行状况,其中,交叉口的左转通行对整个交叉口的交通状况影响较大。为解决交叉口左转车辆的通行问题,从提高交叉口资源利用率的角度出发,出现了左转车道拓宽设计、设置左转待行区、逆向可变车道等措施。其中,左转待行区的设计已广泛应用于各大城市,可以充分利用交叉口的空间,达到提高交叉口通行效率的目的。
目前,在GB 51038-2015《城市道路交通标志和标线设置规范》中对于待行区的设置方法较为明确。待行区设置的相关理论研究已较为完善,主要对左转待行区的设置条件、形式等进行了探讨。由于待行区的设置对交叉口车辆运行状态产生了影响,大量学者开始对设置待行区交叉口各项交通效益的评价指标进行研究,并建立相关的修正模型,为交叉口信号配时提供了理论基础。陈亦新、陈永恒等通过分析设置左转待行区的左转车道排队车辆从起步到驶离交叉口的释放过程,建立了左转待行区左转车道通行能力的计算模型;Yang Z等基于HCM通行能力和延误的计算模型,分析左转待行区设置后左转车辆的运行特性,分别通过设有待行区的累计车辆图和排队累计图,建立了左转待行区交叉口的通行能力模型和延误修正模型;倪颖等基于交通流波动理论,考虑在两种配时方法下, 左转待行区的设置对交叉口左转车道通行能力的影响,并推导出左转待行区设置后左转车辆平均停车次数增加的估算值;关桢等分析了左转待行区设置与饱和流率的关系,基于交通波理论,提出设置左转待行区交叉口最小绿灯时长的确定方法,并推导了停车率的修正模型。
与常规交叉口相比,左转待行区的设置提高了交叉口的通行能力,减小了延误和排队长度,但同时引发了二次停车问题,增加了车辆的停车率,因此,对于设置待行区的交叉口,左转车辆的停车率研究显得尤为重要。该文从左转待行区左转车辆运行特性出发,基于交通波理论,推导待行区设置后左转车辆增加的二次停车率,建立停车率的修正模型。结合交叉口的车辆延误,以平均延误和停车率为研究对象,建立双目标信号配时的优化模型,并采用NSGA-Ⅱ算法对配时方案进行求解。
2 交通波模型
2.1 交叉口车辆运行波动特性
左转车辆通过设置待行区的交叉口的运行特性如下:车辆由上游进入交叉口路段,在红灯期间,车辆陆续在交叉口第一停止线,即无待行区交叉口的停止线处停车,形成一次停车波w1;在同向绿灯启亮后,左转车辆起动进入左转待行区,形成一次起动波w2;然后车辆行驶待行区长度距离Lw,在第二停止线,即左转待行区的停止线处停车,形成二次停车波w1′;在左转绿灯启亮后,车辆驶离待行区,形成二次起动波w2′。左转车辆运行的时空轨迹图如图1所示。

图1 左转车辆运行时空轨迹图
2.2 交通波模型
由文献[8]可知,车流波速的计算公式为:
(1)
式中:q1、q2为车流前、后状态的流量(veh/h);k1、k2为车流前、后状态的密度(veh/km);v1、v2为车流前、后状态的速度(km/h)。
对比格林希尔治线性模型与格林伯模型,格林伯模型适用于较大密度的情况,交叉口交通流量大,采用后者作为交叉口的交通波模型较为合理。格林伯速度-密度对数模型表达式为:
u=umln(kj/k)
(2)
式中:um为最佳速度(km/h);kj为车辆阻塞密度(veh/km)。
左转红灯期间,车辆在交叉口第一停止线处陆续停车,式(1)中,v2=0,k2=kj,由式(2)得到一次停车波为:
(3)
式中:kd为左转车辆到达密度(veh/km),kd=qL/vd,其中qL为左转车辆到达率(pcu/h);vd为路段行驶速度(km/h)。
由于左转待行区的设置,左转车辆起动经过待行区长度Lw需要在第二停止线处停车等待,车流无法以饱和流率状态通过第一停车线。考虑交叉口的几何条件,左转待行区设置的长度一般为2~4个车辆的可停放长度,左转车辆在同向直行绿灯期间的运行状态类似于排队前进,参考文献[9],车辆运行可看作是以较低的加速度和减速度行驶。由图2可知:车辆1、2通过第一停止线,车辆3、4排队进行,车辆运行长度按待行区长度的距离进行排队,停车位置为1′、2′、3′、4′。车辆运行状态为:在同行绿灯启亮后,先起动加速到一定速度v,然后减速到第二停止线处停车,以速度v作为车辆的起动速度。

图2 左转待行区交叉口车辆运行状态
设左转待行区的长度为Lw,车辆的加速度为a1,减速度为a2,同向直行绿灯期间,单个车辆起动至停止的时间为t,可得以下公式:
(4)
推导可得:
v=2Lw/t
(5)
各个周期内车辆起动后的行驶车速为单个车辆起动速度的平均值。
(6)
同向直行绿灯启亮后,左转车辆进入待行区,式(1)中,v1=0,将式(2)代入式(1)得到一次起动波为:
(7)
3 停车率及延误模型
3.1 停车率模型
考虑不完全停车的情况,在车辆均匀到达的条件下,交叉口进口道的平均停车率按照Akcelic的计算方法建立模型表达式。信号交叉口的专用左转车道停车率计算模型为:
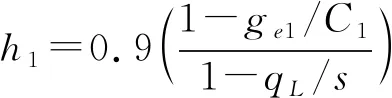
(8)
式中:ge1为设置待行区前的有效绿灯时长(s);C1为设置待行区前的周期时长(s);s为饱和流率(pcu/h),s=3 600h,h为车头时距(s/veh)。
交叉口设置左转待行区,在同向直行绿灯启亮后,排队等待的左转车辆需要由第一停止线行驶至待行区的第二停止线处停车,导致同向绿灯启亮前排队的车辆和起动波传递至排队末车前到达的车辆全部或部分需要进行二次停车,可通过比较左转车辆起动进入左转待行区所产生的起动波传递至排队末车需要的时间t′与同向直行绿灯时长tT的关系,推导停车率的增长模型。
两种情况下车辆起动时空轨迹如图3所示。

图3 车辆起动时空轨迹图
情况1:同向直行绿灯启亮后,第一停车线后的左转车辆开始起动,产生起动波并向后传递。如果在起动波传递至左转排队末车之前,左转绿灯已启亮,则同向绿灯启亮前排队的车辆和起动波传递至排队末车前到达的车辆,部分需要进行二次停车,部分只需一次停车。特殊情况,起动波传递至排队末车时,左转绿灯刚好启亮,则一个周期内到达的左转车辆都需要二次停车,起动波的传递时间即为同向直行绿灯时长。二次停车的车辆数为:
ΔN=w2tTkj,t′≥tT
(9)
情况2:同向直行绿灯启亮,左转车辆起动波传递至排队末车后,左转绿灯未启亮,则在起动波传递至排队末车前,到达的左转车辆都需要二次停车。起动波传递至排队末车后,左转绿灯启亮前,到达的车辆只需一次停车。二次停车的车辆数由两部分构成:① 同向直行绿灯启亮前累计排队的左转车辆数ΔN1;② 同向直行绿灯启亮后,起动波传递至排队末车之前,期间到达交叉口的左转车辆数ΔN2。
ΔN1=qLt横
(10)
式中:t横为异向车辆的通行时间(s),t横=C2-tL-A,其中tL为左转绿灯时长(s);A为黄灯时长(s)。
由图3可知:起动波传递至排队末车,与停车波在O点相遇。
(11)
式中:hs为车头间距(veh/m)。
(12)
由式(10)、(12)计算可得二次停车的车辆数为:
(13)
左转待行区交叉口的专用左转车道停车率计算模型为:
(14)
式中:C2为设置左转待行区后的周期时长(s);ge2为设置待行区后的有效绿灯时长(s)。
3.2 交叉口延误模型
左转待行区的设置对均匀延误和随机延误产生了影响。如图4所示,待行区设置前,车辆在tA时刻排队长度达到最大值,车辆开始释放,到tB时刻所有车辆释放完毕,三角形SOAB的面积即为左转车辆的均匀延误。
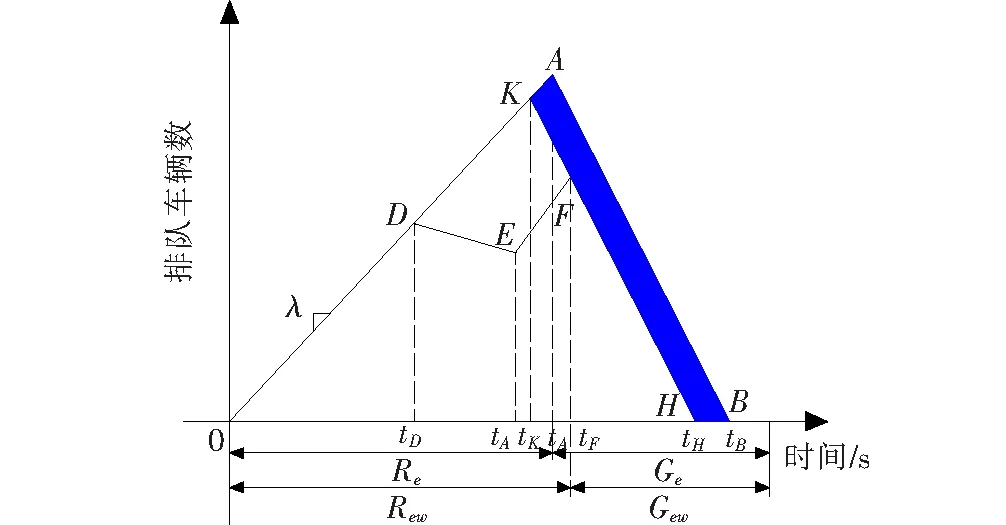
图4 待行区设置前后延误模型图
根据美国道路通行能力手册(Highway Capatity Manual 2010,HCM 2010),以均匀延误和随机延误作为延误的计算基础,模型的表达式为:
(15)
式中:x为设置待行区前的车道饱和度;λ为设置待行区前的绿信比;c1为设置待行区前的车道通行能力(pcu/h);T为分析持续的时间,取值0.25 h;e为信号控制调整参数,定时信号取0.5。
设置待行区后,车辆在tD时刻可进入待行区内停车等待,tF时刻车辆开始释放直至tH时刻车辆释放完毕。设置待行区后的均匀延误由两部分组成:停止线后的左转车辆的延误时间,即多边形区域SODEFH的面积;进入待行区内的车辆的延误时间,即多边形区域SDEFK的面积。阴影部分为设置待行区后车辆延误时间的减少值。平均延误的计算方法如下:
(16)
λd=(ge2+N/s)/C2
(17)
(18)
式中:xd为设置待行区后的饱和度;λ为设置待行区后的绿信比;c2为设置待行区后的通行能力(pcu/h);N为左转待行区可容纳的车辆数(pcu)。
对于随机延误,左转待行区的设置对有效绿灯时间和车道饱和度产生了影响,可采用:
(19)
平均延误为均匀延误d1和随机延误d2之和:
d′=d1+d2
(20)
4 信号配时优化
4.1 信号配时优化模型
关于交叉口交通效益的评价指标,常用的有通行能力、延误、排队长度、停车率等。其中延误作为评价交叉口运行状态的重要指标,其与周期时长、绿信比等指标密切相关。交叉口设置了左转待行区后,增加了二次停车率,交叉口对停车率的控制也尤为重要。该文以左转待行区交叉口为研究对象,以信号周期、相位有效绿灯时长为约束条件,建立交叉口控制延误时长最小、停车率最小的双目标优化模型,使总延误及总停车次数目标函数值取得pareto最优,达到优化的目的。
目标函数:
(21)
式中:qij为相位i通行方向j的车流流量;dij为相位i通行方向j的车辆平均延误;hij为相位i通行方向j的车辆平均停车次数。
其中,交叉口直行车道不存在待行区,对直行车流而言不存在二次停车的情况,直行车辆的停车率和车辆延误根据式(8)、(15)进行计算。
约束条件:
(22)
式中:ge为各相位绿灯有效时间;L为信号周期内的总损失时间;tmin为行人过街时长;ge(直行)为直行相位绿灯有效时间。
4.2 NSGA-Ⅱ算法设计
针对左转待行区交叉口的延误和停车率最小的双目标模型,采用NSGA-Ⅱ算法进行信号配时优化。NSGA-Ⅱ算法是Deb等在NSGA的基础上进行改进的,该算法提出了一种基于分级的快速非支配排序法,降低了算法的计算复杂度;提出拥挤度和拥挤度比较算子,使准域中的个体能扩展到整个域,并均匀分布,保持种群的多样性;引入精英策略,扩大采样空间,使得最佳个体不会丢失,迅速提高种群水平。算法的基本流程为:
(1) 基本参数的设定:对种群规模、最大迭代次数、交叉分布指数、变异分布指数等进行初始化。
(2) 编码:根据所研究的延误和停车率选择实数编码方式。
(3) 初始化种群,随机生成个体数为K的初始种群Pt,Gen=0,作为父代种群。
(4) 对父代种群Pt进行快速非支配排序和拥挤度计算,通过锦标赛选择、模拟二进制交叉、多项式变异3个基本操作,得到第一代子代种群Qt。
(5) 从第二代开始,将父代种群Pt和子代种群Qt合并,组成规模为2K的临时种群Rt,对该种群进行快速非支配排序和拥挤度计算。根据非支配关系以及个体的拥挤度,选取序值小的个体,同一序值条件下,选择拥挤度较大的个体,最终选出的最优K个个体组成新的父代种群Pt。
(6) 判断迭代次数是否达到预设的迭代次数,若是等于则结束运行,否则,跳转到(4),Gen=Gen+1。
5 实例分析
5.1 交叉口现状条件
该文以长沙市韶山南路与新建路交叉口为例,采取视频拍摄的方法获取数据。该交叉口为标准十字交叉口,各个方向分为左、直、右车道,各进口道有两条左转车道,设有左转待行区。信号控制为四相位控制,有专用左转相位,交叉口的现状数据如表1所示。
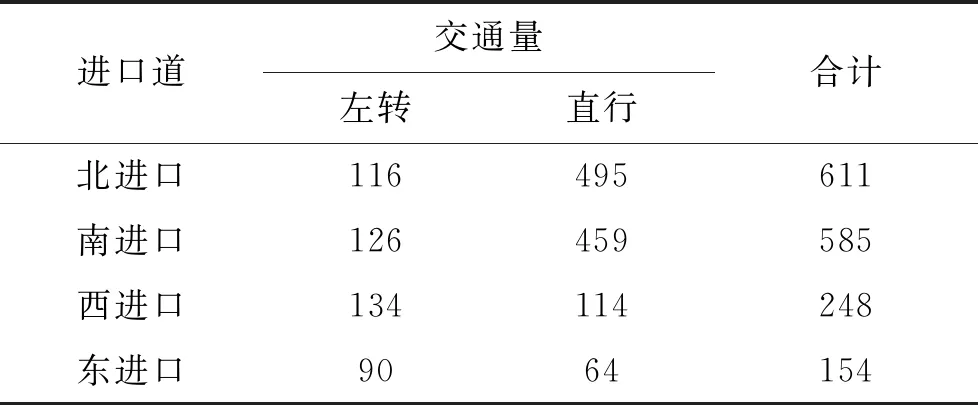
表1 交叉口交通流量 pcu/(15 min)
交叉口各进口道设置有交通岛,行人过街长度见表2。
信号相位方案如表3所示。

表3 交叉口信号相位
5.2 参数分析
车辆损失时间包括起动损失时间和清尾损失时间。对各周期内车辆通过停止线的时间进行统计。以南北进口道为例,计算可得左转车辆的损失时间为8.0 s,直行车辆的损失时间为5.9 s。因此,左转车辆对信号损失时间的影响达2 s,考虑南北直行相位之后设置2 s全红时间。
行人过街时长计算公式为:
(23)
式中:Lp为人行横道长度;vp为行人通过人行横道的速度,取值为1.2 m/s。
计算可得南北进口道行人过街时长为28 s,东西进口道行人过街时长为22 s。
5.3 起动波模型标定
该文采用实测数据对一次起动波进行标定,以南进口为例,待行区长度Lw=14 m,记录每组左转车辆进入待行区形成的起动波传递至队末车辆的排队长度,起动波传递至队末的时间,即从队首车辆起动到队末车辆起动所间隔的时间,可计算出起动波的平均传播速度。根据前文公式,整理车辆运行时间t,用模型计算可得27组数据。式(7)的模型计算值与实测值对比结果如图5所示。
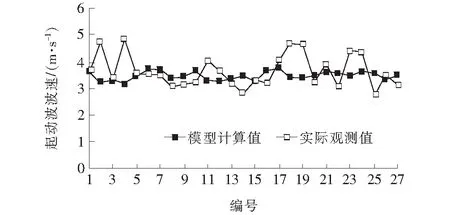
图5 起动波数据结果分布图
从图5可以看出:式(7)的模型计算值与实际观测值接近,模型计算值与观测值的平均偏差为:
因此,修正后的起动波模型是有效的。
5.4 结果分析
设定周期的取值范围,信号周期内的损失时间可通过数据处理获得,因此,在案例交叉口信号配时为四相位,并且左转与直行分流情况下,可将原约束条件转化为各相位的有效绿灯时间。
将交叉口划分车道组,不改变原有的信号相位相序,以车辆延误最小和停车率最小为优化目标,用NSGA-Ⅱ算法进行优化。由约束条件的处理可知,寻优变量为4个相位所对应的有效绿灯时间。采用实测数据,用矩阵进行表示,即各车道流量q为6×4矩阵,进口道流量Q为1×4矩阵。进口道的延误和停车率的矩阵形式为d(i,j)和h(i,j),i表示4个进口道,j表示4个进口道第几车道数,交叉口延误和停车率的矩阵形式为D和H,为4个进口道的加权平均和,最后将进口道延误和停车率加权为交叉口平均延误和平均停车率。
对算法的相关参数进行设置,种群规模为100,迭代次数为200,交叉概率为0.9,变异概率为0.1,调整变量的取值范围,求得pareto解如图6所示。

图6 NSGA-Ⅱ算法计算结果
由图6可知:对于交叉口信号控制多目标优化的非劣解集, 左转待行区交叉口的车辆延误与平均停车率相对而言是2个较为相互冲突的控制目标,交叉口的车辆延误最小和停车率最小不能在同一个点达到。
在国内外的研究中,通常将交叉口的延误作为评定交叉口运行状态的标准,考虑到此交叉口的各车道组的延误时间较长,信号配时方案选择车辆平均延误占优势的一组pareto解。因此,文中考虑将平均延误作为主要的评判标准。由计算结果可知:在停车率为(0.88,0.93)范围内,随着停车率的增加,交叉口的平均延误变化较大,停车率大于0.93的条件下,交叉口的平均延误变化不大,取停车率为0.93,平均延误为68.90 s/pcu,延误和停车率分别降低了13.61%、0.02次/s,得出的信号配时方案见表4。交叉优化前后结果对比见表5。

表4 交叉口信号配时优化方案

表5 交叉口优化结果对比
由表4、5可以看出:应用 NSGA-Ⅱ算法优化之后,信号周期时长由169 s变为125 s,车辆延误由79.75减少为68.90 s/pcu,降低了13.61%,停车率由0.95减少为0.93 次/s,降低了0.02 次/s。
6 结语
基于交通波理论,分析交叉口设置待行区后车辆的运行状态,建立车辆进入待行区的起动波模型,可为后期待行区车辆运行特征的研究提供一定的参考。以左转待行区设置后,引起的二次停车为研究对象,分析起动波在同向直行绿灯期间的传递情况,对交叉口停车率模型进行修正,为后文的信号配时优化提供了一定的理论基础。
该文以信号周期时长和有效绿灯时长为约束条件,以车辆延误和停车率为优化目标,建立双目标优化模型。用NSGA-Ⅱ算法对模型进行计算,对目标函数进行优化,得到一组以车辆延误目标相对占优的信号配时方案。由优化结果可知:信号配时优于现状,车辆延误和停车率较之现状有一定程度的降低,证明了优化模型和算法的合理性及有效性。

