裂缝性油藏缝间干扰界限初探——以JZS 油藏为例

王永平，朱志强，王欣然，刘 斌，张 伟

（中海石油（中国）有限公司天津分公司，天津 300459）

裂缝性油藏在国内占有较大的比重，产量贡献在我国油气生产中具有重要的地位，是油气上产稳产的重要方向。裂缝性油藏初期产量高，但由于其非均质性强且裂缝发育，注入水极易沿大裂缝优势通道流动，造成油井快速水淹，产量呈阶梯式下降，水驱动用程度差[1-8]。如果大小裂缝的渗透性差异较大，会产生强烈的干扰效应[9-10]，本文通过物理实验模拟大小裂缝同时存在时的干扰效应，并结合理论分析得出产生干扰的界限，最后通过数值模拟进行验证，对裂缝性油藏缝间干扰研究具有借鉴意义。

1 实验部分

1.1 基本参数及关键步骤

实验基本参数与JZS 裂缝性油藏基本一致，油藏温度75 ℃，实验压力18 MPa，实验仪器为常规水驱油实验装置。实验关键步骤如下：

（1）裂缝性岩心获取。本次实验所用岩心取自于渤海首个投入开发且规模最大的JZS 裂缝性油藏，用岩心钻取机获取裂缝性岩心柱塞。

（2）制作两块裂缝性岩心柱塞，一块岩心柱塞之间垫滤网模拟高渗通道，另一块岩心柱塞之间垫黄片模拟低渗通道。通过垫滤网与黄片避免裂缝“抱死”，同时对大裂缝与小裂缝进行有效区分（图1）。

（3）将制作好的裂缝性岩心分别放入两个岩心夹持器中，测量其渗透率；待饱和原油后，进行双管并联水驱油实验，记录两管较稳定时的产液量。

（4）用围压泵给不同的岩心夹持器施加不同的围压，从而控制裂缝开度，达到改变裂缝渗透率的目的，重复实验14 次以获取足够多的实验数据。

图1 实验用岩心柱塞照片

1.2 实验结果统计和分析

图2 中绿色点为实验所测得的不同渗透率级差所对应的大裂缝分流量数据点（表1），黑色虚线为根据达西公式计算的不同渗透率级差条件下的大裂缝分流量曲线。从图中可以看出，当渗透率级差大于2.00 时，受大小裂缝之间干扰的影响，大裂缝的分流量已经开始偏离按照达西定律计算的曲线，且渗透率级差越大，大小裂缝之间的干扰越严重，偏离达西定律计算的曲线越严重；当渗透率级差大于4.00 时，大裂缝分流量大于0.90，小裂缝分流量已经很小；且当大裂缝分流量大于0.90 时，渗透率级差与大裂缝分流量之间呈现出近似线性关系，由此可得到裂缝性岩心渗透率级差与大裂缝分流量的关系式，即裂缝渗透率级差界限预测公式：

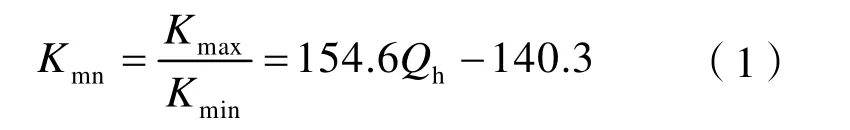
式中：Kmn为渗透率级差；Kmax为大裂缝渗透率，10-3μm2； Kmin为小裂缝渗透率，10-3μm2； Qh为大裂缝分流量。

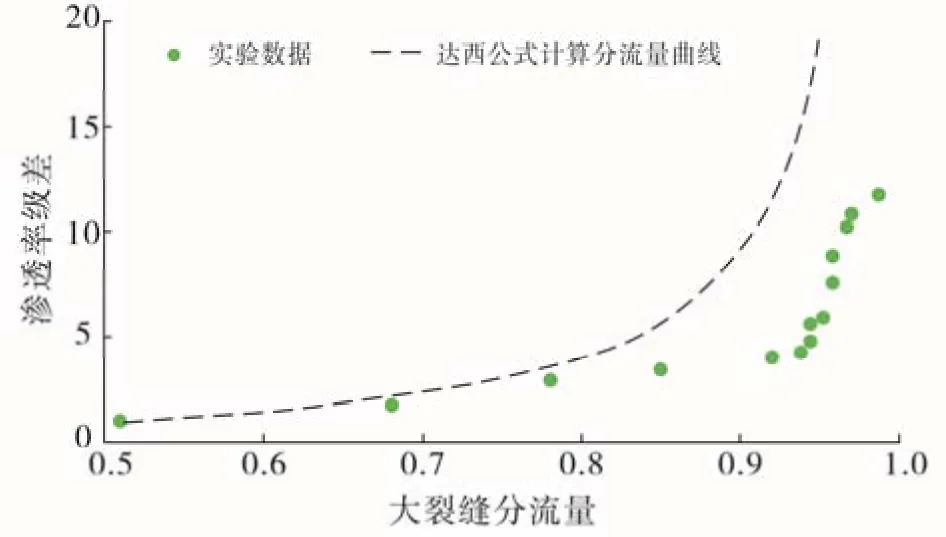
图2 缝间干扰实验和达西公式计算的不同渗透率级差的大裂缝分流量曲线

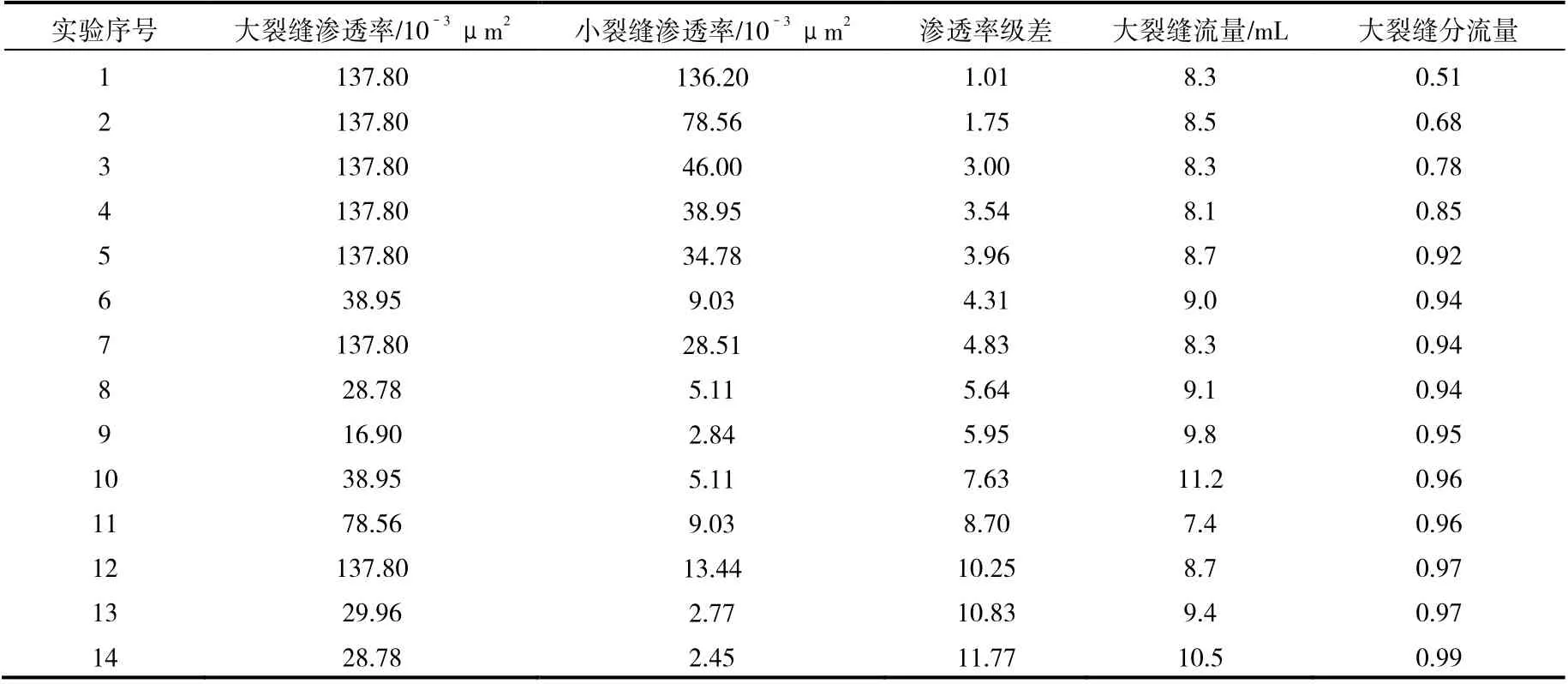
表1 实验数据统计

依据式（1）可知，当大裂缝分流量为1.00 时，渗透率级差为 14.30；当渗透率级差大于或等于14.30 时，在裂缝干扰效应的影响下，只有大裂缝参与渗流，小裂缝不参与渗流，即小裂缝没有液体产出；反之则当渗透率级差小于14.30 时，大裂缝与小裂缝均参与渗流。

2 理论分析

2.1 缝间干扰理论模型建立

图3 为缝间干扰理论模型示意图，其中，图3a为两层合采，图3b 为两层分采。

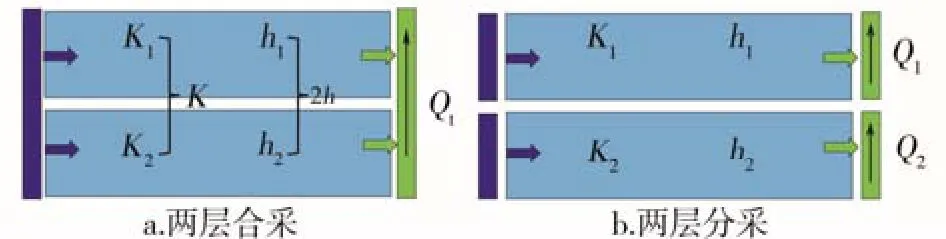
图3 缝间干扰理论模型示意图

假设两层合采时平均渗透率为K，厚度为2h，根据达西定律，产油量和产水量分别为：

式中：Q1t为大裂缝产液量，m3/d；Q1o为大裂缝产油量，m3/d；Q1w为大裂缝产水量，m3/d； K1为大裂缝渗透率，10-3μm2；K2为小裂缝渗透率，10-3μm2；h1为大裂缝有效厚度，m；K1ro为大裂缝油相相对渗透率； K1rw大裂缝水相相对渗透率。

上式中水相相对渗透率取值是通过油水相对渗透率曲线，根据不同裂缝含水上升速度快慢程度采用等间距原则进行选取。单采低渗透即小裂缝含水上升速度最慢，选取含水饱和度为 0.5 时的水相相对渗透率；单采高渗透即大裂缝含水上升速度最快，选取含水饱和度为 0.7 时的水相相对渗透率；合采时选取含水饱和度为 0.6 时的水相相对渗透率，如图4 所示。

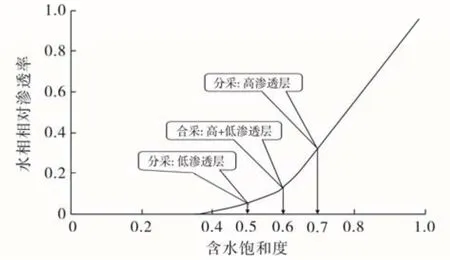
图4 不同裂缝水相相对渗透率选取

运用达西定律计算时可能存在如式（6）的情况，即合采时的产液量等于或小于分采时的高渗透层产液量，分析原因认为合采时缝间干扰致使低渗透层几乎不出液。

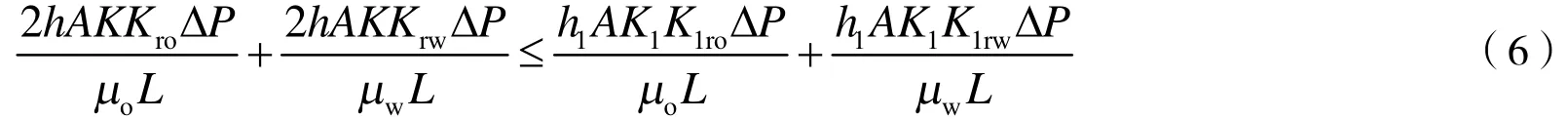
简化可得：

2.2 理论模型分析

实验中油水黏度比约为 3.04，油相水相渗透率比值约为 4.55，则 B=13.83，代入式（9）得 α ≥16.70，即渗透率级差大于16.70 时，低渗透层几乎不出液，与实验所得的渗透率级差结果（14.30）基本一致；同时，采取极限假设的思想，取 B=0，则α ≥2.40。即当渗透率级差大于2.40 时，高渗透层与低渗透层的分流量不再按渗透率比值进行分配，高渗透层与低渗透层间已具有较强的干扰作用（图2、图5）。

3 数模验证

为了验证实验结果，应用PETREL 软件建立3种不同渗透率级差的地质模型，并转化为ECLIPSE能够运行的油藏模型：网格数为80×20×15，网格步长为25 m×25 m×2 m，井距为400 m。地下原油黏度为 3.0 mPa·s，地层水黏度为 0.5 mPa·s，相对渗透率曲线及PVT 等参数则选取油田实测值。图 6 为含水率为 80%时不同渗透率级差条件下的油藏含油饱和度剖面，可以看出随着渗透率级差增大，干扰现象越来越明显，当渗透率级差为16.00时，基本为大裂缝产液，与室内实验和理论分析结果基本一致。

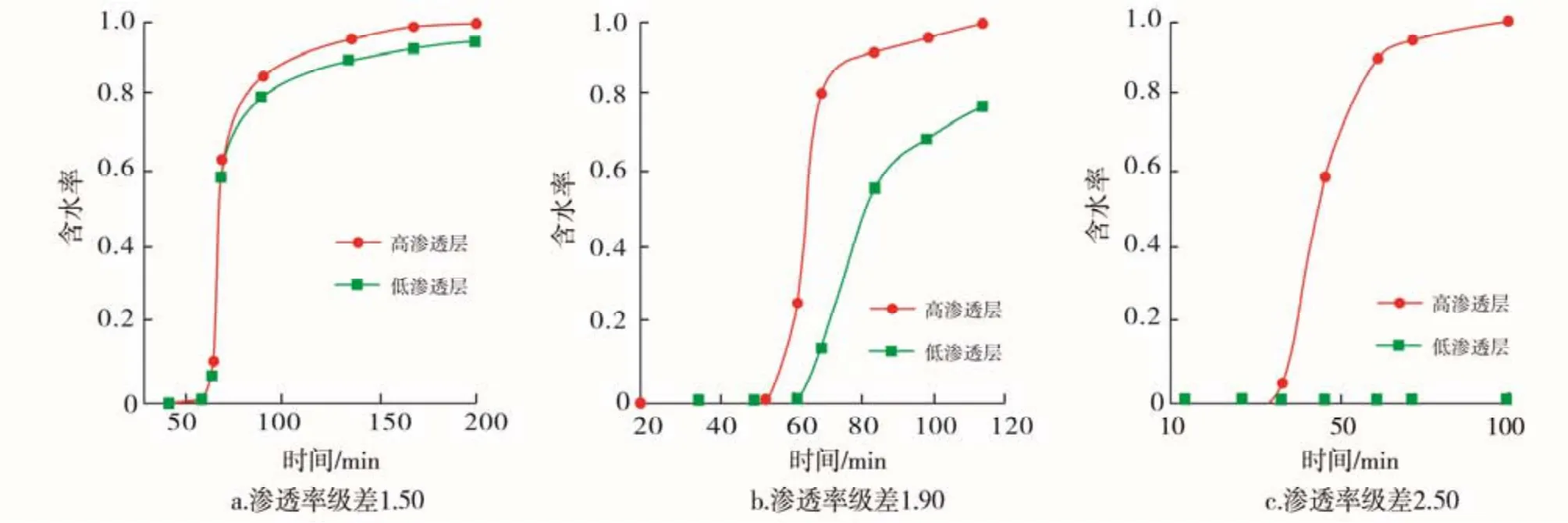
图5 不同渗透率级差模型储层含水率变化曲线（据白振强）

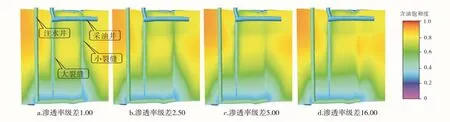
图6 含水率为80%时不同渗透率级差条件下油藏含油饱和度剖面

4 结论

（1）室内实验和理论分析表明，裂缝间渗透率级差大于2.40 时，缝间干扰产生，渗透率级差越大，干扰越明显，流量不再按达西定律分配。

（2）JZS 裂缝性油藏当渗透率级差大于 14.30时，由于裂缝干扰效应的影响，只有大裂缝参与渗流，小裂缝不参与渗流，即缝间干扰的渗透率级差界限为14.30。