福建省海陆复合系统协同发展研究
黄文彬 方 浩
(福州大学经济与管理学院, 福建福州 350108)
一、前言
福建省位处我国东南沿海地区,与宝岛台湾隔海相望,区位优势明显。为落实党的十九大关于“坚持海陆统筹,加快建设海洋强国”决策部署,促进海洋经济高质量发展,国家支持建设福州海洋经济发展示范区。面临全面深化改革带来的发展机遇,福建省海洋经济的发展恰逢其时。[1]目前福建省海洋经济发展存在海洋经济产业结构待优化、海洋经济领域的科研水平较低、生态环境污染等问题,这些因素限制了海洋经济的可持续发展。完善海陆统筹发展机制,实现海陆经济的互动与互补,是福建省建设海洋强省的新出路。
为了评价我国海洋经济与陆域经济协同发展情况,有学者进行了相关研究。范斐利用协同学理论解释了海陆经济之间的关系,并运用有序度模型和协同演化模型对辽宁省海陆经济的协同发展状况进行研究。[2]赵昕从系统理论出发,测度了我国海陆经济的耦合协调度及海陆经济系统关联度。[3]盖美运用DEA模型对海陆经济的相对效率进行测度,并在此基础上测算辽宁省海陆经济协调度。[4]赵梁从海陆统筹的角度出发,以沿海11个省市的面板数据为基础,计算我国2001-2013年沿海各省市海陆产业协调度。[5]综上可知,目前对于海陆协同发展的研究,大都集中于对样本数据时期内海陆协同发展水平的评价,缺乏对未来的前瞻性研究,预测性较差。同时,也未涉及对海陆协同发展进行调控的实证研究,后续研究意义薄弱。鉴于此,本文利用协同学理论[6][7],从部分、整体两个方面评价福建省海陆协同发展水平,并对未来海陆协同度进行预测,指出相应的调控措施,为福建省海陆协同发展提供合理建议。
二、海陆复合系统协同发展分析
(一)海陆复合系统有序度模型
复合系统[8][9]中的每一个子系统均由一定数量的序参量组成,序参量决定着子系统的演化过程。[10]设海陆统筹视角下海陆复合系统由海洋子系统与陆域子系统Si构成,i∈[1,2]。海陆复合系统的序参量Ei=(ei1,ei2,…,eim),eij为第i个子系统序参量的第j个指标,其具体数值为xij,βij≤xij≤αij,βij为指标eij的最小值,αij为指标eij的最大值,j∈[1,m]。若eij的值越大,子系统Si的有序度[11]越高,那么eij为效益型指标;若eij的值越大,子系统Si的有序度越低,则eij为成本型指标。海洋子系统和陆域子系统中各序参量分量的有序度可以表示为:
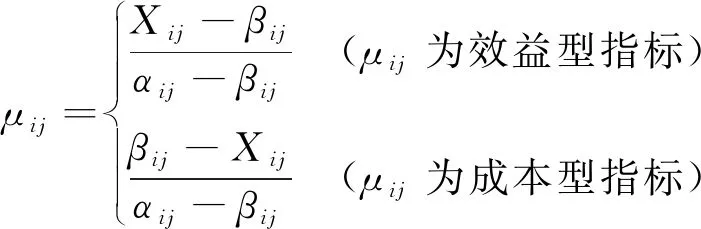
(1)
以上构造的序参量分量有序度取值在0到1之间,即0≤μij≤1,μij的大小代表了指标eij对子系统有序度的贡献的大小,μij的值越大,说明指标eij对系统有序度的贡献越大。子系统Si的有序度可以通过集成方法计算,目前,主要存在几何平均法和线性加权法两种集成方法。线性加权法通过不同的权数λij来考虑序参量各分量有序度在数值大小以及受重视程度上的差异,将序参量各分量有序度集成为单个有序度值,使得子系统有序度计算问题转化为一般性的线性规划类问题,更利于对有序度进行比较,因此本文选用线性加权法进行有序度的集成[12],具体公式如下:
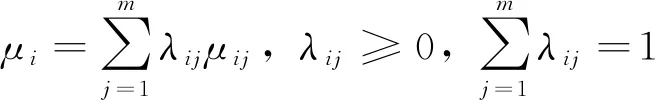
(2)
上式中μi为子系统Si的有序度;λij为各序参量的权数,代表着相应的指标eij在系统的有序发展过程中的重要程度。
(二)海陆复合系统协同度模型
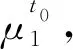
(3)
其中:

(4)
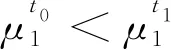
海陆复合系统协同度C具有如下特征:
(1)当C∈[0,1]时,说明海陆复合系统是协同发展的,C的值越大,则说明海陆复合系统的协同程度越高,反之,则说明系统的协同程度越低;
(2)当C∈[-1,0]时,说明两个子系统的有序度在t0到t1这段时间都有所下降,或者其中一个子系统的有序度提升,另一个子系统的有序度下降,从而导致海陆复合系统不能协同发展。
在公式(3)的基础上,分别计算海洋子系统与陆域子系统对海陆复合系统协同度的贡献度[14],当η=1时,海洋子系统贡献度u1与陆域子系统贡献度u2可以表示为:
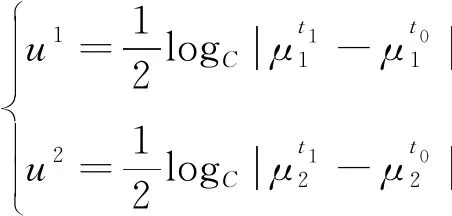
(5)
海洋子系统贡献度u1与陆域子系统贡献度u2分别表示海陆复合系统协同度有多大程度上由海洋子系统与陆域子系统决定,其中,u1+u2=1。
(三)海陆复合系统协同发展实证分析
1. 序参量指标的确定
为了分析海陆复合系统的协同关系,并根据客观性、系统性和有效实用性原则,分别构建海洋子系统与陆域子系统的序参量指标体系,其中海洋子系统与陆域子系统各28个序参量指标。
海洋子系统与陆域子系统均含有资源环境、社会经济、科学教育这3个一级指标。海洋子系统资源环境下二级指标为海水养殖面积(公顷)、海盐盐田总面积(公顷)、规模以上港口生产用码头长度(米)、沿海地区星级饭店客房数(间)、沿海地区旅行社总数(家)、海洋类自然保护区面积(平方千米)、工业废水直接入海量(万吨)、风暴潮灾害经济损失(亿元);海洋子系统社会经济下二级指标为海洋生产总值(亿元)、海洋生产总值占GDP比重(%)、海洋第三产业生产总值占比(%)、海洋经济劳动生产率、涉海就业人数(万人)、海洋捕捞产量(吨)、海水养殖产量(吨)、海洋矿业产量(万吨)、海盐产量(万吨)、海洋化工产品产量(吨)、造船完工量(万综合吨)、港口集装箱吞吐量(万吨)、国内旅游收入(亿元)、国际旅游外汇收入(万美元)、台站个数(个);海洋子系统科学教育下二级指标为开设海洋专业高等学校教职工数(人)、海洋专业专科及以上学历在校学生数(人)、海洋科研机构经费收入总额(千元)、海洋科研机构科技活动人员(人)、海洋科研机构科技专利授权数(个)。海洋子系统序参量指标中工业废水直接入海量(万吨)、风暴潮灾害经济损失(亿元)为成本型指标,其他均为效益型指标。
陆域子系统资源环境下二级指标为工业废水排放量(万吨)、工业废气排放总量(亿标立方米)、工业固体废物倾倒丢弃量(万吨)、铁路营业长度(公里)、公路通车里程(公里)、农作物播种面积(千公顷)、工业污染治理投资(亿元);陆域子系统社会经济下二级指标为陆域生产总值(亿元)、陆域生产总值占GDP比重(%)、陆域第三产业生产总值占比(%)、陆域就业人数(万人)、陆域劳动生产率(元/人)、全社会固定资产投资额(亿元)、农业产值(亿元)、能源生产总量(万吨标准煤)、工业产值(亿元)、建筑业总产值(亿元)、邮电业务总量(亿元)、旅客周转量(亿人公里)、货物周转量(亿吨公里)、社会消费品零售总额(亿元)、金融机构人民币各项存款(亿元)、进出口总额(万美元);陆域子系统科学教育下二级指标为普通高等学校专任教师数(人)、普通高等学校在校学生数(万人)、研究与试验发展经费内部支出(亿元)、科技活动人员(人)、专利授权数(个)。陆域子系统序参量指标中工业废水排放量(万吨)、工业废气排放总量(亿标立方米)、工业固体废物倾倒丢弃量(万吨)为成本型指标,其他均为效益型指标。
2. 序参量指标数据预处理与赋权
本文采用的数据预处理方法为归一化处理[15],将数据统一映射到[0,1]区间上,这样既可以去除数据的量纲差异,也可以提高模型的精度。同时,本文采用客观赋权法类的熵权法[16]对归一化之后的指标数据进行赋权。
3. 海陆复合系统有序度、协同度的计算与分析
根据海洋子系统与陆域子系统各序参量的性质,找出其所有年份中的最大最小值,并以最大值为上限,最小值为下限,将其代入公式(1)中,可以得到海洋子系统与陆域子系统序参量各分量的有序度,将序参量各分量的有序度的数据代入公式(2),可以分别得到海洋子系统与陆域子系统的有序度,如图1所示。
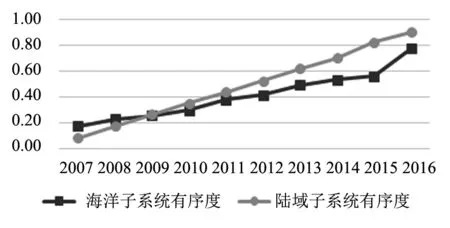
图1 2007-2016年福建省海洋子系统与陆域子系统有序度
从图1中可以看出,海洋子系统和陆域子系统的有序度从总体上来说是持续上升的,表明福建省海洋、陆域系统运行状态良好。其中海洋子系统有序度在2007-2009年大于陆域子系统有序度,在2009-2016年小于陆域子系统有序度,表明福建省陆域子系统有序度整体上高于海洋子系统有序度,福建省海陆经济的发展存在一定程度的不平衡。
将计算出的海洋子系统与陆域子系统有序度结果代入公式(3)与公式(5),即可得到海陆复合系统协同度与海洋子系统、陆域子系统对海陆复合系统协同程度的贡献度。其中,海陆复合系统协同度趋势变化如图2所示,海洋子系统和陆域子系统对海陆复合系统协同程度贡献度如图3所示。
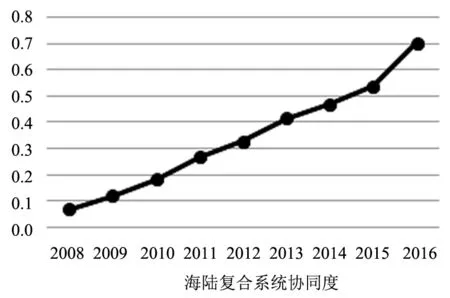
图2 福建省海陆复合系统协同度
由图2可知,福建省海陆复合系统的协同度逐年提高,由2008年的0.069上升到2016年的0.701,可见在海洋子系统与陆域子系统有序度稳步提高的基础上,福建省海陆复合系统的协同效应也随之增长。同时,由图3可知,海洋子系统对于海陆复合系统协同程度的贡献度也呈现增加的趋势,其贡献度始终保持的55%以上,并且在2016年达到了72%。这说明随着经济的发展,海洋子系统的经济规模虽然小于陆域子系统,但其重要性却与日俱增,在海陆复合系统的协同发展历程中扮演着重要的角色。
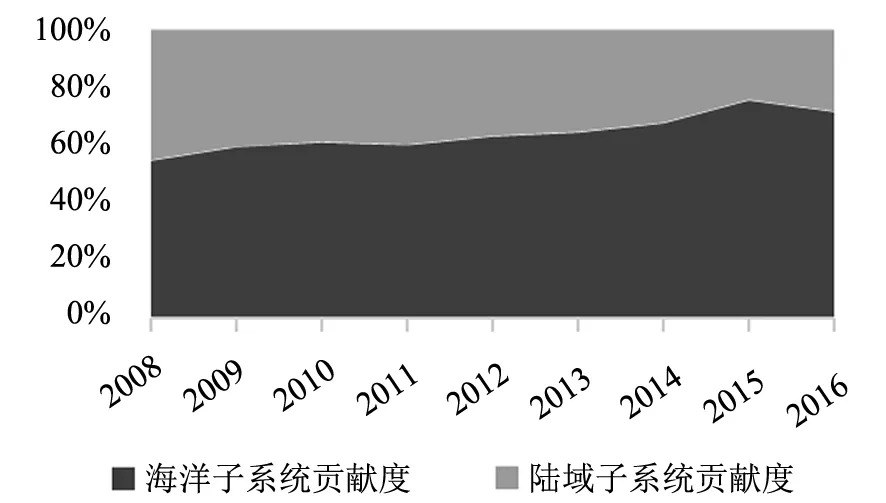
图3 福建省海洋子系统与陆域子系统贡献度
三、福建省海陆复合系统协同度的预测
本文运用BP神经网络模型[17]对海陆复合系统的协同度进行预测,从而对未来福建省海陆复合系统的发展状况有明确的认识,为海陆统筹视角下的海陆协同发展提供经济决策的实证支撑。
(一)BP神经网络原理介绍
神经网络的结构和算法有很多,其中BP神经网络是应用较为广泛的一种。BP神经网络是误差逆传网络的简称,是一种按照误差逆向传播算法训练的多层前馈网络。
BP神经网络的学习过程主要分为两个部分:
第一部分:训练样本从输入层传播至隐含层,再由隐含层输入至输出层,经过输出层的作用函数运算之后得到输出值。
第二部分:将第一部分得到的输出值与目标输出值相比较,看是否存在误差,若有误差,根据梯度下降学习算法,按照减小误差的方向,从输出层到隐含层逐层调整各节点的连接权值,直到输出值与目标输出值之间的误差在允许的误差范围之内,或者达到迭代次数上限为止。
(二)BP神经网络预测模型注意事项
1. 输入与输出数据样本
海陆复合系统协同度数据是一组时间序列数据,所以协同度数据既是预测模型的输入样本,也是期望输出。若假设海陆复合系统协同度序列为C(t),则输入样本序列为x(t)=(C1,C2,…,Ct-d),期望输出序列为do(t)=(C1+d,C2+d,…,Ct),其中d 2. 隐含层神经元的数量 当训练集数据确定之后,输入层和输出层的神经元个数也随之确定,接下来需要确定隐含层神经元个数。经过大量的实验证明,对于三层的神经网络,隐含层的神经元个数[18]可以选取: (6) 其中:a为1到10之间的常数,n和m分别为输入层和输出层的神经元个数。 1. 神经网络模型的训练 根据上文的分析,将样本数据与期望输出代入模型中,运用Matlab神经网络工具箱进行训练。[19]根据公式(3)可知,每一年的协同度均由本年度和上年度海洋子系统、陆域子系统的有序度计算而来,所以模型训练所用样本数据为2009-2016年系统协同度数据。设定预测值输出值与期望输出值误差为0.0001,神经网络最大迭代次数为1000次,经系统程序运行,在30次训练之后,神经网络的输出结果小于预设的误差阈值,结果如表1所示。从表1可以看出,神经网络模型训练所得结果与期望输出值之间误差较小,说明模型对样本数据的拟合精度较高。 表1 网络模型训练及误差 2. 预测及结果分析 通过训练后的神经网络模型预测海陆复合系统2017-2018年的协同度,结果如表2与图4所示。 从图4中可以看出,海陆复合系统协同度在2008-2018年呈现稳定上升的趋势,这说明,随着近年来福建省对海洋经济重视程度不断提高,并运用海陆统筹思想对海陆复合系统的发展做出战略规划,促成了海陆复合系统协同度的持续增长。2008-2016年,海陆复合系统协同度增长较为迅速,2017-2018年,海陆复合系统协同度的增长则趋于平缓。这一方面表明福建省海陆复合系统总体达到了较高的协同水平,充分发挥了海陆经济之间的协同作用;另一方面,则表明了福建省海陆复合系统的演化进入了较为平稳的阶段,在经历了10年的跃进式发展之后,需要继续对海陆复合系统内部的各项因素进行合理的调配,为下一阶段海陆统筹战略规划的实施夯实基础。 表2 海陆复合系统协同度预测值 图4 2008-2018年海陆复合系统协同度趋势 根据上文建立的海陆复合系统协同度预测模型,当系统协同度增长停滞或者下降时,需要在资源分配和战略规划上及时做出调整。海陆复合系统调节机制就是协调、控制海陆复合系统的运行,以保证其达到预期协同发展目标的功能体系。调控机制包括调控方法、调控模型和具体调控策略等部分。 1. 调控的方法 海陆复合系统是一个复杂的非线性系统,因此,对于这类复杂系统的调控可以使用非线性规划[20]方法,常用的非线性规划函数表达式如下: minf(x): (7) 其中:X=(x1,x2,…,xn)T∈En,表示X是n维欧氏空间En上的向量或点,X称为模型的决策向量,f(x),gi(X),hj(X)是定义在En上的实值函数,f(x)为目标函数,gi(i=1,2,…,m)、hj(j=1,2,…,l)均为约束函数,gi(X)≥0称为不等式约束,hj(X)=0称为等式约束。 2. 调控的主体与客体 海陆复合系统是复杂的巨系统,其调控的主体是政府,调控的客体是影响系统运行的相关要素。本文根据有序度评价模型,并结合调控的稳健性原则,选择有序度波动较大、有序度增长空间较大的子系统作为调控客体,有序度已经达到较高水平且较稳定的子系统作为参照,并随着被调控系统的变化而变化。子系统有序度波动性的大小采用熵值法[21]来确定,如公式(8)。 (8) 式中:μi为海洋子系统或陆域子系统在第i年的有序度。 3. 调控模型 (1)调控模型的目标函数 调控模型是针对海陆复合系统的协同度而建立的,所以,模型的目标函数为: minf=|Cμ-MCμ| (9) 式中:MC(μ)为预设的海陆复合系统协同度目标值,C(μ)为该年度协同度。目标函数的含义:海陆复合系统协同度的预测值与预设目标值之差最小。 (2)调控模型的约束条件 调控模型的约束条件包含以下几个方面:(1)μ1,μ2应满足协同度条件;(2)应符合最优发展模式,如果以海洋子系统为优先调控对象,则有约束条件μ1>μ2;反之,若以陆域子系统为优先调控对象,则有约束条件μ1<μ2;(3)根据海洋子系统与陆域子系统的有序度测算结果,2016年海洋子系统有序度为0.7740,陆域子系统有序度为0.9042,可见两个子系统有序度都已达到较高的水平,因此根据实际情况,令μ1,μ2≥0.6。 (3)调控模型的函数表达式 根据以上的约束条件,建立如下非线性规划模型: minf=|Cμ-MCμ| (10) 1. 调控对象的选择 根据表2中的协同度预测值,选择2018年作为调控目标年,该年度海陆复合系统的协同度为0.7521,与上一年相比涨幅较小,并且从整个考察时间段来看,增长率明显低于平均水平,需要进行调控。现假设将该年协同度调控为0.8以上,使系统达到高水平的协同发展状态。 根据目标函数公式minf=|Cμ-MCμ|,则有Cμ=MCμ≥0.8。 根据公式(8)的计算结果,得出海洋子系统和陆域子系统有序度的熵值分别为E(μ1)=0.9613,E(μ2)=0.9316,选择有序度波动较大的海洋子系统进行调控,陆域子系统的调整策略与之相适应。 2. 调控的过程 (1)在选定调控对象的前提下,根据调控模型的限制条件,即公式(10),分别计算出海洋子系统和陆域子系统的有序度变化临界值,得出海洋子系统有序度变化范围为0.8732≤μ1≤1,陆域子系统有序度变化范围为0.8595≤μ2≤1。 (2)根据约束条件公式,有0.6≤μ1,μ2≤1,在优先发展海洋系统的情况下,则有μ1≥μ2,由约束模型可以得出当μ2=μ1时,海陆子系统有序度均取值0.9306。此时,陆域子系统的取值范围则变为0.8595≤μ2≤0.9306,海洋子系统的取值范围变为0.9306≤μ1≤1。 3. 调控的结果分析 从以上的调控结果来看,福建省对于海陆复合系统的调控,重心应该放在对于海洋子系统的调控上,使得海洋子系统的有序度在0.9306以上,同时陆域子系统的有序度也要保持在0.8595-0.9306之间。结合上文的分析,可制定具体的调控措施如下: 在资源环境方面,减少各类工业废物的排放,加大对沿海港口码头的投资建设,完善省内交通物流网络,增加铁路、公路里程。出台扩大就业的引导政策,鼓励多层次、大范围的就业,增加就业人口。 在社会经济方面,扩大社会固定资产投资,促进社会消费,健全金融服务机制。针对不同产业出台相应的扶持政策,调整产业结构。加大对海洋产业就业的引导,鼓励多层次的劳动力进入海洋产业。重视文化产业建设,增加海洋第三产业产出。增加沿海观测台站数量,为海洋产业提供丰富准确的观测信息,为海洋经济的发展保驾护航。 在科学教育方面,既要加大科研经费的投入,产出更多对经济发展有益的成果,也要加快科技成果向实际应用的转化。以海洋新兴产业为导向,开展专题科技攻关工作,为未来海洋产业的升级打下坚实基础。扩大海洋类专业的招生规模,为海洋经济的发展输送大量高水平的人才,形成科研与经济发展的良性循环。 本文基于海陆统筹视角研究了海洋子系统与陆域子系统的之间的关系,选择海陆复合系统作为研究对象,结论如下:(1)2007年到2016年福建省海洋子系统与陆域子系统的有序度均保持上升的趋势,截至2016年,陆域子系统有序度更高,并且有序度的增长幅度也更大。但从增长率来看,海洋子系统有序度正处于高速增长时期,未来潜力巨大。(2)海陆复合系统协同度保持了较高的增长速度,并且海洋子系统有序度对于复合系统的协同度的贡献度逐年增高,未来海陆复合系统协同度的提高更多的在于海洋子系统有序度的增长。(3)经过对海陆复合系统协同度的预测,发现2017、2018年协同度增长放缓,尤其是2018年,海陆复合系统协同度与上年相比增长量仅为0.0071,单纯的系统自适应发展已经不能带来高速的协同度增长,需要政府利用多种手段对系统内可调控因素进行调控。(4)通过非线性规划模型对海陆复合系统的协同度、各子系统的有序度进行调控,发现若要实现2018年海陆复合系统协同度达到0.8的目标,应该优先对海洋子系统进行调控,并且海洋子系统有序度应该在0.9306以上,陆域子系统的有序度也应保持在0.8595到0.9306之间,在保证陆域子系统有序度波动不大的情况下,大力发展海洋子系统,提升其有序度。 注释: [1] 许嫣妮:《摸清海洋经济“家底”》,《福建日报》2017年6月1日,第4版。 [2] 范 斐、孙才志:《辽宁省海洋经济与陆域经济协同发展研究》,《地域研究与开发》2011年第2期。 [3] 赵 昕、南 旭、袁 顺:《巨系统视角下的海陆耦合协调机制研究》,《生态经济》2016年第8期。 [4] 盖 美、展亚荣:《辽宁沿海经济带海陆经济效率与协调性研究——基于DEA-Malmquist模型》,《资源开发与市场》2017年第6期。 [5] 赵 梁:《我国沿海省市海陆产业协调度分析》,《合作经济与科技》2018年第4期。 [6] 曹 峰:《“一带一路”背景下区域经济与港口协同——基于哈肯模型的实证分析》,《商业经济研究》2019年第14期。 [7] 徐海峰:《新型城镇化与流通业、旅游业耦合协调发展——基于协同理论的实证研究》,《商业研究》2019年第2期。 [8] 张树军、王光谦、杨 珏,等 :《复合系统理论在区域生态修复决策中的应用》,《清华大学学报》(自然科学版)2010年第12期。 [9] 殷林森:《基于复合系统理论的上海市科技经济系统协调发展研究》,《科技进步与对策》2010年第4期。 [10] 武淑萍、于宝琴:《电子商务与快递物流协同发展路径研究》,《管理评论》2016年第7期。 [11] 王银银:《中国海洋产业结构有序度研究》,《技术经济与管理研究》2017年第12期。 [12] 任 腾、陈晓春:《基于DEAHP模型的区域生态经济系统可持续发展评价》,《湖南大学学报》(自然科学版)2015年第3期。 [13] 汪明月、刘 宇、李梦明,等:《区域碳减排能力协同度评价模型构建与应用》,《系统工程理论与实践》2020年第2期。 [14] 金 雪、殷克东、张 栋:《中国陆海经济协同关系测度研究》,《中国渔业经济》2016年第1期。 [15] 张 戈:《课程推荐预测模型中的数据预处理方法研究》,《中国新通信》2019年第19期。 [16] 徐齐利:《熵权法综合评价系统设计与实现》,《软件》2020年第1期。 [17] 汤新程、王志海:《基于BP神经网络的房价预测研究——以邯郸市为例》,《统计学与应用》2019年第5期。 [18] 葛彩霞:《三层前馈型神经网络的最佳逼近研究》,《应用数学》1999年第1期。 [19] 李 奇:《Matlab智能算法工具箱在数据处理方面的应用》,《电脑编程技巧与维护》2018年第7期。 [20] 戴彧虹、刘新为:《线性与非线性规划算法与理论》,《运筹学学报》2014年第1期。 [21] 王富喜、毛爱华、李赫龙,等:《基于熵值法的山东省城镇化质量测度及空间差异分析》,《地理科学》2013年第11期。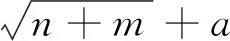
(三)BP神经网络预测模型实证分析


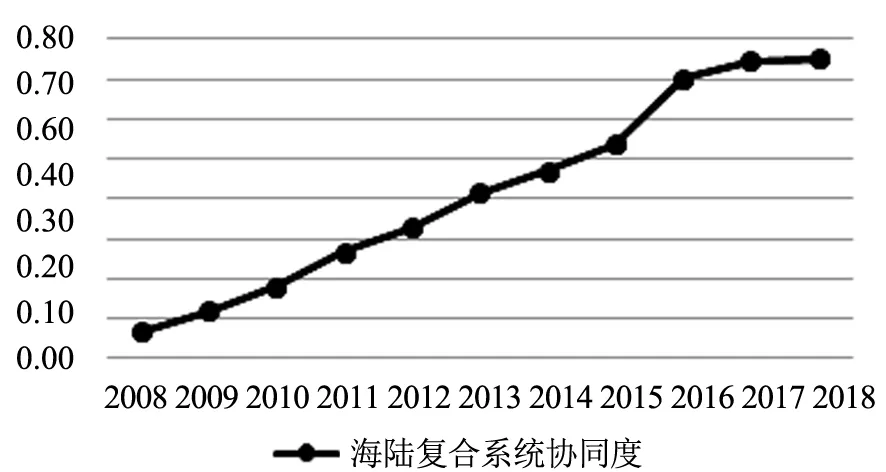
四、海陆复合系统协同发展调控
(一)海陆复合系统协同调控机制
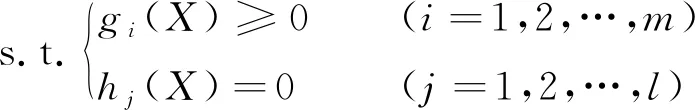
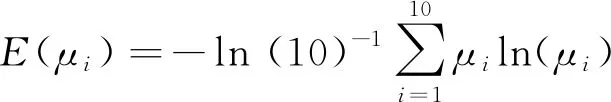
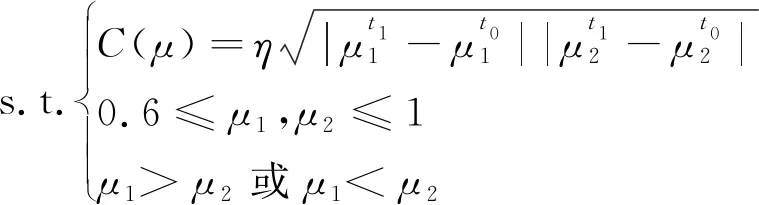
(二)海陆复合系统协同发展调控算例分析
五、结论

