定位焊点位置优化设计方法研究

刘纪 王地川 罗凤平 陆玉凯

摘 要：为了提高车身定位焊点选取的准确性，文章对焊点仿真建模的各项参数进行了灵敏度和相关性研究，给出了焊点参数对一阶模态影响因素的定量分析数据;采用hyperstudy及OptiStruct软件进行了定位焊点的位置选择方法研究，给出了在规定节拍下的多个零件组焊的最优焊点分布矩阵，结果表明：（1）焊点直径是影响一阶模态最重要的影响因素;（2）采用焊点离散优化设计的方法可以对定位焊点的选择提供设计依据。

关键词：定位焊点;Hyperstudy;焊点参数灵敏度;焊点参数相关性;有限元

中图分类号：TH706  文献标识码：A  文章编号：1671-7988（2020）21-62-04

Abstract： In order to improve the accuracy of GEO Welding Spot selection， the sensitivity and correlation of various parameters of Welding Spot simulation modeling are studied， and the quantitative analysis data of solder joint parameters to the first-order modal influence factors are given; the method of selecting the positioning solder joint is studied by using hyperstudy and Optistruct software， and the optimal solder joint distribution of multiple parts under specified beat is given The results show that： （1）Welding Spot diameter is the most important factor affecting the first-order mode; （2）The discrete optimization design method of Welding Spot can provide design basis for the selection of Welding Spot.

Keywords： Location solder joint; Hyperstudy; Solder joint parameter sensitivity; Solder joint parameter correlation; Finite element

CLC NO.： TH706  Document Code： A  Article ID： 1671-7988（2020）21-62-04

1 前言

點焊是汽车钣金件的主要连接方式之一，以其利于实现自动化机械化而被广泛采用。传统的点焊工艺布置多采用经验及对标的方法，且大规模采用机器人抓手进行工件搬运，由于节拍要求，定位焊点数量需要尽可能的降低，因此在后期试生产中需要不断优化焊点的位置，或需要增加机器人抓手的夹紧点，且很难评价定位焊点位置的优劣和对焊接尺寸精度的影响，笔者根据多年的经验提出了一种新的焊点位置离散优化的仿真方法，供大家探讨。

2 主流的焊点位置优化方法

现在行业内主流的焊点布置优化方法一般采用各向正交惩罚材料密度法，即SIMP，将有限元模型设计空间的每个单元的密度作为设计变量，该单元密度同结构的材料参数有关（单元密度与材料弹性模量E之间具有某种函数关系），0～1之间连续取值，优化求解后单元密度为1（或靠近1）表示该单元位置处的材料很重要，需要保留;单元密度为0（或靠近0）表示该单元处的材料不重要，可以去除，从而达到材料的高效率利用[1]。

但是该方法在焊点的拓扑优化中，以焊点的体积分数为设计变量，约束焊点的体积分数，以一阶固有频率最高为设计目标时，焊点由于惩罚系数的选择需要试算法，且很难全部实现焊点的0～1分布，优化不彻底，棋盘格现象较为严重，在此定义为焊点选取的软方法。本文提出了一种新的方法，记为焊点选取的硬方法，即强行将焊点进行0～1分布，实现焊点的离散仿真研究。

3 焊点模型的建立方法

目前对于白车身点焊的模拟，主要有3种类型。

（1）使用刚性梁单元对所焊接的面网格进行点对点连接。

（2）采用剪弹性两单元，如CWELD及CFSAT等。这种特殊的剪弹性梁单元，是通过Krichoff壳理论建立约束方程将所焊接单元连接，可以定义焊点直径。

（3）采用ACM2单元，这种类型焊点是先建立一个六面体块单元，然后将六面体通过RBE3单元与所焊接的2层网格进行连接[2]。

Cweld焊点单元不仅可以实现点对点连接，而且还可以实现点对面、面对面连接，对网格的协调性要求较低，对于通常具有4000-6000个焊点的白车身来说，建模效率高，使用很广泛，本文以cweld焊点为研究对象，对定位焊点位置布置进行研究。

4 焊点参数对一阶模态响应的灵敏度分析

焊装生产线中的工况较少，一般为重力场下的柔度及生产线和机器人的振动，因为获取生产线及机器人的振动频谱较为困难，本文采用零件在约束条件下的一阶模态进行了简化分析，不考虑重力场，以一阶模态最高为分析目标。

前文所述，采用SIMP的方法优化焊点数量，由于惩罚系数的选择较为困难，为了解决此问题，本文采用了Hyper -study多目标优化分析软件进行了研究。

4.1 cweld焊点对模态的相关性及灵敏度研究

Cweld焊点包含弹性模量、泊松比、密度及焊点直径等主要参数，为了识别出分析的设计变量，首先需要对其各个参数进行对一阶模态的灵敏度分析，研究采用的网格尺寸为10mm，焊点直径选择为6，弹性模量E为210000MPa，泊松比0.3，密度7.85E-9mm3/t。

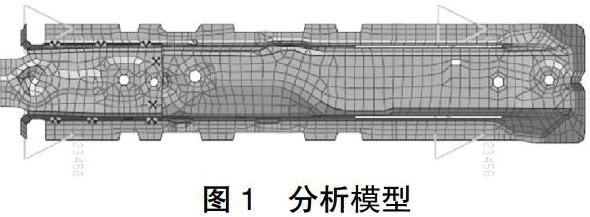
分析模型如图1，为某车型的座椅横梁，边界条件为限制标记位置节点的6自由度，求解该模型的一阶模态。

使用Optistruct模板，hypermesh软件建立零件的分析模型，使用hyperstudy软件分别以焊点直径、弹性模量、泊松比、焊点密度为设计变量，各选取10组数据，以一阶模态作为响应，寻找焊点各参数与一阶模态的相关性及灵敏度。

相关性，是指两个变量的关联程度。一般地，从散点图上可以观察到两个变量有以下三种关系之一：两变量正相关、负相关、不相关。如果一个变量高的值对应于另一个变量高的值，相似地，低的值对应低的值，那么这两个变量正相关[3]。

灵敏度（Sensitivity）是指某方法对单位浓度或单位量待测物质变化所致的响应量变化程度，它可以用仪器的响应量或其他指示量与对应的待测物质的浓度或量之比来描述。

（1）杨氏模量对一阶模态的灵敏度，相关系数为0.4，两者表现为正相关，如图2。

（2）泊松比对一阶模态的灵敏度分析，相关系数为-0.999，两者表现为负相关，如图3。

（3）密度对一阶模态的灵敏度分析，相关系数为0，两者表现为不相关，如图4。

（4）焊点直径对一阶模态的灵敏度分析，相关系数为0.8，两者表现为正相关，如图5。

通过对比：

1）弹性模量在下降到0.1MPa后，一阶模态仍为19.44hz，灵敏度表现不良，相关性也较低;

2）泊松比与一阶模态的相关性强负相关，但灵敏度表现较差，下降5个量级几乎未影响一阶模态的变化;

3）密度的变化对一阶模态无影响;

4）焊点直径与一阶模态为正相关，正相关性最大，在焊点直径下降4个以后，一阶模态下降最多，灵敏度最高。

由上，为了降低设计变量对一阶模态的扰动，本次的研究分析以焊点直径为研究对象，分别建立最少化定位焊点及最大化一阶模态的优化目标。

由于定位焊点是总体焊点中的一部分，因此下文以单个焊点为研究对象，由上文得出焊点直径在下降到1e-6后，一阶频率下降了约400倍，因此本文认为焊点直径为1E-6时焊点为取消状态，直径为6时取为定位焊点。

由上文，优化设计三要素设计变量、约束条件、目标函数，文中已定义完成设计变量和目标函数，将每个焊点分别单独研究，还需要建立一种关联定位焊点与总体焊点之间的数学关系，来建立约束约束条件。

由图5得出，一阶模态与焊点直径成某种正比关系，式中g（x）为一阶模态，x为焊点直径，β为比例系数，如公式（1）：

由数学原理得出，一阶模态与焊点直径之和也成某种正比关系，式中g（x）为一阶模态，x为焊点直径，α、β为比例系数，如公式（2）：

因此将焊点直径之和做为设计的约束条件是成立的。

5 定位焊点布置优化研究

5.1 模型的建立

分析模型为某在产车型的前围板总成，共有90个焊点，12个零件，采用Hypermesh建模，焊点采用CWELD建模，边界条件设置为图示位置的6自由度约束，见图6。以每个焊点的直径为设计变量，焊点直径之和为约束条件，一阶频率为设计目标。

建立频率分析工况，提取前6阶的固有频率。

通过前述的分析，焊点直径标称为6，最小取值为1e-6。

建立优化设计的数学模型，如公式3：

式中，X为每个焊点的直径，f（xj）为焊点直径之和，g（xj）为一阶模态。

在Hyperstudy下运行System Bounds Check，模型的一阶频率分别为为20.54HZ，0.29HZ，模态之比为70，灵敏度良好，焊点直径之和分别为540，9.00e-05。

5.2 优化设计-识别最优的焊点分布

对模型进行优化设计分析，识别最优的焊点分布，采用全局搜索优化方法，建立最少化焊点直径之和及最大化一阶固有频率的分析目标，作业总数为200次。

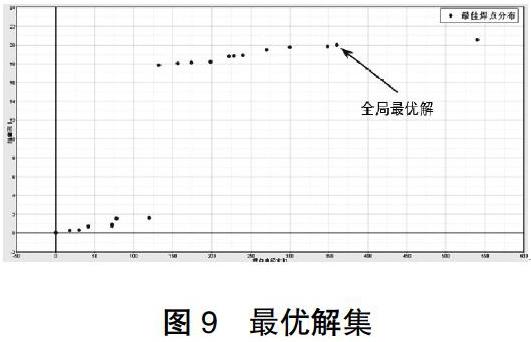
由最优解集可以得出，焊点直径之和与一阶固有频率程近似正比函数，与图5曲线相近，表明以焊点直径之和为约束条件是成立的。

随着焊點数量的增多，一阶模态不断提高，最优的焊点直径之和为360.00003，即焊点数量为60个，一阶模态为20.01HZ，相较初始模型的20.54HZ，下降0.53HZ，焊点数量减少了30个。

迭代历程如图7，迭代图见图8。

最优解集如图9。

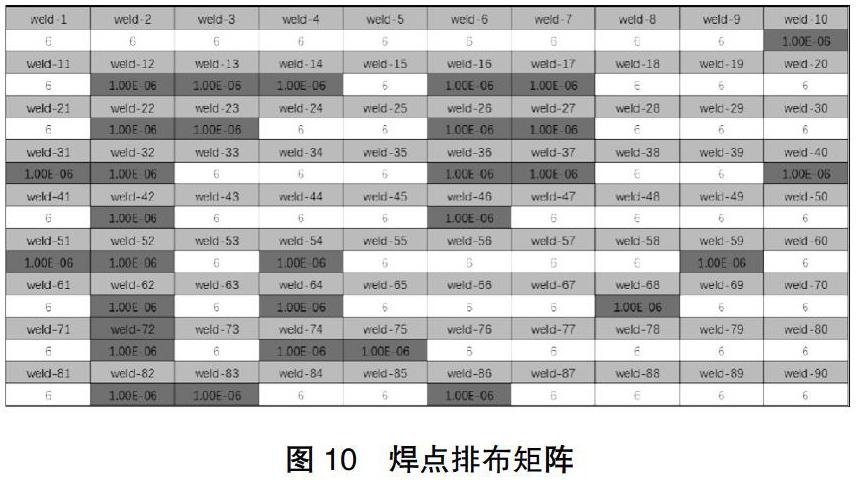
最优焊点排布矩阵如图10，其中红色表示可以删除的焊点标号。

通过最优解图9，为了满足一阶频率最高并结合目前生产线的节拍要求的可以焊接38点的设计目标，得出最优解：

（1）f（x）≤228，即38个焊点，如下图11所示。

（2）一阶模态18.82HZ。

工艺最优解焊点排列矩阵如图12。

导入hyperstudy分析结果目录下的相应计算文件后的焊点位置分布，图13：

一阶模态为18.82HZ，即在当前工艺设计下的最优焊点分布，最终焊点分布模态云图，如图14。

对比初始焊点分布，焊点数量减少52个，模态降低1.72HZ。

6 结论

本文结合hyperstudy及optistruct，对焊点各项参数的灵敏度进行了分析，得出了焊点各建模仿真参数对一阶模态的灵敏度。通过多目标优化分析得出了在给的焊点数量前提下一阶模态最高的定位焊点布置位置，为焊接工艺的选择提供了设计依据：

（1）焊点直径是影响一阶模态最重要的影响因素;

（2）采用焊点离散优化设计的方法可以对定位焊点的位置选择提供设计依据。

参考文献

[1] 洪清泉，赵康，张攀.OptiStrucs & HyperStudy理论基础与工程应用[M].机械工业出版社， 2013.

[2] 王力.汽车车身CAE分析中焊点模型的易用性[J].汽车工程师， 2014 （2）： 19-22.

[3] 周健民，沈仁芳.土壤学大辞典[M].科学出版社，2013.

[4] 母德强，杨君.MM52160龙门导轨磨床立柱的拓扑优化[J].机械工程师， 2014（2）：61-64.

[5] 刘甚宏，关英俊，张力锋等. GMCU2060龙门加工中心横梁的结构优化设计[J].机械工程师，2014， 000（002）：97-99.

[6] 刘甚宏，关英俊，张力锋等.XK2423数控铣床立柱的有限元分析与拓扑优化[J].组合机床与自动化加工技术，2014，000（008）：22-25.