维修加固桥梁的抗震韧性评价方法

俎林 黄勇

摘要：以《公路桥梁技术状况评定标准》（JTG/T H21—2011）中的跨中挠度限度为损伤指标来进行主梁的易损性分析，提出了一种针对维修加固桥梁的抗震韧性评价方法。以一座在多年运营发生破坏后进行过主梁维修加固的五跨连续梁桥为例，采用有限元建模和模型修正的方法，利用增量动力分析，研究了维修加固前后桥梁的主梁构件在不同强度地震作用下易损性的变化;利用经验统计方法探讨了既有桥梁弹性模量与跨中挠度的关系，提出了基于跨中挠度的功能损失函数;结合案例桥梁具体维修加固工法，初步建立了恢复函数曲线，计算了维修加固前后桥梁的抗震韧性指标。分析结果表明：针对维修加固桥梁，利用跨中挠度作为损伤指标进行抗震韧性评估是可行的，从易损性曲线可以得到维修加固对于抗震性能的提升是较为明显的;维修加固对于韧性提升是随着破坏等级的提升递减的，对轻微破坏较为明显，至结构失效时则差异较小。

关键词：桥梁易损性;跨中挠度;损伤指标;连续梁桥;增量动力分析

0 引言

近年来，地震工程界的抗震设计理念开始从单一强调地震安全性向安全性与可恢复性并举方向转变。2017年，在智利举行的16届世界地震工程大会就已提出“韧性，地震工程的下一个挑战”的口号（黄勇等，2017），同时，“韧性城乡”也是中国地震局提出的四大科学计划之一。

Bruneau等（2003，2007）提出了可恢复性的概念，并将其应用于研究急诊医疗部门的运行和物理可恢复性，且把概率函数、易损性、可恢复性联系起来;Chang和Shinozuka（2004）提出了社区可恢复性的研究框架，用不同地震动强度下功能损失的累计超越概率作为可恢复性指标;Manyena（2006）梳理了可恢复性的概念，将抗震可恢复性定义为：系统、社区或社会在遭受预设的干扰下通过改变它的非必要属性来适应、生存并自我修复的内在能力;Cimellaro等（2007，2010，2016）在抗震可恢复性的定量研究上做了进一步工作，提出了地震可恢复性指标，并且提出了一种形似单自由度有阻尼自由振动方程的非线性恢复函数;Renschler等（2010）提出了新的可恢复性研究框架，由2003年的4个维度扩充重组成了7个维度，即人口、环境、组织、物理基建、生活方式、经济、社会文化;Alberto等（2013）提出一个震前预测桥梁可恢复性的概率方法，利用基于6参数三角函数的功能函数描述桥梁的时变功能，根据区域风险确定性态水准和恢复策略;Ashok和Swagata（2014）通过易损性分析、建立损失函数、恢复模型计算一座公路桥梁的可恢复性指标，并通过与抗震加固后可恢复性指标的变化来分析加固的效果。

当前，桥梁的易损性分析和抗震韧性评价大多将关注点集中于桥墩、支座等的抗震性能上，而许多因服务年限进行维修加固的桥梁，主梁的刚度变化才是其加固前后需要关注的主要特点。关于如何评价此类桥梁维修加固后的抗震韧性，目前研究较少。本文以一座在多年运营发生破坏后进行了主梁维修加固的五跨连续梁桥——嫩江东桥为例，提出了一种以跨中挠度为指标的适用于维修加固桥梁的抗震韧性评价方法。

1 维修加固桥梁地震易损性分析

1.1 研究桥梁选取

本文选择齐齐哈尔嫩江东桥为研究对象，该桥梁位于齐齐哈尔市梅里斯达斡尔族区，是齐齐哈尔与西北部各市、县的重要交通要道。嫩江东桥主桥上部结构采用预应力混凝土连续箱梁，跨径布置如图1所示。该桥于1991年10月开工建设，1995年竣工，至今已经运营了25年，在2017年的桥梁检测中发现主桥各中跨发生了较为严重的下挠，箱梁也出现了结构性与非结构性的裂缝。动载试验显示，主桥基频下降，车辆行驶过程中会产生较大的振幅，冲击系数超出了设计值。在维修加固主梁中采用以主动加固为主，被动加固为辅的方法，主动加固采用体外预应力法，被动加固采用增大截面法和粘贴钢板法。

1.1.1 有限元模型

根据相关设计资料确定有限元模型的相关参数为：主梁采用C50混凝土，弹性模量为3.5×104 MPa，泊松比为0.2;桥墩采用C40混凝土，弹性模量为3.3×104 MPa，泊松比为0.2;桩基采用C30混凝土，弹性模量为3.0×104 MPa，泊松比为0.2;纵向预应力筋为高强低松弛钢绞线，标准强度为1 860 MPa，弹性模量为1.9×105 MPa;体外预应力束均采用6束钢束，控制张拉应力为1 209 MPa，纵向预应力筋与管道的摩擦系数k=0.3;支座采用30 000 kN的盆式橡胶支座，盆式橡胶支座的摩擦系数f=0.10。10#桥墩处盆式橡胶支座为固定支座，水平与竖向刚度设置为大刚度，其余支座为双向活动支座。根据《公路桥梁抗震设计细则》（JTG/TB02-01—2008），得到支座刚度输入模型，进而计算得到水平力大于活动盆式支座的临界摩擦力，为了简化计算，将活动支座水平刚度设为0。桩基根据Matlock法计算，利用节点弹性支承模拟土弹簧，同一土层分成若干部分，将每一个部分看成一个弹性支承，位置作用于其合力点。计算桩端地基竖向抗力系数时，深度不足10 m时，取值为10。根据地质勘测报告得到，主河槽平均分布厚30 m的砂砾层以及36 m的厚砾石层，交错分布，地基承载力较高。利用Midas/Civil建立的有限元模型如图2所示（葛俊颖，2013）。

1.1.2 分析阶段与振动模态

本文对3个阶段建立3个模型：第一阶段：桥梁建成完好状态，模型一阶频率为1.104 Hz，根据竣工后桥梁检测报告得到的一阶频率为1.0 Hz，所以该有限元模型较為准确。第二阶段：疲劳损伤状态，根据2017年有关机构的桥梁动载试验报告得到一阶频率为0.879 Hz，因为该桥梁基频的下降是综合因素（温度、裂缝的产生、预应力的损失等）作用的结果，为了方便模拟桥梁破坏状态，以降低主梁的弹性模量进行模拟桥梁刚度的下降，经过试算弹性模量由3.5×104 MPa降到1.9×104 MPa，一阶频率可达0.890 Hz，较为接近动载试验结果，可以该状态模拟桥梁破坏状态。第三阶段：维修加固结束阶段：对裂缝采用粘贴钢板进行处理，采用全截面进行计算，并且增大关键截面和增加体外预应力来模拟维修加固阶段。表1列出了3个阶段的自振频率，图3为桥梁前三阶振型图，3个阶段的有限元振型并未发生改变。

1.2 增量动力分析

增量动力分析（IDA）方法是通过对若干条地震动记录进行调幅，得到多组不同强度的地震动数据，同时输入三向地震动，对结构进行时程反应。

（1）地震动选取

齐齐哈尔市梅里斯达斡尔族区为Ⅱ类场地，峰值加速度（PGA） 为0.05 g，反应谱特征周期为0.35 s，抗震设防为Ⅵ度区。根据相关规范可知，阻尼比为0.05，桥梁重要性为B类，重要性系数为0.5，场地系数为1.0。根据以上参数设计反应谱，在太平洋地震工程中心（PEER）地震动数据库选择了20条地震动（表2），并进行归一化。

（2）IDA分析

利用Midas建立桥梁维修加固前后2个阶段的有限元模型，分别输入20组PGA为0.1，0.2，0.4，0.6，0.8和1.0 g的地震动，进行地震反应分析，得到不同地震强度等级下主跨跨中挠度的大小。

1.3 损伤水准划分

根据《公路桥梁技术状况评定标准》（JTG/T H21—2011）中梁式桥上部结构构件技术状况评定中关于跨中挠度的定量描述，设跨中最大挠度为δmax，计算跨径为L0。令损伤指标D=δmax/L0，每种标度对应的损伤指标范围见表3。

图4为破坏状态及维修加固状态的跨中截面能力与需求关系。从图4可知，随着PGA逐渐增大，桥梁逐渐发生破坏且破坏程度逐渐加大。在图4a 中，地震动2未使橋梁发生破坏，地震动1使桥梁发生轻微破坏而未产生严重破坏，其余地震动都使桥梁发生了结构失效。这一现象在地震动11～20作用下表现尤为明显，说明了这座桥在多年运营下发生破坏后，抗震性能下降较为明显。图4b显示，地震动1，2都未对桥梁产生破坏，与未进行维修主梁相比，发生各类型破坏所需要的PGA变大，可以看出维修加固后桥梁的抗震性能有明显提升。1.4 易损性分析 本文采用能力需求比方法，利用二次多项式进行方程拟合，通过IDA分析得到了发生各类损伤的需求值Sd与各损伤指标Sc，以ln （Sd/Sc）为纵坐标，ln （PGA）为横坐标进行回归分析，可以得到：

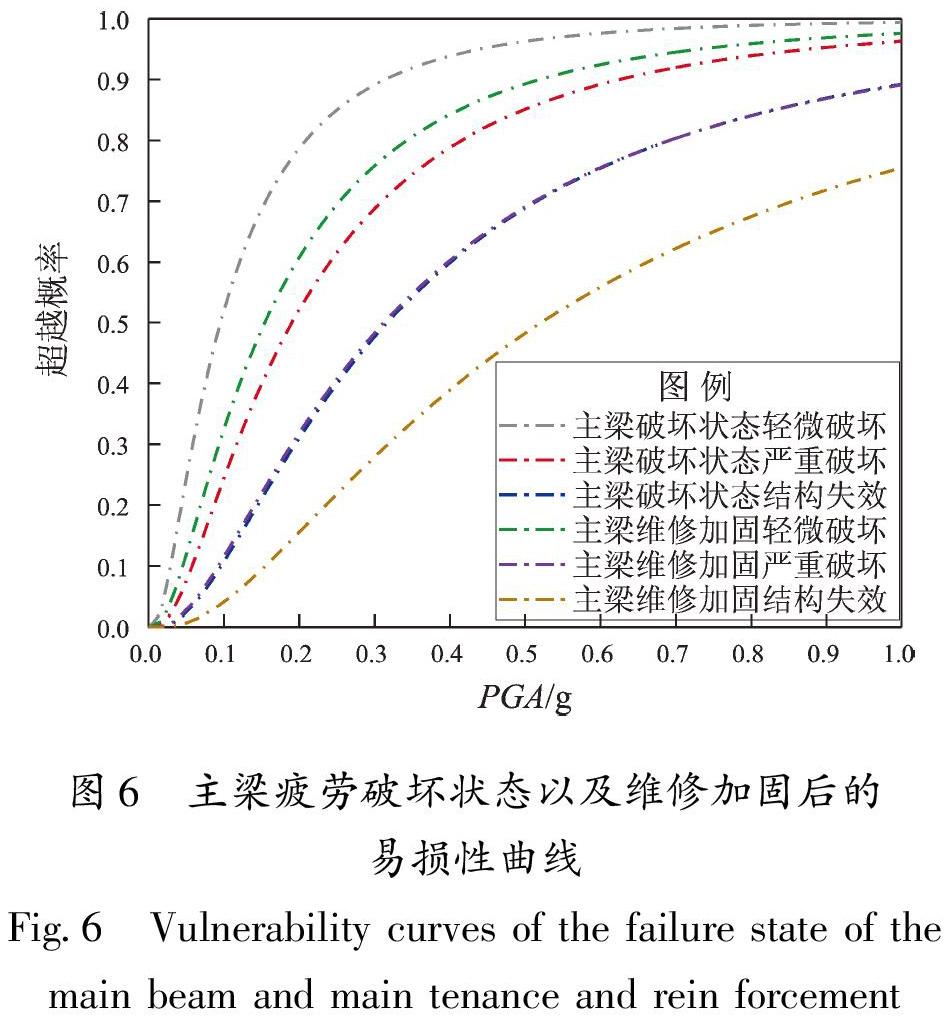
以主梁疲劳破坏状态中的轻微破坏为例，其二次拟合曲线如图5所示。通过计算，可以得到主梁疲劳破坏状态以及维修加固后的易损性曲线如图6所示。

由图6可见，随着PGA的增大，不同破坏类型的超越概率都逐渐提升。以PGA=0.2 g为例，在主梁疲劳破坏状态下发生轻微破坏的概率高达80%，经维修加固后概率下降到接近60%，抗震性能提高效果显著。相比于主梁疲劳破坏状态的易损性曲线，主梁维修加固后的易损性曲线整体发生了下移，这表明维修加固较大地提升了桥梁的抗震性能。

2 抗震韧性评价

抗震可恢复性评价指标（即韧性评价指标）是在易损性分析基础上，结合损失函数和恢复模型计算得到。本文中的损失函数分为两种情况：第一类指桥梁在实际运营中受到的损伤导致的功能损失;第二类指在不同地震作用下桥梁可能出现的功能损失。恢复模型是依据维修加固工法所需时间的特点确定。

2.1 损失函数

2.1.1 经验疲劳损伤估计方法

桥梁破坏很大程度源于疲劳损伤，越来越多的重载车辆从桥梁上频繁通过，对桥梁造成严重破坏，导致梁体的开裂。根据李秀芬等（1997）实验得出的桥梁在疲劳荷载下，高强混凝土的弯曲变形模量为混凝土受压弹性模量的0.875倍的结论，疲劳变形模量可表示为：

式中：Efb为疲劳变形模量;N为疲劳荷载作用次数;Ec为混凝土受压弹性模量。

由于缺乏嫩江东桥交通量的统计，笔者采用李世安（2009）使用的交通量得到的疲劳荷载作用次数的二倍进行计算（原文献中桥梁跨径小，全长为300.25 m，使用轻型交通进行计算，而嫩江东桥跨径较大并且为重要的跨江桥梁），根据疲劳荷载作用次数计算的出疲劳变形模量，为了模拟预应力损失将张拉预应力减小10%，利用短期效应组合计算跨中挠度，以上参数见表4。对弹性模量与跨中挠度利用Allometric模型进行曲线拟合，拟合曲线如图7所示，拟合公式为：

当弹性模量为1.9×104 MPa时，利用公式（3）计算挠度为65.23 mm，使用模型修正后的Midas有限元模型进行分析，计算挠度为60.71 mm，误差为7.4%。将式（3）代入疲劳变形模量公式得到：

利用式（4）可以大体估计出疲劳荷载在服务年限16年间造成桥梁跨中挠度增加和弹性模量变化的情况，此方法可用于没有详细桥检试验数据的桥梁损伤初步评估。

2.1.2 损失函数

地震中的损失包括两类，一类为直接损失，是瞬间发生的关于PGA的函数，另一类为间接损失，如经济损失等，本文不考虑间接损失。直接损失采用的计算公式为：

式中：LD为直接损失;k为桥梁的损伤状态;PE为发生概率;rk为损伤比，对应3类破坏状态轻微、严重、失效，本文rk分别取0.08，0.25，0.4。

一般来说，预应力钢筋混凝土连续梁桥主梁在地震作用下往往仍保持线弹性特点。本文利用式（2）进行数据拟合，得到以PGA为自变量的损失函数，损失函数分为破坏状态和维修加固后遭遇地震时的损失函数，拟合曲线如图8所示。

2.2 恢复函数

根据案例的桥梁维修加固方案，首先对裂缝粘贴钢板，然后施加体外预应力，最后对不满足新规范的截面进行腹板加厚，在张拉预应力筋采取按边跨—次边跨—中跨依次张拉的顺序来进行，一般需要32 d左右，见表5。

假定地震发生后的维修加固过程也是基本按照这一程序进行。地震后的恢复函数利用非线性微分方程来描述，由于该桥梁在运营期间已经发生破坏并且经过了维修加固，利用1.3节与2.1节得到的结论，假定在运营过程中功能下降到了65%，维修加固过程利用线性恢复函数计算。当破坏程度达到35%，此时对于该桥来讲已经到了一个阈值，必须进行桥梁的维修加固。在破坏状态下，假定使用功能下降到75%且可以正常运营，地震后的恢复函数为：

式中：L0为初始破坏程度，根据《地震现场工作（GB/T 18208.4—2011）》第四部分，轻微破坏程度为20%、严重破坏程度为50%、结构失效为100%;w对应于轻微破坏取0.2、严重破坏取0.1、结构失效取0.05。

假設恢复程度都可以达到99%，利用恢复函数与恢复程度可以确定修复时间，将该恢复时间与常规维修加固经验以及孙振凯和邹其嘉（1999）研究中的桥型、跨径与烈度确定的修复时间进行对比，确定疲劳损伤尚未维修情况下遭遇地震时3个阶段的恢复时间依次为28，66和136 d，维修加固后遭遇地震再次加固时修复时间分别是25，59和133 d，功能曲线如图9所示。

2.3 韧性评价指标

功能函数Q（t）描述的是一个非平稳的随机过程，是一个分段函数，对于地震后的恢复过程，功能函数与坐标轴围成的面积可以量化韧性，韧性可按下式进行计算，计算结果见表6。

韧性指数越大代表可恢复性能力越强。经过维修加固的桥梁比出现破坏但尚未维修的桥梁的韧性指数要大一些，说明常规维修可以使抗震恢复能力提高，也说明了无论从运营角度还是抗震角度来讲，对桥梁的定期检测和维修加固都是必要的。对于轻微破坏来讲，维修加固对其韧性的提升是十分明显的，但随着破坏程度的逐渐加大这种效果是逐渐递减的，当结构失效时，韧性提升水平已无多少差异。

3 结论

本文围绕一座在运营多年后产生破坏并进行了维修加固的连续梁桥，采用地震反应和地震易损性分析其破坏以及维修加固过程，得到以下结论：

（1）针对维修加固桥梁，利用增量动力分析（IDA）以跨中挠度与跨径的比值作为损伤指标，对桥梁破坏状态和维修加固后进行抗震韧性评估，这种方法是可行有效的。易损性分析计算得到的超越概率较大，这是因为损伤指标是基于跨中最大挠度与跨径的比值提出的，而这一指标在《公路桥梁技术状况评定标准》（JTG/T H21—2011）中是与行车通行紧密相连的，所以结构失效会影响行车安全，但并不会对结构本身发生坍塌落梁等情况，这也表明了该项损伤指标是较为敏感的。

（2）桥梁常规的维修加固（非抗震加固）可以较为明显地提高桥梁的抗震能力。在本文计算损伤函数的所使用的方法可以应用于无桥梁检测资料的桥梁，以便于进行桥梁韧性评估，当然这一方法是基于经验性的方法，如何更好地计算损伤程度值得深入探讨。

（3）桥梁维修加固对于韧性的提升相对于不同的破坏等级是有区别的，对于轻微破坏最为明显，此后逐级递减，及至结构失效时已无明显差别。在恢复函数的计算中，对于恢复函数与恢复时间的确定很大一部分是主观的，如何采集客观的数据进行韧性评估，这无疑是重要且有意义的。

参考文献：

葛俊颖.2013.桥梁工程软件 Midas Civil 使用指南[M].北京：人民交通出版社.

黄勇，张良，乐威杰，等.2017.桥梁抗震研究的近期进展[J].地震工程与工程振动，37（6）：166-174.

李世安.2009.考虑反复荷载作用的部分预应力混凝土梁桥长期挠度计算方法[D].西安：长安大学.

李秀芬，吴佩刚，赵光仪.1997.高强混凝土梁抗弯疲劳性能的试验研究[J].土木工程学报，（5）：37-42.

孙振凯，邹其嘉.1999.公路桥梁地震易损性和震后恢复过程[J].华南地震，（2）：62-70.