嘉峪关光化楼砖墙结构对抗震性能的影响

巴振宁 焦鹏 刘冰松 张翔

摘要：以嘉峪关光化楼为研究对象，基于榫卯、斗拱节点、柱墙接触之间的关系，利用ANSYS软件分别建立了纯木结构与砖木混合结构的光化楼模型。通過模态分析和输入多种地震波进行动力时程分析，结果表明：①砖墙结构大大提高了光化楼低阶自振频率，在高阶振型中自振频率的差距逐渐减小;②砖墙结构使结构在地震时程分析下的加速度峰值有了明显增大，这与结构自振周期降低有关;③在地震作用下，砖墙结构使结构的位移峰值显著减小，对防止木构架侧移倒塌有很大贡献;④纯木结构模型位移反应较大，但仍小于木结构建筑弹塑性层间位移角1/50的限值;⑤在Ⅷ度罕遇地震作用下，砖墙结构底部及开洞处的塑性应变较大，具体可能表现为砖墙底部以及砖墙与木门连接处出现裂缝。

关键词：光化楼;纯木结构;砖木混合结构;模态分析;时程分析

0 引言

中国木结构建筑文化源远流长，留有许多宝贵的文化结晶。嘉峪关建筑群始建于公元1372年，建成后经历了多次的损毁与修缮。1987年，嘉峪关建筑群被联合国教科文组织列入《世界文化遗产名录》。我国是一个地震多发的国家，嘉峪关位于世界上最大的地震带“喜马拉雅—环太平洋地震带”的作用区。因此对嘉峪关木构城楼进行抗震研究和保护，具有十分重要的意义。

国内外一些建筑大师，如梁思成（1983）、伊东忠太和陈清泉（2014）对我国的古建筑进行了系统的研究。随着力学学科体系的发展，对结构的整体和不同构件的研究也有了迅速发展。周乾等（2014）建立故宫太和殿有限元模型响应谱，分析了在Ⅷ度罕遇地震作用下，太和殿结构的内力及变形;谢启芳等（2018）以西安钟楼为研究对象，建立了缩尺比例为1：6的模型进行振动台实验，得到了在不同幅值、不同地震波作用下模型的加速度、位移和破坏形态;潘毅等（2019）以饶益寺大佛殿和保国寺的铺作层为参照，设计了4种不同的铺作层布置模型，进行动力时程分析，研究不同铺作层布置对地震激励作用下结构产生的动力响应的影响;Uchida等（2004）、Kawai等（2006）和Fujita等（2008）分别对日本传统的多层木塔与庙宇结构进行了侧向静力试验，结合日本地区地震记录数据，建立层模型并分析在地震作用下各节点与结构整体的动力响应特点。

上述研究分别对不同的木结构建筑进行了研究分析，但大多集中于受力结构，而忽略了围护结构。木结构古建筑的形制复杂，构件的应用组合多样，再加上木材的特性，不同建筑都有其独特的结构状态，值得研究。嘉峪关木构城楼第一层为砖木混合结构，第二、三层为木结构。一层金柱嵌固在砖砌体墙内，因此砖墙对木结构力学性能势必有所影响。本文采用有限元数值模拟方法，建立嘉峪关光化楼木结构有限元分析模型与砖木混合结构有限元分析模型，分别输入Ⅷ度多遇、设防与罕遇的地震波激励，分析砖墙结构对抗震性能的影响。

1 数值模型

1.1 光化楼简介

光化楼始建于公元1506年，位于嘉峪关东城台之上，城台平面为矩形，台面采用条砖十字缝墁地，城台下有拱券式门洞。嘉峪关建筑群如图1所示。

光化楼为典型的抬梁木构城楼，屋顶样式采用单檐歇山顶式。由图2可见，一层柱分内外两周，共计28根（檐柱18根、金柱10根），为贯穿三层的通柱，层高约4.4 m;二层有外廊，柱分内外两周，廊柱18根，层高约4 m;三层无外廊，共计檐柱10根，层高约3.7 m。建筑一层为砖木结构，采用砖墙，二、三层为木结构，采用槅扇，砖墙包裹金柱，厚约1.3 m，周长约41.5 m，东西两侧开门，门高2.55 m、宽2.12 m。

1.2 单元选择

光化楼模型采用ANSYS有限元分析软件进行模拟。对于传统木结构古建筑，结构主体部分主要由梁柱构架组成，采用Beam188 单元对其进行数值模拟。Beam 188单元在每个节点上有6个自由度，包括沿X，Y，Z轴的线位移和绕X，Y，Z轴的角位移，适合分析细长到中等长度的梁结构。

对于屋盖、楼板和砖墙结构，采用Shell181单元进行建模。该单元内各节点含有6个自由度，常用于模拟平板和曲壳等形式的结构，能够传递单元弯矩并在非线性计算中考虑壳厚度的变化。

对于木结构榫卯、斗拱节点，采用Combin14弹簧单元进行模拟，该弹簧单元可以传递轴力、剪力和弯矩，通过2个节点来定义，可以设置6个方向的弹簧刚度。

1.3 材料参数及边界条件设置

对木结构进行结构分析验算时，材料性能强度不仅要满足《木结构设计规范》（GB 50005—2017）的规定，还应该考虑荷载长期作用和木质老化的影响，对木材的各项力学性能指标给予调整。本文将木材本构关系简化为理想弹塑性，遵循Hill屈服准则。

由于对嘉峪关光化楼缺乏直接的实验数据，参照祝松涛（2013）对嘉峪关关楼的研究，其木材为红松，为正交异性材料，木材参数见表1。将红松的各个方向材料性能简化为理想弹塑性，此处假定木材的受拉与受压方向的屈服强度相同，采用Hill准则与BISO模型结合的方式进行定义，即通过Hill准则定义6个方向不同的屈服强度，采用BISO模型进行切线模量的定义，此处切线模量定义为0，各个方向屈服强度值参考王玉迪（2018）对红松木材的研究，见表2，理想弹塑性模型如图3所示。其中考虑到光化楼修建完成距今已经超过500年，根据《古建筑木结构维护与加固技术规范》（GB 50165—92）中对考虑长期荷载作用和木质老化调整系数的规定，对强度等性能均乘以0.7的折减系数。

朱才辉等（2019）曾对同为明代建筑的西安明代城墙以及钟楼的砖墙砌体进行过研究。结合其得出的砖墙砌体等效力学参数，并参考《砌体结构设计规范》（GB 50003—2011），本文采用的砖砌体墙材料力学参数见表3。

式中：σD，εD为考虑损伤因子的应力与应变;损伤因子D为0～1，数值越大表示结构的损伤程度越大，光化楼砖墙结构无明显破坏且本文主要考虑砖墙结构对抗震性能的影响，因此D取0;ε0为对应于砌体抗压平均值的应变，根据朱才辉等（2019）的研究，取0.003。砌体结构的应力-应变曲线如图4所示，采用MISO模型进行定义。

斗拱是古建筑中主要的结构连接形式，由多层木块交叠、咬合而成，其动力学特性十分复杂，在地震等外力荷载作用下，斗拱可以视为一组弹簧，通過自身挤压变形，减缓结构的变形，并且吸收掉一部分振动能量。本文采用Combin14弹簧来模拟斗拱半刚性的特性。梁柱榫卯节点与斗拱，均具有半刚性连接特点，同样简化为Combin14单元。斗拱、榫卯各个方向自由度的刚度值参考高大峰等（2008）、苏军（2008）的试验以及数值模拟分析结果，节点刚度取值见表4。

中国古建筑结构普遍通过柱础与地基相连接，柱根一般搁置在础石之上，在主体结构的重力作用下，础石能够为柱脚提供竖直方向的支撑力和

水平方向上一定的摩擦力，对柱根的转动具有微弱的限制。参考高大峰等（2008）、苏军（2008）中对木结构古建筑的处理方法，本文将柱脚与础石的连接节点近似简化为铰接节点;光化楼一层砖墙将金柱包裹在内，牢牢嵌固，将墙柱连接设置为刚接。

1.4 建立数值模型

光化楼的梁柱框架组成了主要的结构受力体系，主体结构可以划分为屋架层、铺作层以及柱网层。屋架层主要由梁、枋、檩条等组成的梁架体系来支撑屋顶以及传递上部荷载;铺作层主要以斗拱为主，对各层起承上启下的作用;柱网层是光化楼结构的竖向支撑部分，将整栋楼所承担的荷载传导到台基上。对主体结构逐层建立无砖墙结构数值模型（以下简称模型1），如图5a所示。

砖砌体墙是由砌块混合砂浆等粘合剂制作成的受力结构，主要受到砌块材料性能的影响，但由于砂浆等粘合剂的材料特性与砖砌体存在显著差异，所以砂浆等粘合剂对结构整体的影响也不可忽视。且结构的整体力学性能还受到诸如砖砌体尺寸、砌缝的宽度以及砖墙的砌筑方式、工艺水平等因素的影响。

目前，常用的砖砌体墙的有限元建模方法包含分离式和整体式2种。分离式建模方法就是对砖砌体墙的2种材料分别进行建模，并对2种材料接

触面做出定义以模拟其工作性能。整体式建模方法就是将砖砌体墙视为均质的各向同性材料，忽略结构模型中局部的材质差异。采取整体式建模方法时，可以适当简化砖墙结构的材料本构与力学参数，大大简化了建模难度和运算过程，适合于将砖砌体墙的看作宏观整体的有限元结构分析，本文采用该方法将砖墙结构按照图纸进行建模，其中东西向砖墙按照门尺寸进行开洞，尺寸为2.12 m×2.55 m，最终建立有砖墙结构数值模型（简称模型2），如图5b所示。

2 模态分析

模态分析是研究结构系统特性的一种方法，主要用于求解结构的自振频率、模态振型等固有振动特性。对于古建筑来讲，对其地震荷载作用下振型的分析，是结构动力学分析的基础。通常情况下高阶模态的权重远低于低阶模态，一般取前几阶模态进行分析。

本文采用子空间法提取数值模型模态，子空间法在提取中大型模型且小于40阶振型时具有较高的精度。数值模型振型频率值变化如图6所示。由图可知，嘉峪关光化楼数值模型前20阶的频率均分布至0～10 Hz，自振频率随阶数增大逐渐增大，在高阶时增长逐渐变缓。

砖墙结构的存在使结构低阶自振周期显著减低，在高阶振型中自振频率逐渐趋于一致，对结构整体刚度有较大的贡献，对光化楼整体的动力性能有显著影响。

3 抗震性能分析

3.1 地震波的选取

根据《建筑抗震设计规范》（GB 50011—2010），嘉峪关处于Ⅷ度抗震设防区，基本加速度为0.2 g，进行时程分析时根据多遇地震、设防地震、罕遇地震分别调幅为70 gal，200 gal，400 gal 3种不同加速度峰值的地震波。选取的地震波分别为El-Centro波、Taft波与兰州波。以200 gal峰值地震波为例，其地震影响系数如图7所示。

3.2 阻尼确定

阻尼作为一种能量耗散机制，使振动等运动随时间减弱并最终停止。采用瑞利阻尼进行设置，其阻尼矩阵C由质量矩阵M和刚度矩阵K表示为：

根据俞茂宏等（1991）、Fang等（2001a，b）对木结构整体动力试验测试与现场环境脉动试验，测定其阻尼比为2%～9%，一般小于5%，本文阻尼比取3.5%。根据之前模态分析结果，模型1：α=0.241 3，β=0.003 336;模型2：α=0.498 1，β=0.001 605。

3.3 加速度反应分析

对模型输入水平双向地震波，由于Y向建筑尺寸小于X向，故输入地震波时Y向与X向峰值加速度比为1∶ 0.85，采用前文所述9条地震动记录进行输入，模型加载工况见表5。

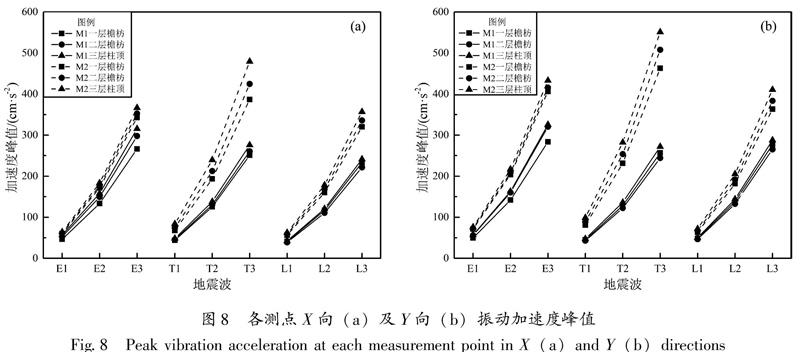
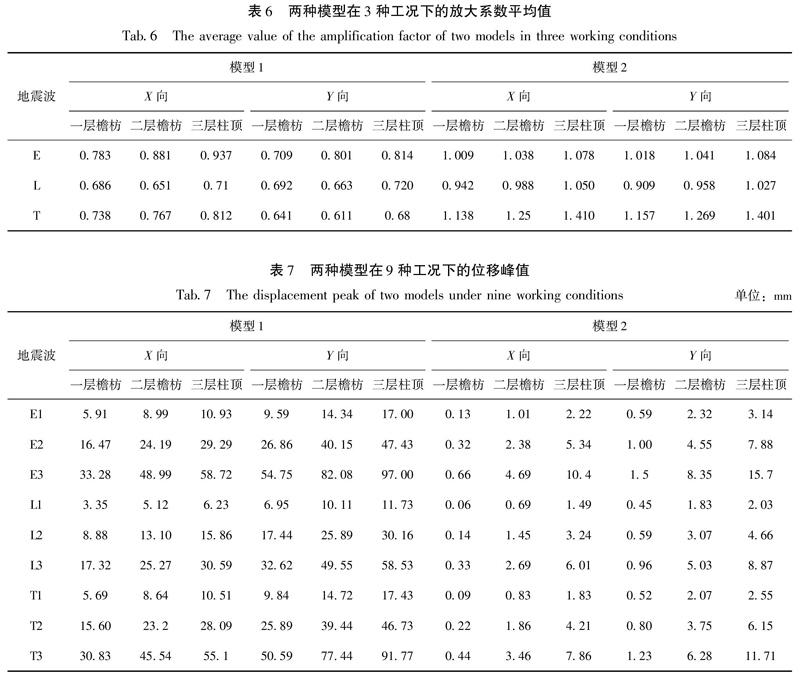
为分析不同地震加速度峰值下光化楼地震响应，分别选择一层檐枋、二层檐枋、三层柱顶位置，提取其动力响应数据。所有工况作用下的测点的振动加速度峰值如图8所示，所有工况作用下的放大系数平均值见表6，7。

由图8，表6可知：在水平地震作用下，随地震波激励的增加，各层的加速度峰值也随之增大。模型1（M1）加速度响应放大均小于1，模型2（M2）加速度响应值均有所提高，尤其是在Taft波作用下，加速度响应峰值增大1倍左右，这与砖墙结构降低了结构的自振周期，使其接近Taft波的卓越周期有关。

3.4 位移反应分析

选择一层檐枋、二层檐枋、三层柱顶位置，提取其位移响应数据。由于文章篇幅限制，仅展示模型1与模型2三层柱顶在L1，L2，L3三种工况作用下的位移时程曲线如图9所示，所有工况位移峰值见表7。

由图9，表7可知，在水平地震作用下，考虑砖墙结构的情况下，各层位移的相应峰值均减小，这反映了砖墙结构对木构架的位移有很强的约束作用，对防止木构架侧移倒塌有很大贡献。模型1在峰值为400 gal的El-Centro波作用下短轴向和长轴向出现最大层架位移角，分别为1/68和1/111，小于木结构建筑弹塑性层间位移角1/50的限值。

3.5 墙体塑性应变

光化楼开洞处横墙、未开洞处横墙以及纵墙在400 gal的El-Centro波作用下产生的等效塑性应变情况如图10所示。由图可知，未开洞墙体底部的塑性应变明显高于上部，开洞墙体的塑性应变在底部与开洞部位更为明显。这表明墙体在Ⅷ度罕遇地震波作用下，墙体底部以及墙体与木门连接处容易出现裂缝等震害。

4 结论

本文以嘉峪关光化楼为原型，根据其一楼为砖木混合结构的特点，建立了有限元数值模型，通过动力时程分析，讨论了砖墙结构对光化楼抗震性能的影响，得到以下结论：

（1）金柱与砖墙结构牢牢嵌固在一起，形成环箍效应，大大高了结构的抗侧刚度。在模态分析时，砖墙结构的存在对结构的低阶振型影响较大，光化楼结构的低阶自振频率显著提高，高阶自振频率与无砖墙结构自振频率随振型阶数的增加逐渐相等。

（2）砖墙结构的存在使建筑物加速度响应峰值有所提高，这与建筑物自振周期的变小有关。

（3）砖墙结构使建筑物位移峰值显著降低，有助于防止木结构位移过大产生侧移倾覆。

（4）对层间位移角进行了计算，嘉峪关光化楼在不同地震波作用下產生的最大层间位移角均符合相关规范的限值规定。

（5）在Ⅷ度罕遇地震作用下，墙体的底部与开洞处的塑性变形较大，墙体底部以及与木门连接处易产生裂缝。

参考文献：

高大峰，赵鸿铁，薛建阳.2008.木结构古建筑中斗栱与榫卯节点的抗震性能—试验研究[J].自然灾害学报，17（2）：58-64.

梁思成.1983.营造法式注释[M].北京：中国建筑工业出版社.

刘桂秋.2005.砌体结构基本受力性能的研究[D].长沙：湖南大学.

潘毅，袁双，郭瑞，等.2019.铺作层布置对古建筑木结构抗震性能的影响[J].土木工程学报，52（3）：29-40.

苏军.2008.中国木结构古建筑抗震性能的研究[D].西安：西安建筑科技大学.

王玉迪.2018.考虑松动残损直榫节点的多层木结构古建筑抗震性能分析[D].西安：西安建筑科技大学.

谢启芳，王龙，张利朋，等.2018.西安钟楼木结构模型振动台试验研究[J].建筑结构学报，39（12）：128-138.

伊东忠太，陈清泉.2014.中国建筑史[M].长沙：湖南大学出版社.

俞茂宏，刘晓东，方东平，等.1991.西安北门箭楼静力与动力特性的试验研究[J].西安交通大学学报，25（3）：55-62.

周乾，闫维明，关宏志，等.2014.罕遇地震作用下故宫太和殿抗震性能研究[J].建筑结构学报，35（S1）：25-32.

朱才辉，刘钦佩，周远强.2019.古建筑砖-土结构力学性能及裂缝成因分析[J].建筑结构学报，40（9）：157-186.

祝松涛.2013.嘉峪关关楼抗震性能分析及研究保护[D].西安：西安建筑科技大学.