基于峰谷分析算法用针刺仪测定树木年龄的可行性分析

潘 虹，卢 军，郭旭展，唐守正，高瑞东，徐建军

(1. 中国林业科学研究院资源信息研究所，北京 100091；2. 信阳师范学院数学与统计学院，河南 信阳 464000；3. 管涔山国有林管理局，山西 宁武 036700；4. 管涔山国有林管理局羊圈沟林场，山西 五寨 036200)

活立木年龄微损测量是解决很多林业问题的关键，对森林经营、生长模拟以及古树保护等都具有重要的意义[1-4]。传统的确定活立木年龄是通过识别树木的年轮数量[5-6]，这种方法虽然比较准确，但是需要用生长锥取树木生长芯，或者伐倒树木截取圆盘，对树木具有侵入性和破坏性；无损的确定活立木年龄的方法有查数轮生枝法和建立非线性数学模型[7-11]等，由于树木有时一年形成二层轮枝，查数轮生枝法确定树木年龄精度不高；通过建立数学模型来估算树木的年龄方法不具有普遍性，并且准确性较低[12]，实际生产中并不能得到广泛的应用。

树木针刺仪是微损的测定树木年龄的工具，将其应用于活立木，可以获得相对阻力折线图[13]，折线图中峰谷的趋势反映树木年轮内早材和晚材边界引起的变化[14]，可以估计树木的年龄和树木生长率[15-16]。树木针刺仪自带DECOM 软件可以对抗钻阻力折线图进行分析，通过人工干预半自动检测年轮边界，估计树木年龄[17]，由于针刺仪的钻针轴直径只有1.5 mm，对树干的损伤很小，使用针刺仪确定树木年龄的方法对活立木伤害小，是微损的设备，但是DECOM 软件自动识别结果很不准确，很多真实年轮边界不能正确识别，误差很大，无法在林业生产中投入使用。

本研究以德国RINNTECH 公司生产的树木针刺仪（Resistograph 4450P/S）钻入活立木获取的抗钻阻力值序列折线图为研究对象，给出峰谷分析算法，根据确定阈值Det，记录关键点值和关键点序号，来分析利用峰谷分析算法估计活立木年龄的可行性，为针刺仪自带DECOM 软件改进提供理论支撑，推进微损测定树木年龄方法的研究进程。

1 数据

从吉林汪清金沟岭林场天然林中选取52 株活立木作为研究对象，试验树木选择的都是树干通直，没有病虫害，健康活立木。试验树木包括红松(Pinus koraiensis Sieb. et Zucc.)20 株 、 冷 杉（Abies fabri（Mast.）Craib）32 株，红松的年龄分布范围是42 a 至88 a，冷杉的年龄分布范围是35 a 至92 a。首先使用生长锥取出通过髓心的树芯，共获取52 个有效树木生长芯作为参考样本。然后将针刺仪垂直于树干中心，分别在取树芯钻孔位置上下方5 cm 以内进行针刺，确保针头尽可能钻过髓心，抗钻阻力值自动保存记录，每个树芯对应一组抗钻阻力值，获取红松的抗钻阻力数据为40 组，冷杉的抗钻阻力数据64 组，共104 组有效抗钻阻力数据作为研究样本。对参考样本进行抛光、打磨和扫描，借助WinDENDRO 年轮分析系统软件确定树木的年轮数。

2 方法

2.1 针刺仪测量原理

德国RINNTECH 公司开发的树木针刺仪（Resistograph 4452P/S）是通过电脑控制电子传感器的钻刺针，测量树木的钻入阻抗，获取抗钻阻力折线图，横坐标轴刻度代表针头钻入的深度（单位： mm）， 纵坐标轴刻度为阻力值（ 单位：resi）。根据阻力和密度之间的线性关系，可以利用折线图中波峰波谷的趋势来确定活立木早材和晚材边界[18]。使用针刺仪自身携带的DECOM 软件可以自动分析折线图，识别年轮边界，估计树木的年龄。

2.2 峰谷分析算法

由于树木春材和秋材的密度不同，相应抗钻阻力值总会有差异，在抗钻阻力折线图中可以很直观的看到很多波峰和波谷出现，其中有很多跃度较小的峰谷，并不代表年轮变化。峰谷分析算法可以根据实测树芯年轮数，确定跃度的阈值Det，去掉伪年轮，留下真年轮，并将有效的年轮峰值和谷值记录下来，确定最终有效的峰谷数来估计树木的年龄。

2.2.1 确定阈值和极值点 首先对获取的抗钻阻力剖面进行去首尾处理，去掉两端无效数据，保留木质部的数据，处理后的针刺仪获取树木的相对阻力记录为整数序列 x ={x1, x2,···, xn}， n为针刺仪测量点的序列号。峰谷分析算法是从抗钻阻力序列 x起始点 k0开始，设定阈值Det，允许误差 e = 0.2，确定峰值点和峰谷点序号，以及相应的极值。各项初始值如下：

极值点进入点：

K max = k0,K min = k0,

极大值点起始进入点和退出点分别记为：

K max sta = K max,K maxend = K max,

极小值点起始进入点和退出点分别记为：

K min sta = K min,K minend = K min,

极值点 X max = X(k0),X min = X(k0)，极值点起始点 K sta = 0。

分成3 种情况进行分析：从起始点 X (k0)以后未知升降段、升段、降段。

输入为： x，Det，e， k0，升降段表示islor2，取值为0,1,2，其中islor2=1 表示升段，islor2=2 表示降段，islor2=0 表示未知升降；

输出为：极值点起点序号 Ksta，极值点最后一点序 号 Kend ， 极 值 点值 Vmid； 升降 段 表示is12 = YZ 两位数， Y 是本段代码， Z是下段代码，is12 =-1表示出错；其中，

Y = 1表 示本段升， Y = 2表 示本段降， Y = 3表示本段是头（不完整段）；

Z = 1表 示下段升， Z = 2表 示下段降， Z = 3表示下段是尾（不完整段）；

流程图见图1:

2.2.2 记录关键点序号和值，统计峰谷点个数 根据2.2.1 节得到的极值点起点和退出序号，以及升降段表示，记录峰点和谷点的数量，以及关键点值和关键点号。参数说明如下：

根据2.2.1 节输出极值点起点序号 Ksta，极值点最后一点序号 Kend ，极值点值 Vmid；升降段表示 i s12 = YZ 两位数，将参数 i s12 = YZ拆分成两个参数 id1和 id2，

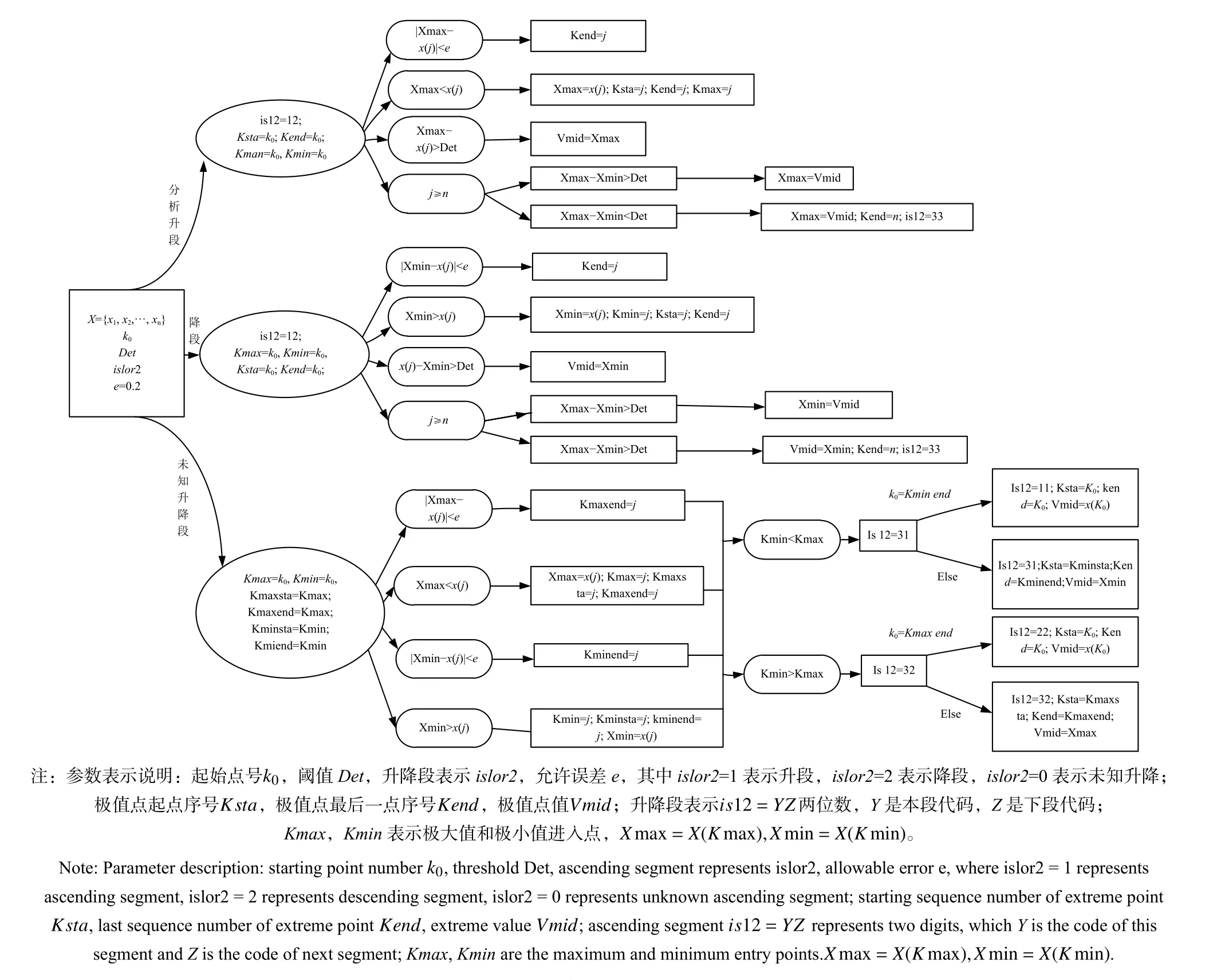
图1 峰谷分析流程图Fig. 1 Peak-valley analysis flow chart

则有：

id1 = 1表 示本段升， id1 = 2表 示本段降，id1 =3表示本段是头（不完整段）；

id2 = 1表 示下段升， id2 = 2表 示下段降，id2 =3表示下段是尾（不完整段）；

用 id1 = 1表 示波峰， id1 = 2表 示波谷，id1 =3表示端点；

矩阵P 为 m行3 列矩阵，第一列记录关键点号，第二列记录关键点值，第三列记录 id；

矩阵 N为1 行2 列的矩阵， N =(No1,No2)，其中 N o1统 计峰点的个数， N o2统计谷点个数。

2.3 步骤

输入：针刺仪测量数据去首尾得到的列向量X ={x1, x2,···, xn}和阈值Det；

step1. 将原来针刺仪数据去首尾，得到的数据

step2. 分析初始段

此 时 取 参数islor2=0， k0= 1， e = 0.2， 根 据

2.2.1 得到相应的输出Ksta,Kend,Vmid,is12。

若 id2 = 3， 记录矩阵P 为 m行3 列矩阵，第一列记录关键点号，第二列记录关键点值，第三列记录 id。X ={x1, x2,···, xn}， 加上一列序号 X1={1,2,···,n}, 分别以 X1作 为第一列， X作为第二列，构造矩阵的DX，则矩阵DX 表示带序号的观测值，可以表示为：

若i d2 = 1，分成两种情况讨论：

若i d1 = 3，此时有不完整前段，记录

若 i d2 = 2，此时后段是完整段，分成两种情况讨论：

step3. 初始段之后，各段轮流升降

当 Kend ＜n时 ，取参数islor2=id2， k0= Kend，e = 0.2，根据2.1.1 节得到相应的输出Ksta，Kend，Vmid，is12。记录 P为分块矩阵，将所有的关键点序号和关键点值依次循环写入，即

输出：矩阵 P ， 矩阵 N o =[No1,No2]。

峰谷分析算法的估计年龄 A可以由峰谷数的均值的二分之一取整数得到，即 A =(No1+ No2)/4取整数。

2.4 年轮宽度计算

根据2.3 节输出的结果矩阵 P ， P 中的第一列是关键点序号，即峰点起点序号和结束点序号以及谷点起点序号和结束点序号，第二列是关键点值，第三列表示关键点序号是峰点或者谷点。由于针刺仪的取样规律是每1 mm 取100 个点，说明抗钻阻力两个相邻的序号之间的距离就为0.01 mm，假设矩阵 P每个波峰的第一个波峰点所在的行号为

提取 P 所有的 li,i = 1,2,···,No1行，重新组成新的矩阵，记为

将矩阵 Q中的第一列相邻两个元素做差分，得到相邻两个峰点之间序号之差，因针刺仪抗钻阻力数据采取间隔是每1 mm 取100 个点，则相邻序号差值的百分之一可以是对应年度树木的估计年轮宽度，年轮宽度单位为mm。

3 结果

根据树芯的实测年龄， 选择适当的阈值Det 后，将峰谷分析算法应用于104 组活立木抗钻阻力序列，能够较好地去除树木伪年轮。图2 为研究样本红松3 的峰谷分析结果图，当选择阈值为54 时，得到的峰谷数均值为45，与实际年龄吻合，将峰谷关键点值和关键点序号连线标记可以直观看出，峰谷值跃度低于54 的峰谷点都被忽略，只留下峰谷值跃度大于等于54 的峰谷点。可以看出，确定恰当的阈值后，峰谷分析算法估计的年龄与实际年龄非常接近。峰谷分析算法估计年龄平均绝对误差是－2，范围在－5 年至5 年之间，平均相对误差为－2.69%，范围在－6.73% 至6.73% 之间；每组数据的相对误差分布见图3。

对真实年龄与算法估计年龄进行成对数据t-检验，数据检验得到t 值为1.31，由于 |t2| ＜2.2622，故不能拒绝原假设，即可以为峰谷分析算法估计树木的年龄均值与树木的真实年龄均值无显著差异，此时检验的 p值为0.192。

4 讨论

4.1 峰谷分析方法的优点

本算法数据是基于树木针刺仪获取抗钻阻力值，由于针刺仪的钻针直径小，对树木损害小，与传统的树木年代学方法估计树木年龄[19-20]相比较，本算法估计树木年龄是属于微损的，或者准无损的方法，适用于受保护的天然林管理和古树年龄鉴定。由于针刺仪体积小，质量轻，属于便携式设备，克服了以往仪器测定树木年龄法的笨重、操作繁琐等缺点，便于野外试验进行操作。

4.2 提高针刺仪测定树木年龄精度的可行性

针刺仪自身携带有年轮分析软件DECOM，能对获取的抗钻阻力数据自动划分年轮边界，但是通过与参考样本获取的实际年轮数对比发现，自动检测的年轮边界准确率较低，平均相对误差为－92.27%。使用DECOM 软件检测年轮边界时，需要靠人工经验进行视觉判读，手动添加年轮边界，耗时，效率低。而本算法通过MATLAB 编程实现，将抗钻阻力值作为峰谷分析算法的输入，根据实测树芯年龄来选择适当的参数Det 值，可以得出树木的估计年龄，并且与实际年龄误差较小，平均相对误差降低至－2.69%。树木针刺仪通过峰谷分析算法测定树木的年龄是可行的。

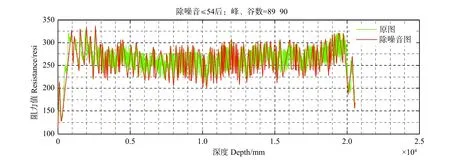
图2 红松3 峰谷分析结果Fig. 2 Peak-valley analysis results of Korean pine 3

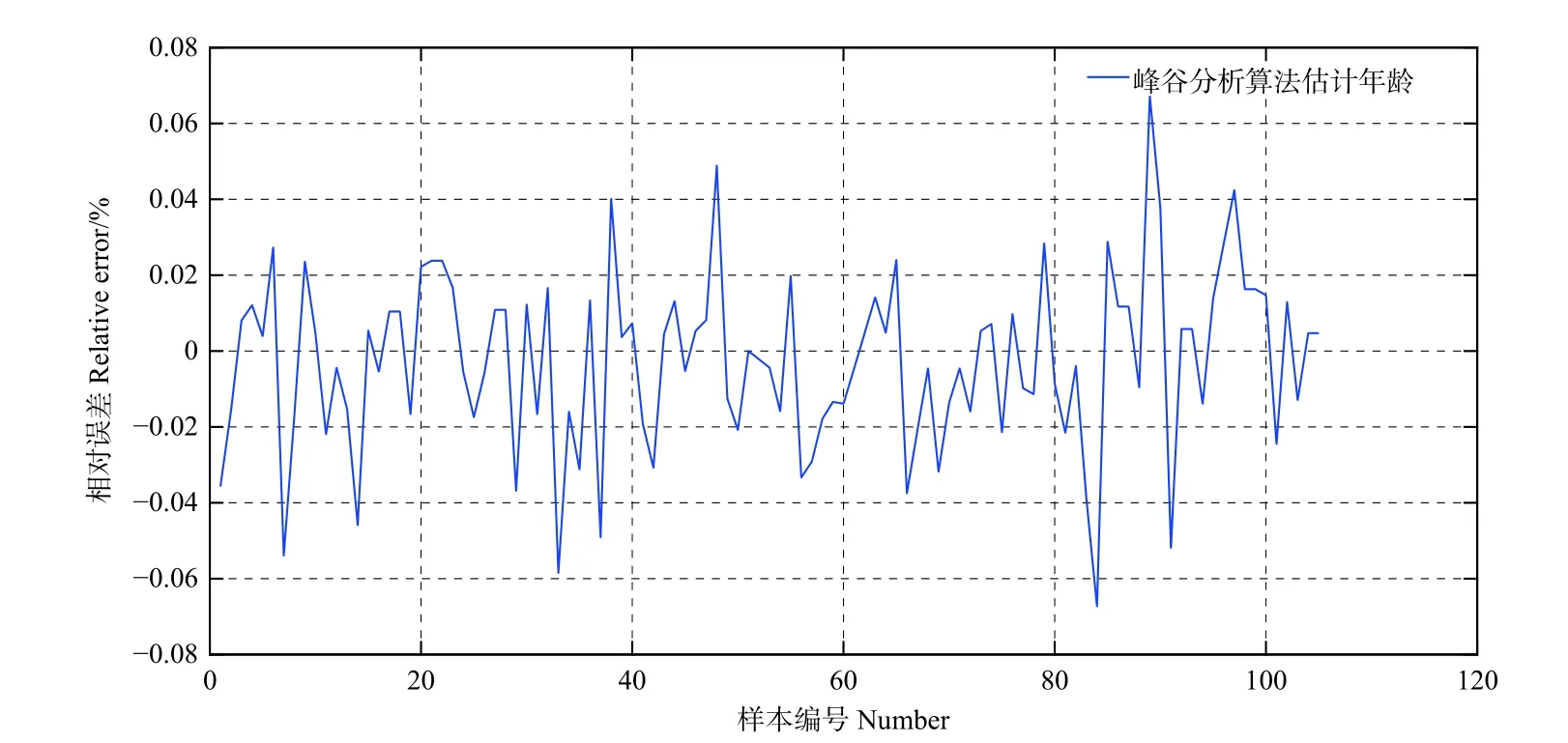
图3 峰谷分析算法估计年龄与实测年龄相对误差分布Fig. 3 Relative error distribution between Peak-valley analysis algorithmand true age

4.3 阈值Det 选取

峰谷分析过程中，设置了很多过程参数来辅助描述分析细节，分析过程细致周密，并且使用起来非常方便。峰谷分析算法输入端只有两个变量：抗钻阻力值序列X和阈值Det，随着阈值Det的取值不同会得到不同的峰谷数。确定阈值Det后，当峰或者谷的跃度，或者高度，超过Det之后作为一个完整段。在本研究中，红松的阈值取值范围为13～67，冷杉的阈值取值范围为6～55。由于Det的分布范围较大，可以考虑用机器学习的方法，找出每棵树的特征，来研究去掉树木的假年轮对应的恰当阈值Det值。

4.4 年轮宽度的计算

本算法输出结果中，将每棵树所有的峰点和谷点的序号，以及对应的抗钻阻力值记录到矩阵中。记录的过程采用分块矩阵的形式，为计算树木的年轮宽度提供了依据。虽然年轮宽度估计值和实测之间有差别，但是估算的树木年轮宽度能基本上反映树木的年生长趋势，可以作为估算树木连年生长量的一个参考。

5 结论

确定恰当的阈值后，通过给出的峰谷分析算法，可以将针刺仪获取的抗钻阻力数据作为输入，得出树木年龄的估计值，峰谷分析算法应用于针刺仪抗钻阻力序列来估计树木年龄是可行的，确定存在恰当的阈值使针刺仪估计树木年龄精度很高，阈值的选择依据是下一步研究的重点内容。