基于模糊理论的PMT水下防爆试验故障树分析*

谭润泽， 李晓彬， 杜志鹏， 何 苗， 乐京霞

(1.武汉理工大学交通学院 武汉，430063) (2.海军装备研究院 北京，102401)

(3.中国科学院高能物理研究所 北京，100049)

引 言

近年来，随着微观粒子物理学的不断发展，中微子作为自然界中的基本粒子之一，中微子的探测过程及应用研究已经引起了国内外的广泛关注[1-6]。目前，国内对于中微子探测已经取得了一定的进展，在建中的江门中微子探测实验室用于测定核反应堆中微子质量顺序和混合参数。

江门中微子实验利用附着在中心探测器上的2万只PMT监测光信号进而探测到中微子。随着使用时间的增长，PMT可能会在水下发生内爆，产生冲击波导致数千个PMT链式反应爆炸[7]。为防止PMT连锁内爆的发生，提出了一种PMT保护罩并设计了PMT水下防爆试验系统，以此验证保护罩的防爆性能。但是经过测试发现，试验系统未能达到预期目标。针对试验准备周期较长、系统故障具有突发性且缺乏有效评估数据等问题，引入模糊故障树分析法(fuzzy fault tree analysis，简称FFTA)对PMT水下防爆试验系统进行故障诊断分析。

FFTA是一种将模糊数学和故障树分析相结合的风险评估方法。该方法利用系统发生故障各因素间的逻辑关系，建立引起系统失效的故障树模型。Sivaprakasam等[8]基于模糊故障树理论和专家评价法对液化石油气燃料补给站泄漏进行了故障诊断分析。文献[9]针对煤矿钻探工程中的冲击地压问题，采用模糊故障树的分析方法获取了引起该故障的主要关键因素。文献[10]应用模糊逻辑理论分析船舶系泊作业故障风险，建立故障树模型，并提出了相应的风险控制方案。任玉刚等[11]利用模糊故障树分析法对“蛟龙号”液压系统进行故障诊断，并通过载荷试验验证了分析结果。综上所述，模糊故障树分析法已广泛用于工程系统的故障诊断和失效模式获取，但在中微子探测工程中未见其在PMT水下防爆试验失效概率评估方面的应用。

笔者针对PMT水下防爆试验系统故障特点，将模糊故障树应用到PMT水下防爆试验中，借助故障树模型对试验系统进行故障树构建，应用专家判断法和三角形模糊数，得到系统故障的模糊失效概率及引起故障的主要关键因素，根据故障树的关键重要度分析结果，提出试验系统改进方案，并对改进方案进行测试以验证故障诊断结果的准确性。

1 故障树模型

1.1 工程背景

江门中微子探测器置于位于地下700 m的圆柱型水池(高为45 m、直径为43 m)中心，20 000只PMT安装在金属框架结构上，探测器内外均充满液体介质，如图1所示。PMT的材料为有机玻璃，结构厚度约为4～6 mm，内部近似真空。实际工作状态下始终承受0.10～0.54 MPa的静水压力[4]。由于液体侵蚀和初始缺陷等，同时受到静水压力作用，某个PMT在工作一段时间后可能发生爆炸，引起的内爆冲击波传播至相邻PMT可能使其殉爆，从而导致链式反应爆炸。

图1 江门中微子探测器Fig.1 Jiangmen neutrino detector

1.2 PMT水下防爆试验系统工作原理

为测试PMT保护罩的防爆性能设计了防爆试验系统：通过引爆中间位置的PMT检测相邻PMT损坏状态。PMT水下防爆试验系统由液压引爆系统、压力容器系统、防爆装置和支撑固定结构组成。液压引爆系统由引爆圆盘、液压缸等组成，压力容器系统由密闭压力罐、压力传感器和加压阀等组成，防爆装置由通过横向螺钉连接的上玻璃保护罩和下金属保护罩组成，支撑固定结构主要有两部分，分为顶部引爆杆的固定结构和PMT的支撑模块。内爆试验过程中，为了模拟PMT在中微子探测器中的深水环境压力，向密闭压力容器内注水，并在水面以上保留一定的空气域，借助加压阀向空气加压，随后通过压力传感器确定静水压力值。为了引爆中间PMT，基于力平衡原理采用三点引爆的方式(单一顶部引爆装置和一对底部对称分布引爆装置)，通过液压缸带动引爆圆盘挤压PMT玻璃外壳。PMT水下防爆试验装置如图2所示。

1-顶部引爆装置；2-固定装置；3-玻璃防护罩；4-PMT；5-横向连接；6-金属防护罩；7-底部引爆装置；8-支撑模块

1.3 故障树

在分析PMT水下防爆试验系统原理及收集大量相关文献[2-6]资料的基础上，利用模糊故障树建模理论，按照能否引爆PMT的思路构建了故障树模型，如图3所示。图中试验系统失效T为顶事件(top event)，Mk为中间事件(middle event，k=1,2,…,6)，Bk为底事件(basic event，k=1,2,…,15)。基于布尔代数运算法则，采用下行法计算故障树的结构函数如下

T-试验系统失效；M1-PMT被引爆且相邻PMT破碎；M2-PMT未被引爆；M3-防护装置故障；M4-顶部引爆装置故障；M5-上保护罩存在缺陷；M6-下保护罩存在缺陷；B1-存在加工裂痕；B2-壳体厚度不够；B3-上下保护罩连接方式不合理；B4-下保护罩进水孔设计不合理；B5-下保护罩结构强度不够；B6-引爆杆强度不够；B7-顶部液压缸压力不足；B8-固定装置失效；B9-支撑模块强度不够；B10-压力传感器故障；B11-液压系统压力不足；B12-液压系统泵性能故障；B13-液压油性能下降；B14-液压缸性能故障；B15-底部引爆装置故障

(1)

简化式(1)得

T=B1+B2+…+B13+B14+B15

(2)

根据故障树的结构函数式(2)，PMT水下防爆试验故障树共有15个一阶最小割集，分别为{B1},{B2},…,{B15}。

2 模糊故障树分析方法

2.1 模糊数及故障描述

在应用传统FTA方法故障诊断的过程中，往往无法获取足够的统计数据来描述底事件的统计特性，并且对于底事件的故障程度描述存在模糊不确定性，因此较难获取各底事件精确的故障概率值。FFTA方法通过模糊数描述事件发生的概率，将故障发生中的随机性和不确定性表示为模糊可能性，引入模糊子集的隶属度概念描述故障程度。例如，某事件的故障状态为无、中等和严重，则可以分别用区间[0,1]上的模糊数0,0.5和1来代替。

(3)

其中：a1和a3为模糊集边界值;a2为模糊集中心值；当a1=a2=a3时，模糊数则为确定值。

图4 三角形模糊数隶属函数Fig.4 The membership function of trigonometric fuzzy numbers

2.2 底事件失效可能性的获取

(4)

根据式(4)计算不同专家意见的一致度，可得各个专家意见一致度矩阵

(5)

因此，专家Ei评价意见的平均一致度(average agreement，简称AA)和相对一致度(relative agreement，简称RA)为

其中：AA(Ei)为专家Ei评价结果的平均一致度；RA(Ei)为专家Ei评价结果的相对一致度。

通常情况下，不同专家拥有不同的专业知识熟悉程度和工作经验等，因此各个专家评价意见对底事件评估结果的重要度不同，需对不同专家意见进行加权平均[14-15]，引入相对重要度系数

(7)

其中：ω(Ei)为专家Ei的重要度系数；ri为根据评判标准专家Ei的得分值。

综合式(6)和式(7)可得专家Ei对于同一底事件评价的共识系数为

CC(Ei)=βω(Ei)+(1-β)RA(Ei)

(8)

其中：CC(Ei)为专家Ei评价结果的共识系数(consensus coefficient，简称CC)；β为松弛系数，0<β<1。

综上，基于模糊数学理论对各个专家的评价结果进行计算，得底事件Bk故障概率的专家组评价意见聚合模糊数

(9)

2.3 故障概率计算和重要度分析

在底事件的重要度分析中，不同底事件的模糊数结果难以比较，因此需将式(9)得到的模糊数规划为一模糊可能性的准确值(fuzzy possibility score，简称FPS)，该值表示专家评估底事件故障的最大可能性。针对文中的故障树模型及模糊数结果，应用面积中心法[16]对事件的模糊数进行逆模糊化计算，如下所示

(10)

其中：μA(x)为事件评价聚合模糊数的隶属函数。

底事件故障概率的计算方法主要有两种：统计大数据根据可靠度理论确定；应用专家判断法根据模糊理论确定。为保证两者一致性，将模糊可能性转化为模糊概率(fuzzy probability，简称FP)[17-18]

(11)

通过上述公式，可以得到各个底事件的故障概率结果。基于底事件的故障概率和故障树的结构函数，计算顶事件的失效概率为

P(T)=P(MCS1∪MCS2∪…∪MCSN)=

P(MCS1)+P(MCS2)+…P(MCSN)+…+

(-1)N-1P(MCS1∩MCS2∩…∩MCSN)

(12)

其中：P(T)为顶事件失效概率；MCSi为故障树的最小割集(minimal cut sets，简称MCS)。

为便于系统故障的诊断及改进，文中应用底事件关键重要度的计算方法，根据底事件对于顶事件发生的贡献度进行排序，关键重要度(critical importance factor，简称CIF)计算公式为

(13)

其中：CIF(Bk)为底事件的关键重要度；P(Bk)为底事件故障概率。

3 PMT水下防爆试验故障树分析

3.1 基于模糊理论的故障树分析流程

使用模糊故障树模型对PMT水下防爆试验故障可能性评估的技术路线如图5所示。首先在建立系统故障树模型的基础上，获取故障树的最小割集；按照评价标准模糊数，由专家对PMT试验故障树中各底事件的故障可能性进行评判，确定底事件故障程度，同时对专家的判断结果进行聚合平均处理；最后基于面积中心法和故障树概率计算法则，逐层计算得到顶事件的失效概率，并利用故障树重要度计算方法，确定引起试验失效的关键因素，以便提高故障分析的准确性。

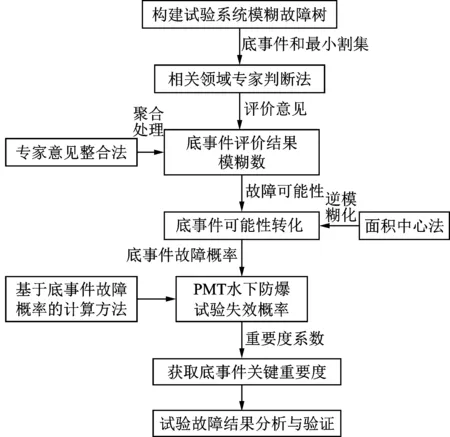
图5 基于模糊故障树的PMT水下防爆试验故障可能性评估Fig.5 Evaluation flowchart of failure possibility of experiment system for underwater PMT explosion protection based on fuzzy fault tree

3.2 PMT水下防爆试验失效概率计算和重要度分析

文中主要是对中微子探测器工程中针对PMT防爆性能的试验失效原因进行分析。根据模糊故障树理论建立试验故障树，共有15个基本事件，在故障树定量计算中缺乏底事件的故障概率，因此笔者应用7级语言评价标准[8]，由参与PMT试验系统及保护罩设计的6名专家组成的专家组预测15个底事件故障发生可能性，并按照底事件聚合模糊化理论及故障概率计算方法，获取各底事件综合考虑各专家评估结果的三角形模糊数和逆模糊化处理的故障概率，如表1所示。语言评价标准隶属函数如图6所示。

图6 语言评价标准范围Fig.6 Linguistic terms conversion scale

表1 底事件故障概率Tab.1 Fuzzy probability of basic events

由PMT水下防爆试验故障树的结构函数式(2)分析可得，各个底事件均为最小割集，因此最小割集间相互独立，根据顶事件失效概率计算方法，使用式(12)试验失效概率P(T)为4.800 36×10-2。根据上述计算结果，对比事件发生概率评定标准[17]，PMT水下防爆试验失效可能性为“较高”，与试验已经测试过的结果一致，验证了笔者基于模糊故障树分析法在PMT水下防爆试验故障诊断方面的可行性和准确性。

为确定导致试验失效的关键因素，以便改进设计方案，应用模糊故障树关键重要度计算方法，对各个底事件进行关键重要度分析，按照重要度大小对各个底事件排序，选取对顶事件影响较大的5个底事件重要度，如表2所示。

表2 底事件关键重要度Tab.2 Critical importance of basic events

由表2可知，导致PMT水下防爆试验失效的主要原因依次是下保护罩进水孔设计不合理、上下保护罩连接方式不合理和下保护罩强度不够。同时，下保护罩进水孔的设计不合理关键重要度最大，因此对于改进试验系统及提高保护罩的防爆性能效果最为明显，在实际设计过程中应着重考虑。基于模糊故障树分析方法，通过定性分析及定量分析，可快速、准确获得导致顶事件失效的关键风险因子，可有效为系统的诊断及改进设计提供参考依据。

3.3 基于故障树故障分析结果的改进方案验证

为验证故障树分析结果的准确性、提高试验系统的可靠性及保护罩的防爆性能，通过故障树的重要度分析结果，对顶事件影响较大的底事件B4,B3及B5进行改进，并对改进后的系统重新进行测试。

1) 针对事件B4保护罩进水孔设计不合理，对保护装置的进水孔面积进行了测量，发现未考虑PMT底部与下保护罩之间缝隙的面积，因此对此区域加圆盘覆盖，并重新计算引起相邻PMT破碎的冲击波阈值对应的总进水面积，将下保护罩进水孔直径改为Φ75 mm。下保护罩进水孔设计改进前后变化，如图7所示。

2) 针对事件B3上下保护罩连接方式不合理，对上下保护罩连接处进行反复检测，发现通过螺钉加垫圈的横向连接方式，会导致上下保护罩连接过紧，从而在冲击波压力作用下在连接处产生较高的应力集中，进而导致试验失效，因此将上下保护罩连接方式改为螺栓加销钉的纵向连接。连接方式改进前后变化，如图8所示。

图8 PMT防护装置测试连接方式改进Fig.8 The improvement connection type of PMT protection device

3) 针对事件B5下保护罩强度不够，对下保护罩结构强度重新进行有限元计算，发现只设置一对称分布的加强筋，则导致下保护罩在冲击波作用下在未设置加强筋的一侧变形较大，因此改为四周均设置加强筋固定。改进后下保护罩加固方式如图9所示。

图9 PMT防护装置固定方式改进Fig.9 The improvementstructural fixation of PMT protection device

基于上述故障树分析结果及改进方案，对PMT水下防爆试验系统重新进行保护罩防爆性能验证，改进后的测试结果如图10所示。由图10可知，在引爆中间PMT后，相邻PMT(红色框内)未发生破损，有效阻止了链式反应爆炸。是否安装改进保护罩的PMT侧部冲击波压力对比如图11所示。由图11可知，未安装PMT保护罩的冲击波压力为11.2 MPa，安装改进后的保护罩后，冲击波压力减小仅为2.3 MPa。上述结果验证了改进方案的合理性以及改进方案能够有效提高保护罩的防爆性能，同时也进一步验证了基于模糊故障树分析方法在PMT水下防爆试验故障诊断方面的可行性和准确性。

图10 改进装置测试结果Fig.10 Test result of improved device

图11 冲击波压力时历曲线Fig.11 Pressure-time curres of shock wave

4 结束语

笔者提出一种基于模糊故障树理论的PMT水下防爆试验失效可能性评价方法，应用模糊集理论和专家意见评价法，获取各底事件发生概率，可降低概率确定过程中的模糊不确定性，使故障树分析的结果更加准确。通过基于模糊故障树的PMT水下防爆试验失效评估方法获取导致系统失效的关键故障，提高了系统故障诊断效率。应用模糊故障树分析结果及改进方案，进行保护罩防爆性能测试，结果分析表明，保护罩能够有效阻止PMT连锁内爆，验证了该评估方法的可行性，可为PMT水下防爆试验及后续江门中微子探测器的故障诊断提供参考。