解题的“金钥匙”——勾股定理

文 江苏省无锡市河埒中学八（15）班 周焱辉

在解决问题的过程中，我发现勾股定理就是一把解题的“金钥匙”。例如：

如图1，已知正方形ABCD的边长为6cm，E为边AB上一点且AE的长为1cm，动点P从点B出发以每秒1cm的速度沿射线BC方向运动。把△EBP沿EP折叠，点B落在点B′处。设运动时间为t秒，请问：是否存在某一时刻t，使得点B′到直线AD的距离为3cm？

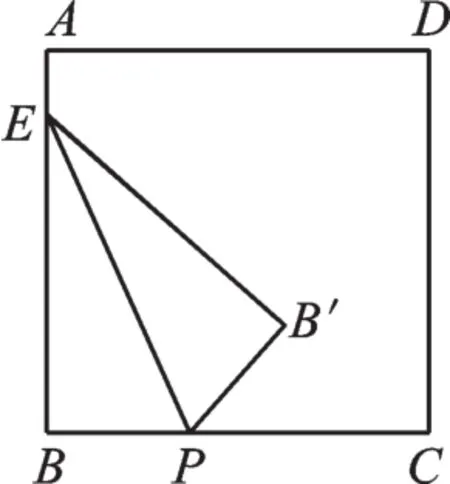
图1

图2

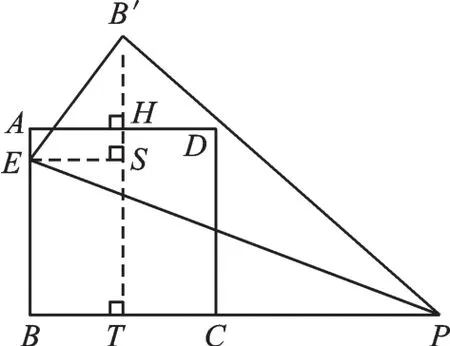
图3

要破解这道题，首先要作B′H⊥AD。B′H=3，值得注意的是点B′可能在AD的下方或上方，而点P又在射线BC上运动，所以完全可能有这样的两种情况。

情况一（如图2）点B′在AD下方（此时点P在线段BC上）。由翻折可知：BP=B′P，想用勾股定理，可BP、B′P均不在“现成”的直角三角形中，怎么办？没有，就“造”呗！延长HB′交BC于T，在Rt△B′PT中，可得B′T=3，但PT未知。一时似乎没有头绪，再仔细检索各个已知条件，不难发现，过点E作ES⊥HB′，在Rt△ESB′中，ES2+B′S2=EB′2，所以，BT=ES=，由此，在 Rt△B′PT中求得B′P，从而求出t。

情况二（如图3）点B′在AD上方（此时点P在线段BC的延长线上），延长B′H交BC于T，过点E作ES⊥B′T，在Rt△ESB′中，ES2+B′S2=EB′2，可求出ES=3。这时，PT可以表示为t-3，PT所在的三角形为Rt△PTB′，由已知可得B′T=B′H+6=9，根据B′T2+PT2=PB′2列方程，可得t。

感悟：只要找到了解题的“金钥匙”——勾股定理，我们就可以很快地找到解题思路。与“金钥匙”配套的“锁”是直角三角形，有时当题目图形中没有现成的直角三角形时，我们需要根据已知条件或图形，结合问题，添加辅助线，构造直角三角形来解题。

教师点评

在不具备解决问题的条件时，我们要善于“创造”条件。运用勾股定理解决问题的前提是直角三角形，我们不但要有发现有价值的直角三角形的眼力，还要有构造直角三角形的能力。我们要学会将陌生的问题向熟悉的问题转化。