一种16-QAM+周期互补序列集的构造方法

万梦华，李 琦，高军萍，岳红翠，李 琛

(河北工业大学 电子信息工程学院，天津 300401)

0 引言

互补序列[1]具有理想的自相关性能和互相关性能，可以完全消除多径干扰和多址干扰，在导航系统、码分多址系统、多入多出信道估计、室内无线红外通信系统等领域具有广泛应用[2]。随着各类序列设计理论研究的不断深入[3-4]，QAM周期互补序列集成为互补序列设计中的研究热点[5-6]。QAM周期互补序列具有较高的数据传输速率和频谱效率，比传统的扩频序列更有优势，但其数目不能满足通信系统应用的需求，成为限制其应用的一个障碍。

为了提高系统容量的要求，2010年Boztas等人提出了QAM+的概念[7]，增加了满足通信工程应用的扩频序列数目。因此QAM+序列的构造和研究受到越来越多的关注。2014年研究学者对8-QAM+序列的构造方法做了一个总结[8]。2015年研究学者提出了一个最优16-QAM+零相关区序列集的构造方法[9]。2017年笔者提出了分别基于二元周期序列集和三元完美序列构造16-QAM+周期互补序列集的方法[10]。

本文提出了一种16-QAM+周期互补序列集的构造方法。将16-QAM周期互补集与三元周期互补序列集结合，生成了16-QAM+周期互补序列集，进一步增加了互补序列数目。

1 基本定义

定义1设两个长度均为N的周期序列分别表示为γ={γ(t)}=(γ(0),γ(1),…,γ(N-1))和d={d(t)}=(d(0),d(1),…,d(N-1))。则γ和d的周期相关函数为

(1)

(2)

取周期互补序列集V中的任两个序列Vl1和Vl2(l1≠l2)。若Vl1和Vl2的相关函数满足

(3)

则称周期互补序列集V中的所有序列两两互为伴集。

定义316-QAM+星座的字母表定义如下：

3+j,3-j,-3+j,-3-j,1+3j,

1-3j,-1-3j,-1+3j,3+3j,3-3j,

-3+3j,-3-3j}

其中，j2=-1。

定义4设3个长度均为N的周期序列，分别表示为ν={ν(t)|0≤t≤N-1}、σ={σ(t)|0≤t≤N-1}和c={c(k)|0≤k≤N-1}。序列c中的每个元素可通过以下运算得出：

，

(4)

式(4)在QAM+序列的构造过程中具有重要作用[11]。

2 16-QAM+周期互补序列集的构造

本文以PCSS16-QAM和PCSS3为初始序列集，通过式(4)相互结合生成PCSS16-QAM+，以下为具体构造过程：

(5)

(6)

(7)

(8)

(9)

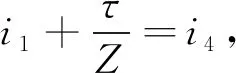
(10)

(11)

定理3步骤3所得的序列集C是一个PCSS16-QAM+(LH,MP,NZ)。

(12)

Cl,h中所有子序列自相关函数之和为

(13)

综上所述，C是一个PCSS16-QAM+(LH,MP,NZ)。

定理4周期互补序列集C中的LH个序列两两互为伴集。

(14)

结合定理2得出的结论，则序列Cl1,h1和Cl2,h2的互相关函数为

(15)

综上所述，序列集C的LH个序列两两互为伴集。

3 具体实例

取PCSS16-QAM(2,2,4)序列集V的任不同的两个序列V1和V2，且二者互为伴集。如下所示：

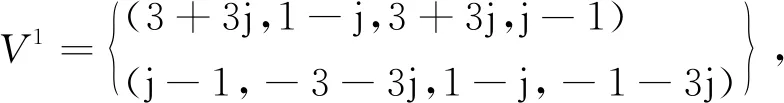
取PCSS3(2,2,7)序列集S的任两个不同的序列S1和S2。且二者互为伴集。如下所示：

则生成的PCSS16-QAM(4,4,28)序列集C的4个序列分别是

4个序列Cl,h(l=1,2h=1,2)中所有子序列自相关函数之和均为

0,0,0,0,0，0,0,0,0,0,0,0,0,0,0,0,0,0,0),

4个序列之间的6个相关函数均为

0,0,0,0，0,0,0,0,0,0,0,0,0,0,0,0,0,0),

其中，l1≠l2或者h1≠h2，并且l1,l2∈{1,2}h1,h2∈{1,2}。

4 结论

本文基于16-QAM周期互补序列集和三元周期互补序列集生成16-QAM+周期互补序列集。所得的16-QAM+周期互补序列集与初始的16-QAM周期互补序列集相比，其互补序列个数和子序列长度均得到了不同程度的扩展，并且新构造的互补序列两两互为伴集，为多址通信工程应用提供更多可选多元序列集。