核转折点裁剪表示的时间序列异常检测算法

展 鹏，陈 琳 ，曹鲁慧，许浩然，李学庆

1.山东大学 软件学院，济南 250100

2.山东大学 信息化工作办公室，济南 250100

1 引言

时间序列是日常生产过程中无处不在的一种数据类型，其广泛存在于医疗诊断[1-2]、网络监测[3]、金融经济[4]、水文分析[5]、能源电力[6]等各种行业中。随着信息化、物联网等先进技术的飞速发展，时间序列数据正以惊人的速度不断积累，如何从海量的时间序列中挖掘潜在有价值的信息已经成为学术界和工业界的研究热点。正如杨强教授在文献[7]中指出，时间序列数据挖掘已经成为21世纪十大最富有挑战性数据挖掘领域的研究方向之一。

在时间序列数据挖掘相关研究内容中，时间序列异常检测一直备受国内外研究人员关注。不失一般性的，时间序列异常检测是指发现时间序列中与其他对象最不相似的数据序列或数据点的集合[8]。通常，时间序列异常检测通常可以分为数据点异常检测和数据序列异常检测[9]，本文主要研究序列异常检测。由于时间序列具有数据维度高、数据量大且持续积累等天然特性，直接利用传统的数据挖掘方法进行异常检测往往难以获得令人满意的检测效率，且原始时间序列数据在采集过程中难免夹杂大量噪声数据，对异常检测结果的准确性与可靠性亦会产生影响。如Keogh等[8]提出的基于距离的时间序列暴力异常检测算法（Brute Force Discord Discovery，BFDD）因时间复杂度为O(m2)，实际应用开销过大，难以应用于高维度、大数据量的时间序列。因此，对时间序列进行异常检测之前，通常需要对时间序列进行降维表示，即将高维的原始序列转化成低维的特征表示形式。

多年来，国内外研究人员对时间序列降维表示展开了深入研究，提出了多种降维表示方法，整体上可以划分为四类[10]：数据自适应方法、数据非自适应方法、基于模型的方法以及数据驱动的方法。常用的时间序列降维表示方法主要有分段线性表示（PLR）[11-12]、分段聚合近似表示（PAA）[13]、符号化表示（SAX）[10，14]、域变换表示（DFT、DWT）[15-16]、裁剪表示（Clipped）[17-19]等。针对基于时间序列降维表示的异常检测，国内外研究人员做了大量研究并提出了一系列有效的方法。Keogh 等将时间序列转换为符号化表示形式，利用基于启发式的异常发现算法，优化内外循环检测过程，提出了HOTSAX[8]异常检测算法。Khanh等将可索引的符号化表示iSAX与WAT 算法相结合，提出了WATiSAX[20]异常检测算法。周大镯等提出了一种基于重要点分割的K近邻时间序列局部异常检测算法[21]，该算法通过计算待检测时间序列的局部异常因子LOF[22]进而发现异常序列。相关研究成果表明，基于降维表示的时间序列异常检测不仅有效提升了异常检测效率，同时能够确保检测结果的有效性和稳定性。

在众多降维表示方法中，基于数据驱动的时间序列裁剪表示[17]是一种简单、直观的降维表示方法，它依据时间序列中数据点与序列均值的关系将原始时间序列转换成一组由0 和1 组成的序列。通过这种策略，有效地实现了对原始时间序列的压缩，减少了存储成本。此外，基于裁剪表示的下界距离计算方法使得其支持与原始时间序列比较相似性，因而能够获得更紧密的下界距离，进而确保基于裁剪表示的时间序列检索、聚类、异常检测等过程的高效性和无漏报（no false dismissals）。然而，传统的裁剪表示方法忽略了时间序列中数据点对序列趋势变化的影响，并且存在着无法自定义降维表示压缩率的缺陷。

综上所述，本文提出了一种可自定义压缩率的、基于核转折点的时间序列裁剪表示方法（Kernel Turning Points Clipped Representation，KTPC）。在此基础上，提出了基于KTPC 表示的时间序列异常检测算法（KTPC-based Anomaly Detection，KTPC-AD）。本文详细分析了算法的执行过程与特点，对算法时间复杂度做了细致解析，通过实验对比分析，验证了该方法在时间序列异常检测方面的有效性与高效性。

2 相关定义

2.1 时间序列

时间序列中的每一个数据观测值通常可表示为一个元组(ci,ti)，代表在时刻ti所记录的数据值为ci[1，12，23]，由此，本节给出了时间序列的定义。

定义1（时间序列）时间序列是一种按照时间顺序递增而不断累积的数据观测值的有序集合，可将其形式化表示为：

其中，n为时间序列的长度。由于时刻t是严格递增的，因此，本文将时间序列简记为：

就时间序列异常检测领域而言，人们更关注某段时间区间内的异常情况，即局部的异常，称之为时间序列子序列[1]。

定义2（时间序列子序列）对于一个给定的时间序列C，子序列X是C中的一个连续片段，即X是长度为m(m≤n)且从时刻j(1 ≤j≤n-m+1)开始连续采样m次所得，可形式化表示为：

为了检测时间序列中的异常子序列，通常采用滑动窗口（Sliding Window）[1，11]技术将时间序列划分成一系列的子序列，以形成子序列集合，见定义3。

定义3（子序列集合）对于一个给定的时间序列C，利用滑动窗口技术将时间序列C划分成一系列的子序列，可形式化表示为：

XS即为子序列集合，其中N为子序列的数量。若滑动窗口大小为w，滑动步长为e，则子序列集合XS中每个元素可形式化表示为：

其中，Xi为子序列集合XS中第i个子序列。该子序列首位数据值的时刻j可根据滑动步长e计算所得，即j=(i-1)×e+1；末位数据值的时刻根据首位时刻与滑动窗口大小w计算得出，即j+w-1。

2.2 时间序列裁剪表示

基于数据驱动的裁剪表示方法是一种直观、高效的降维表示方法，该方法由Ratanamahatana 等人最先提出[17]。裁剪表示方法根据时间序列中每个数据点与当前序列均值的大小关系，将原始时间序列转换成一组由0 和1 组成的序列。定义4 给出了时间序列裁剪表示[17]的表示过程。

定义4（裁剪表示）对于一个给定的长度为n的时间序列C，令其裁剪表示形式记为ˆ，则ˆ中每个元素由公式（6）计算所得：

其中，μ为时间序列C的均值。如公式（6）所示，当时间序列C中元素ci大于均值μ时，其对应的裁剪表示形式cˆi设定为1，否则设置为0。为形式化展示裁剪表示的处理过程，图1 所示为一段时间序列数据经过裁剪表示后的结果，原始时间序列即表示为000000001100111111111100。

图1 时间序列裁剪表示

从图1可以看出，位于均值线μ以上的数据点映射为1，μ以下的点映射为0。裁剪表示方法的降维表示效率非常高，适用于表示高维度、大数据量的时间序列数据。然而，传统的裁剪表示方法忽视了时间序列中数据点对序列趋势变化的影响程度是不同的这一事实，即均等对待每个数据点。同时，降维表示的压缩率完全由数据自身决定，而无法自定义压缩率。

为了解决如上问题，Son等人提出了一种基于感知重要点（Perceptually Important Points，PIP）[24]的裁剪表示方法IPIP[18]。IPIP方法首先将时间序列划分成若干分段的形式，然后提取每个分段中的PIP，最后利用公式（6）将分段中的PIP转换成0和1的形式。IPIP方法利用对时间序列具有重要表示特征的PIP进行裁剪表示，同时通过自定义PIP 提取数量来控制数据的压缩率。然而，PIP的提取过程时间复杂度相对较高，一定程度上影响了IPIP 方法在相似性检索、异常检测等领域的应用。随后，Son等人采用分段中间点作为特征点进行裁剪表示，从而简化了特征点提取方法，称为MP_C 方法[19]。MP_C方法不仅保留着裁剪表示方法的高效优势，同时可通过自定义中间点提取数量来控制数据压缩率，而且，中间点提取过程较PIP提取更加高效。但是，MP_C方法采用分段中间点作为裁剪表示特征点同样忽视了时间序列中数据点对序列趋势变化的影响程度不一的事实。

在前期工作中发现[11-12，25-26]，时间序列中对序列趋势变化有重要贡献的数据点往往更能够表现原始时间序列的形态特征，将基于特征数据点的降维表示方法应用于时间序列检索、分类、异常检测等研究领域中，能够有效提升数据分析的精度。结合当前裁剪表示方法存在的问题，本文提出了一种基于核转折点的时间序列裁剪表示方法KTPC，该方法不仅支持可自定义的数据压缩率，而且简化了核转折点的提取过程，有效提升了KTPC的降维表示效率。

2.3 时间序列异常检测

时间序列C经滑动窗口划分成子序列集合XS后，本文所提异常检测算法即是从XS中找到那些不正常的子序列集合。不失一般性的，异常得分是时间序列异常检测方法中一种重要的反馈异常的方式，基于异常得分的异常检测方法需要根据设定的阈值来判断待检测对象是否为异常[27]。由此，本文给出了异常得分及异常子序列的相关定义。

定义5（异常得分）对于一个给定的时间序列子序列集合XS，其中子序列Xi∈XS，令ϑi表示子序列Xi的异常得分，即表示子序列Xi相较于XS中其他子序列的差异程度。

定义6（异常得分集合）对于一个给定的时间序列子序列集合XS，其中每条子序列的异常得分组成了XS的异常得分集合AOS，可形式化表示为：

令表示异常得分集合AOS的均值，则子序列Xi的异常平均指数ζi由公式（8）计算得出：

定义7（异常子序列）对于一个给定的时间序列子序列集合XS，γ记为子序列异常阈值。若子序列Xi的异常平均指数ζi满足不等式ζi ＞γ，则Xi可定义为异常子序列。

3 核转折点裁剪表示方法KTPC

时间序列随着数据值的变化，其波动趋势会呈现不同的形态，如股票价格走势、网络流量变化等等。转折点（Turning Point，TP）[11，14]是引起时间序列趋势变化的特征点，可依此作为裁剪表示的重要特征点。

图2 KTPC裁剪表示过程

定义8（转折点）对于一个给定的时间序列子序列X，若数据点ci∈X使以下任意一项不等式成立，则数据点ci为转折点（TP）。

起伏波动是时间序列的常见现象，虽然TP 能够反映时间序列的数值变化，然而每个TP 对序列局部走势的影响程度各有差异。文献[11]中将TP 到时间序列均值的垂直距离（Vertical Distance，VD）作为其对时间序列局部影响程度的指标，其中，VD是时间序列降维表示过程中常用的一种权重度量方法[11，14，28]。该方法存在一定的局限性，即是位于均值附近的TP易被忽略。因此，为了定量描述TP 对时间序列局部走势的影响程度，同时有效发现处于均值附近的TP，本文给出了转折点重要指数的定义，如定义9。

定义9（转折点重要指数）对于一个给定的时间序列子序列X，其中包含的转折点为{TP1,TP2,…,TPi,…} ，记μ、maxX、minX分别为子序列X的均值、最大值与最小值，则转折点重要指数TII可由公式（10）计算所得：

分析公式（10）可知，TII 是指数据点距离子序列均值和上（下）边界VD 的最大值。当数据点大于均值μ时，将数据点到均值μ和最大值maxX的VD中最大值作为其转折点重要指数，反之，则将数据点到均值μ和最小值minX的VD 中最大值作为其转折点重要指数。转折点的TII值越大，表明该转折点的权重越高，可优先选取其作为降维表示的特征数据点。为此，结合TII 的定义，本文给出了核转折点的定义。

定义10（核转折点）对于一个给定的时间序列子序列X，其中包含的转折点为{TP1,TP2,…,TPi,…} ，转折点对应的TII表示为{TII1,TII2,…,TIIi,…} 。按照TII从大到小排列，则TII处于前l位的转折点，即定义为核转折点（KernelTP，KTP）。

完成以上相关定义后，基于核转折点的时间序列裁剪表示方法KTPC 的降维表示过程可大致分为以下三个步骤，如图2所示。

步骤1对于一个给定的时间序列C，利用滑动窗口技术将C划分为时间序列子序列集合XS，其中每条子序列Xi的长度均为滑动窗口大小w。接下来，即是对子序列集合XS中的每条子序列进行KTPC 表示处理。

步骤2取出子序列集合XS中的任意子序列Xi进行KTPC 表示。为详细描述KTPC 表示过程，以图3为例进行说明。如图3 所示，X1为XS中的第一条子序列，其长度为200。将X1等分成K(K=4) 个分段（Segments），分别为{Segment1，Segment2，Segment3，Segment4}，分段的长度均为50。利用定义8 对转折点的定义即可发现子序列中全部的TP，如图3中圆形点与方形点所示，可以看出，每个TP对子序列的局部波动影响程度是不同的。由此，根据定义9 计算每个TP 的转折点重要指数TII。如图3 中Segment1 所示，点虚线即为TP 距离子序列均值μ和上（下）边界VD 的最大值。随后，将每个分段中的TP按照TII降序排列，取TII值处于前(l=4)位的TP作为KTP，如图3中方形点所示。

图3 子序列的KTPC表示过程示意图

本文对TII的计算进行了优化，即取TP偏离均值或上（下）边界的最大值作为其重要性指数，确保位于序列均值附近的转折点可被选取作为特征表示数据点。得到子序列各分段中的KTP后，利用公式（6）将KTP转换为0和1的表示形式。最后，将子序列Xi的每个分段的裁剪表示结果进行合并，形成Xi的KTPC表示结果Xˆi。

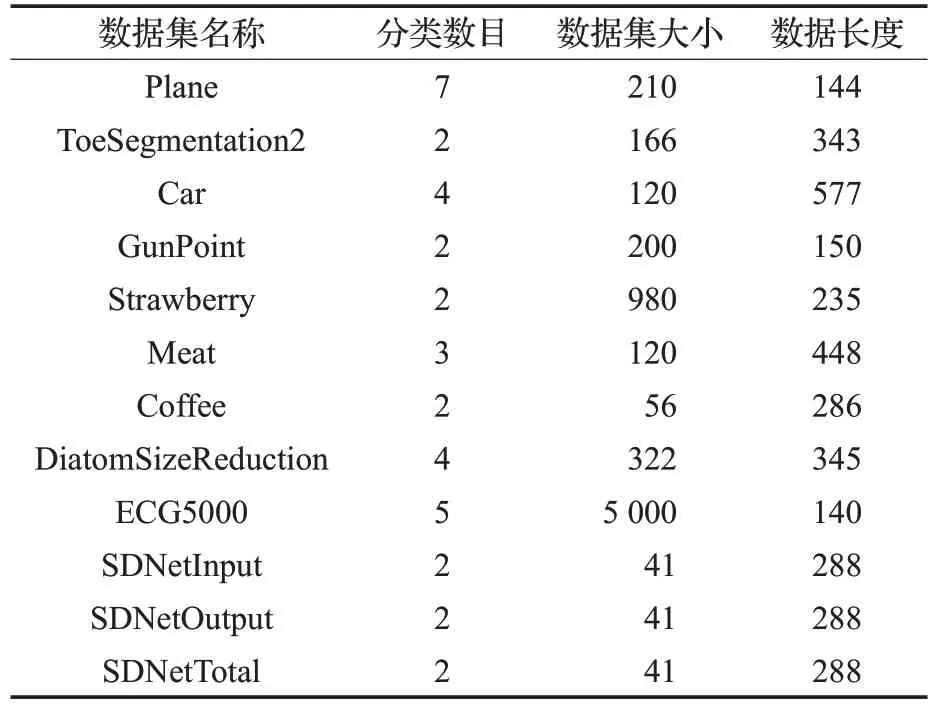
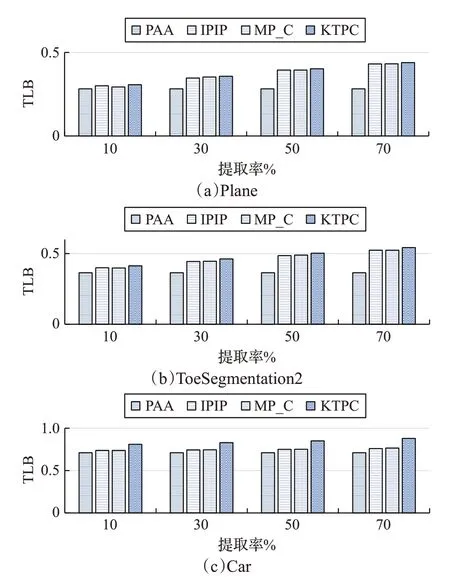
特别地，若时间序列的波动特征不明显，即子序列中TP较少，在子序列划分成若干分段后，分段中的TP点个数tpc

步骤 3将步骤 2 中子序列的 KTPC 表示结果Xˆi存入表示结果集合，随后，将子序列集合XS中下一条子序列Xi+1移入KTPC表示方法，按照步骤2中过程进行表示处理，并将相应表示结果存入表示结果集合。直至XS中全部子序列均已完成KTPC表示。

为了确保利用KTPC 表示结果进行时间序列异常检测不会出现漏报，需要定义基于KTPC表示的下界距离计算方法。假设给定两条长度为n时间序列X和Y，形式化表示为：X={x1,x2,…,xn} 和Y={y1,y2,…,yn} 。时间序列Y经过KTPC表示后的结果为Yˆ。在计算X与Yˆ的下界距离前，需将X转换到与Yˆ相同的特征空间中，需要说明的是，在将X转换的过程中，只需标记特征点的索引位置，无需将数据值转换成0 和1 的模式。综上，基于KTPC表示的下界距离可由公式（11）计算所得：

公式（11）由两部分组成，分别是两条序列各分段均值的距离和ˆ中核转折点与序列X对应索引位置数据点的距离。其中，K为子序列的分段数量，h为每个分段的长度，和分别表示子序列X和Y中第i分段的均值，l为KTP数量，表示ˆ中核转折点与序列X对应索引位置数据点的距离。DKTPC(ˆ)的具体计算过程与IPIP和MP_C方法类似，计算方法和下界证明可参考文献[18-19]，本文不再赘述。

4 KTPC-AD时间序列异常检测算法

KTPC 方法实现了对原始时间序列的降维与特征表示，配合符合下界要求的距离计算方法DKTPC，可确保异常检测过程中不会出现漏报。因此，本文基于KTPC表示，提出了一种高效的时间序列异常检测算法KTPC-AD。

为了衡量时间序列中子序列之间的差异程度，本文定义了基于KTPC 的差异性评估矩阵（KTPC-based Difference Evaluation Matrix，KDEM），见定义11。

定义11（基于KTPC的差异性评估矩阵）对于一个给定的时间序列C，其子序列集合为XS={X1,X2,…,Xi,…,XN} ，共N条子序列。任意两条子序列间的DKTPC距离构成了KDEM，如公式（12）：

计算得出KDEM之后，根据定义5对子序列异常得分ϑ的定义，公式（13）给出了ϑ的计算方法：

定义5至定义7给出了基于KTPC的异常子序列的定义，结合以上公式可以看出，异常得分ϑ即是子序列X较子序列集合XS的异常得分平均水平的偏离程度，ϑ值越大，说明子序列的异常程度越高，配合定义6与定义7，即可得出异常子序列。

综上所述，KTPC-AD方法的伪代码如算法1所示。

算法1KTPC-AD

输入：时间序列C，滑动窗口w，移动步长e，分段个数K，核转折点提取个数l，异常阈值γ。

输出：异常子序列集合ASList。

1.XSList=ConvertTS(C,w,e)；//将时间序列转换成子序列集合

2.L=sizeof（XSList）；//获取子序列个数

3.KTPCList=KTPCRepresentation（XSList，K，l）；//将子序列转换为KTPC表示

4.Initializes KDEM filled with 0;

5.foriin 1：Ldo

6.forjin 1：Ldo

7.KDEM（i，j）=DKTPC(Xi,Xˆj)；//计算子序列间的下界距离

8.end for

9.end for

10.AOS=calculateAnomalyScores（KDEM）；//计算子序列的异常得分

11.AIS=calculateAnomalyIndex（AOS）；//计算子序列的异常平均指数

12.foriin 1：Ldo

13.ζi=AIS[i]；

14.ifζi ＞γthen

15.InsertXiintoASList；

16.end if

17.end for

18.returnASList；

5 算法分析

5.1 KTPC时间复杂度分析

对于一个给定的时间序列C，令滑动窗口大小为w，子序列集合XS的容量为L，KTPC表示中分段数为K，每个分段提取的核转折点数为l。对于时间序列子序列集合中的一条子序列X，KTPC表示的时间复杂度可以从以下三个方面进行分析：

（1）在长度为w的子序列X查找转折点并计算转折点重要指数的时间复杂度为O(w)。

（2）根据核转折点的定义，当计算获得转折点重要指数后，在每个分段中提取l个核转折点的时间复杂度为O(K×l)。

（3）最后，将核转折点表示成0和1的序列形式的时间复杂度为O(K×l)。

已知，不等式K×l≤w是成立的。因此，对于一条子序列，KTPC表示的时间复杂度不超过O(w)。综上，对于一个给定的时间序列C，KTPC表示的时间复杂度不超过O(L×w)。

5.2 KTPC-AD时间复杂度分析

利用KTPC 方法对时间序列C进行裁剪表示后，即可基于裁剪表示结果进行异常检测。算法1 给出了KTPC-AD 的算法执行过程伪代码，该算法的时间复杂度可从以下两个方面进行分析：

（1）根据KTPC 表示结果，首先需要构建差异性评估矩阵。由此分析，基于KTPC的相似性距离DKTPC的时间复杂度为O(K×l)，构建KDEM的时间复杂度则为O(L2×K×l)。

（2）KDEM 构建完成后，计算子序列异常得分、异常平均指数以及判断是否异常子序列的时间复杂度均为O(L)。

综上所述，KTPC-AD 算法时间复杂度不超过O(L2×K×l)。

6 实验结果与分析

本章通过在开源数据集[29]及网络流量时序数据集上的对比实验，从下界距离紧密性（Tightness of Lower Bound，TLB）、降维表示效率以及异常检测精度三个方面来检验本文提出的KTPC 和KTPC-AD 方法的有效性。实验软硬件环境如表1所示。

表1 实验环境

本章实验数据采用了Keogh 博士团队整理的UCR时间序列分类数据集[29]，以及采集自山东大学核心网络设备的网络流量时序数据。根据数据的不同分类，实验所使用的数据集如表2所示。

表2 实验用时间序列数据集

结合上文介绍，KTPC主要参数为分段数K和核转折点的提取个数l。由于不同类型时间序列的数据长度是不同的，本章实验采用特征点提取率cr来计算每个分段的特征点数量l，如公式（14）：

其中，sn表示每个分段的数据点个数。

6.1 下界距离紧密性对比实验

下界距离是在时间序列特征表示空间下的距离计算，下界距离的好坏通常用紧密性（TLB）来衡量，TLB可由公式（15）计算得出：

其中，DLB(X′,Y′)为时间序列在降维表示空间下的下界距离，D(X,Y)为时间序列间的实际距离。由公式（15）可以看出，TLB 取值范围为0～1，TLB 越接近1，说明在当前表示空间的下界距离越接近真实的距离，下界距离的表现越好。

图4所示为4种降维表示方法（PAA、IPIP、MP_C和KTPC）在三种时间序列数据集上的TLB结果对比。其中，该实验中设置分段数K=4，横坐标为提取率cr。分析图4 实验结果，PAA 方法采用分段均值降维表示原始时间序列，因此数据特征损失较严重，下界距离与实际距离差距较大，因此TLB较低；IPIP、MP_C与KTPC方法均采用特征点进行裁剪表示，由于KTPC 方法中利用高效核转折点提取方法，有效获取了对原始时间序列局部特征有重要影响程度的点，因此，基于KTPC表示的下界距离与实际距离的差距较小，即拥有最大的TLB。

不失一般性的，本节在同等实验条件下，使用4 种降维表示方法对实验数据集进行TLB对比实验，求对实验结果进行平均处理，如表3所示。

图4 三种数据集上不同方法的TLB实验结果

表3 不同方法的平均TLB实验结果%

由于PAA 方法不受提取率cr影响，因此其TLB 结果在不同压缩率情况下是相同的。随着特征点提取率的提高，TLB随之提升，这是因为获取的特征点越多，越能够表征原始时间序列的数据特征，结合公式（11）可知，相应的下界距离也会随之增大，进而引起TLB的提升。综合分析表3可知，KTPC方法具有最高的TLB，即KTPC 方法较另外3 种基准方法具有更紧密的下界距离，在时间序列检索、异常检测等应用中，配合相应的索引结果，能够更准确地发现目标序列。

6.2 降维表示效率对比实验

降维表示的执行效率是衡量一种降维表示方法是否高效的重要指标。本节将KTPC与其他5种表示方法进行对比实验，进而分析KTPC方法的高效性。

为了比较各方法在不同分段数K下，运行时间的变化趋势，本节首先设计实验，将特征点提取率设置为cr=10%，将6 种方法在不同分段数K的条件下，应用于实验数据集上，最后将各数据集的表示时间进行平均化处理。为了便于分析各个方法的平均运行时间的变化趋势，本节以PAA方法在K=4 情况下的平均运行时间设置标准值1，其他方法基于该值进行标准化处理，最终实验结果如图5所示。

图5 不同方法降维表示的标准化平均运行时间

分析图5可知，PAA方法首先将原始时间序列划分成K个分段，利用分段均值进行降维表示，随着分段数的增多，每个分段中的数据点相应减少，计算分段均值的平均时间有所降低，因而会出现如图5中所示PAA方法先上升后下降的趋势形态；SAX 方法先利用PAA 的思想得到每个分段的均值，然后利用查找表将分段均值表示成字母形式，因而平均运行时间稍高于PAA，形态特征与PAA 方法一致；Clipped 方法是原始的裁剪表示方法，不受分段数控制，因而其平均运行时间未见明显波动，而且其通过一次遍历即可得到降维表示形式，效率很高；MP_C 方法先将时间序列分成K个分段，然后寻找分段的中间值作为特征值进行裁剪表示，当K较小时，所需的特征点较少，因而表示效率很高，随着K的增加，表示所需的平均运行时间缓慢增加，但依然具有较高的表示效率；IPIP 方法与MP_C 方法类似，不同之处在于其选取特征点的方式时间复杂度较高，因而其平均运行时间也相对增加；本文提出的KTPC方法具有IPIP和MP_C方法的优点，其表示的平均运行时间低于PAA方法，KTPC利用高效的核转折点提取方法有效规避了IPIP方法的不足之处，因而其表示的平均运行时间优于IPIP方法，而略高于MP_C和Clipped方法。

为进一步分析分段数与提取率对KTPC 表示效率的影响，图6 所示为KTPC 方法在不同分段数和提取率情况下，表示运行时间的变化趋势。整体上分析，随着分段数K和提取率cr的增高，平均运行时间也随之增加。结合图5 的实验结果，在接下来的异常检测实验中，为确保检测效率，将分段数设置为K=4，然后分析不同提取率情况下，异常检测精度的变化情况。

图6 不同提取率情况下KTPC的表示效率对比实验

6.3 异常检测精度对比实验

KTPC-AD 方法是本文提出的一种基于KTPC表示的时间序列异常检测方法。为了对比分析KTPC-AD的异常检测精度，本节设计实验将KTPC-AD 与3 种异常检测基准方法（基于SAX 表示的异常检测SAX-AD[1]、HOTSAX[8]和基于ADPAA表示的异常检测APAA-AD[30]）进行异常检测精度对比。

表4 异常检测精度对比实验

为了公正评价各方法的异常检测精度，本节引入异常检出率DR[30]作为评价标准，可形式化为公式（16）：

其中，AN为异常序列的总数，DAN为异常检测方法检测出的异常序列数量。表4 所示为各方法在不同时间序列数据集的异常检测检出率实验结果。其中，分段数设定为K=4，为分析不同提取率对KTPC-AD 方法的异常检测精度的影响，表4 列出了4 种不同提取率（10%、30%、50%和70%）情况下的KTPC-AD 方法异常检测精度。为了发现异常序列，根据定义7，本节将异常阈值γ设置为：γ=ζˉ+2×σζ。其中，ζˉ为序列异常平均指数均值，σζ为其标准差。

综合对比分析可知，SAX-AD方法因为符号化表示损失了原始时间序列的数据特征，再利用下界距离进行异常检测时，会导致无法发现一些潜在的异常，导致检出率较低；HOTSAX 利用了符号化表示和基于启发式的优化策略，配合下界距离进行剪枝操作，有效提升了异常检测效率，同时提高了异常检测精度；APAA-AD方法不同于以往基于时间域的分段表示，它分割了时间序列的数值域，利用分段在数值域上的均值表示，有效提高了异常检测精度；KTPC-AD 方法基于核转折点的裁剪表示，其具有较为紧密的下界距离计算方法，配合具有局部数据特征的核转折点裁剪表示形式，能够有效计算时间序列间的相似性，从表4 可以看出，当提取率为10%时，其异常检出率较低，这是因为核转折点数量较少，保留的原始时间序列特征难以有效区分序列间的相似度，当提取率设定为30%或更大时，异常检出率保持在较高水平，且相对稳定。通过以上分析，可使用分段数K=4，提取率cr=30%的参数配置进行时间序列异常检测，可有效提升异常检出率约15%。

7 结束语

本文提出了一种基于核转折点裁剪表示方法KTPC的时间序列异常检测方法KTPC-AD。方法首先将原始时间序列等分成若干分段，然后提取每个分段的核转折点进行时间序列裁剪表示，即将原始的时间序列数据转换表示为一组由0 和1 组成的特征序列，即KTPC 表示形式。随后，利用序列的KTPC 表示形式，结合下界距离，利用本文提出的异常得分与差异性评估矩阵，配合异常检测过程算法，有效地执行时间序列的异常检测。通过在开源数据集与网络流量时序数据集上的对比实验发现，本文提出的KTPC表示方法具有较高的表示效率，通过能够提供较为紧密的下界距离，为KTPC-AD异常检测方法提供了精度保障，实验证明，KTPC-AD方法有效提高异常检出率约15%。在下一步工作中，将针对核转折点进行再分析，进一步优化转折点重要指数的计算，使其能够以尽量少的核转折点表征更多的原始数据特征，进而提高异常检测的效率和精度。