可靠性绿色物流配送选址-路径问题研究

李 锐，李晓会，陈 鑫

辽宁工业大学 电子与信息工程学院,辽宁 锦州 121001

1 引言

配送网络是物流配送系统运作的基础。合理的配送中心选址及车辆路径规划对于配送系统的有效运作具有重要作用。选址-路径问题（Location-Routing Problem，LRP）同时集成选址问题和车辆路径优化问题。国内外学者对各种LRP 问题及其扩展问题进行了研究。Caroline 等[1]和 Michael 等[2-3]分别从不同角度对近年来LRP的相关研究进行了详细的综述，包括标准LRP，以及多阶段LRP、多周期LRP、多目标LRP等各种扩展问题。

随着环境保护意识的增强，人们也开始注意到物流配送过程中CO2排放对环境的污染。绿色的物流配送系统设计对于发展可持续物流具有重要意义。目前，对于绿色LRP 问题的研究较少。Govindan 等[4]研究易腐食物供应链中带时间窗的两级LRP问题，同时最小化成本和环境影响。Toro等[5]研究绿色有容LRP问题，最小化运作成本和环境影响。Tricoire 等[6]对城市枢纽LRP问题进行了研究，同时优化成本和CO2排放。戢守峰等[7]研究考虑库存的LRP联合优化问题，同时优化总成本和碳排放。Koç 等[8]研究考虑排放的城市货物运输LRP 问题。Dukkanci 等[9]研究绿色 LRP 问题，建立单目标优化模型，最小化运作成本及排放成本，并考虑时间窗约束。然而，以上研究并没有考虑安全性问题。

当前，各种系统的安全性越来越受到人们的关注。实际中，物流配送系统内部或外部的干扰都会给系统带来中断风险，从而影响系统的正常运作。因此，设计安全的物流配送系统具有现实意义。最近，一些学者对于考虑中断的可靠性LRP问题进行了一定的研究。Zhang等[10]研究有容LRP 问题，考虑仓库的随机中断，建立基于情景的混合整数规划模型，并设计元启发式算法求解。Xie 等[11]考虑设施以概率中断，并建立整数规划模型，设计一种拉格朗日松弛方法求解。Ahmadijavid等[12]研究中断风险下的LRP 问题，考虑随机的生产-配送中心和车辆的中断，基于风险测度建立优化模型，并设计启发式方法求解。Rayat等[13]研究集成库存的可靠性LRP 问题，同时考虑配送中心的供应中断和部分缺货。但目前为止，考虑CO2排放的可靠性LRP问题还没有得到研究。

因此，本文研究可靠性绿色物流配送选址-路径优化问题。与现有LRP 问题研究不同，本文基于NTM 方法计算油耗和CO2排放成本，定义车辆路径可靠性，以总成本最小化为目标，建立带有车辆路径可靠性约束的物流配送选址-路径优化模型，并设计一种混合帝国竞争算法求解。最后，通过实验来验证模型的合理性及算法的有效性。

2 问题描述及模型建立

如图1所示，物流配送网络包括配送中心、客户、配送车辆和配送线路。车辆从配送中心出发依次通过不同的客户进行配送后再返回到配送中心。现实中，由于不确定因素的影响，配送中心和运输线路可能发生中断。中断的发生会影响配送系统的正常运作。此外，运输过程的油耗和CO2排放会对环境造成污染。可靠性绿色物流配送选址-路径优化问题通过选择开设配送中心、优化不同车辆的行驶路径，最小化总物流成本及油耗和CO2排放成本，同时满足车辆路径可靠性约束。

图1 配送网络系统

模型假设条件如下：

（1）客户点的位置、数量和需求量已知；

（2）配送中心的位置、数量、开设成本、能力和中断概率已知；

（3）任意两点之间的距离和中断概率已知；

（4）车辆的类型不同且数量已知，每个车辆的固定运作成本、运输能力、单位距离运输成本、空载和满载油耗已知；

（5）任意一个客户点必须有且只有一辆车通过；

（6）每辆车只能从一个配送中心出发，并返回该配送中心；

（7）每个配送中心允许多个车辆驶出和驶入。

2.1 符号及变量

模型符号定义如下：

I：客户点集合；

J：配送中心集合；

M=I⋃J；

K：车辆集合；

di：客户点i∈I的需求量；

Gj：配送中心j∈J的固定开设成本；

Uj：配送中心j∈J的能力；

Pj：配送中心j∈J的中断概率；

Hk：车辆k∈K的固定运营成本；

Qk：车辆k∈K的运输能力；

Ck：车辆k∈K的单位距离运输成本；

：车辆k∈K的空载油耗；

：车辆k∈K的满载油耗；

e：油耗和CO2排放成本系数；

Dil：点i∈M到点l∈M的距离；

pil：点i∈M和点l∈M之间线路的中断概率；

τ：运营周期（τ=365）。

决策变量定义如下：

filk≥ 0 表示车辆k∈K在点i∈M和点l∈M之间的运输量。

2.2 优化模型

基于以上符号和变量定义，建立可靠性绿色物流配送网络选址-路径模型如下：

目标函数（1）最小化总成本，包括配送中心的开设成本、车辆的固定运营成本、运输成本及运输油耗和CO2排放成本，其中Filk表示车辆k在点i∈M和点l∈M之间线路的运输油耗，计算详见2.3节。式（2）为车辆k的路径可靠性约束，其中车辆路径的可靠性定义为该路径保持正常运作的概率，β为要求的可靠性水平。约束（3）表示车辆k分配给配送中心j。约束（4）表示开设的配送中心必须有车辆驶出。约束（5）表示如果配送中心没有开设，则没有车辆驶出。约束（6）表示车辆从一个点驶入，也要从该点使出，即保证路径为一个环路。约束（7）避免各个客户点之间形成子环路。约束（8）保证每个车辆至多只能从一个配送中心驶出。约束（9）保证每个客户点必须有且只有一个车辆服务。约束（10）要求任意两个配送中心之间没有车辆线路。约束（11）表示车辆的能力约束。约束（12）表示配送中心的能力约束。式（13）表示客户点两端流量的平衡约束。式（14）表示两点之间线路流量的上限和下限约束。式（15）～（17）为二值变量约束。式（18）为两点之间流量的非负约束。

2.3 运输油耗计算

本文采用NTM（Network for transport and environment）的方法来计算运输车辆油耗[14]。基于NTM 的方法，运输车辆的油耗可由式（19）计算：

其中，Fempty为空载车辆的油耗，Ffull为满载车辆的油耗，lf为负载系数。

车辆k在点i∈M和点l∈M之间线路之间的运输油耗Filk为：

3 算法设计

可靠性绿色物流配送选址-路径问题是经典LRP问题的扩展，所以也是NP-hard 问题。当规模较大时问题的求解困难，所以设计智能优化算法对该问题进行求解。

帝国竞争算法[15]是由 Atashpaz-Gargari 和 Lucas 提出的一种基于社会政治进化的智能优化算法。算法通过模拟人类社会中帝国主义殖民地竞争过程来实现对优化问题的求解。目前，ICA 算法已经应用于不同领域问题的求解，如旅行商问题[16]、静态同步补偿器的设计问题[17]、柔性作业车间调度问题[18]和混流双边装配线平衡问题[19]等，并且算法的性能已经在应用中得到了验证。

鉴于问题模型的特点，本文设计一种HICA算法对问题进行求解。HICA算法采用实数向量对问题的解进行编码，并在产生新殖民地位置的过程中引入变异和交叉操作，进而改善算法的搜索能力。

3.1 HICA算法的主要步骤

步骤1根据3.2节中解的编码方式，生成初始国家，并初始化帝国集团（详见3.3节）；

步骤2每个帝国集团中，产生新的殖民地位置（详见3.4节）；

步骤3对于每个帝国集团，交换帝国和殖民地的位置（详见3.5节）；

步骤4计算所有帝国集团的势力（详见3.6节）；

步骤5帝国之间的竞争（详见3.7节）；

步骤6消灭失去所有殖民地的帝国（详见3.8节）；

步骤7当群体中只剩下一个帝国集团，或者达到最大迭代次数时，算法终止，否则，转到步骤2；

步骤8输出势力最大的帝国。

3.2 解的编码与解码

如图2所示，问题的解可由实数向量来表示。向量由三部分组成。假设NC表示客户点数量，ND表示配送中心数量，NV表示车辆数。第一部分表示车辆经过客户点的次序，每一位对应一个客户点，取值为[0,1]之间的实数。将各个位的取值从小到大排列，即得到客户点的排序。第二部分表示客户点的车辆分配，每一位取值为[1,NV]之间实数，对其四舍五入取整得到选择的车辆号。第三部分表示车辆所属的配送中心，每一位对应一个车辆，取值为[1,ND]之间实数，四舍五入取整对应的整数表示车辆选择的配送中心。

图2 解的表示

假设客户点的数量为4，配送中心数量为3，车辆数量为2。那么，客户点编号为1～4，配送中心编号为1～3。根据第一部分值得到客户点的排序为3-4-2-1。根据第二部分值可得客户点1、3分配给车辆1；客户点2、4分配给车辆2。再由第三部分值可得车辆1分配给配送中心3，车辆2 分配给配送中心1。最后，可得车辆1 的行驶路径为配送中心3➝客户3➝客户1➝配送中心3，车辆2的行驶路径为配送中心1➝客户4➝客户2➝配送中心1。根据上述解码规则，给定向量的取值可以唯一确定每辆车的行驶路径，进而可以确定变量xilk、yjk的值，再由约束（4）和（5）即可确定解zj。

3.3 初始化帝国集团

随机生成数量为Npop的初始国家。选择势力最大的Nimp个国家作为帝国主义国家，剩下的Ncol个国家作为殖民地国家，其中Ncol=Npop-Nimp。

根据帝国主义国家的势力大小分配殖民地，按照式（21）～（23）计算帝国分配的殖民地数量：

其中，cn为帝国n的代价函数（详见3.9节）；Cn为标准化后的代价函数；pn表示帝国的势力大小；NCn为帝国n分配的殖民地数量。

对于每个帝国，从Ncol个殖民地中随机选择相应个数的殖民地分配给该帝国，最终形成初始的Nimp个帝国集团。

3.4 产生殖民地的位置

为了改善标准ICA算法的性能，引入变异和交叉操作来产生新的殖民地位置，具体步骤如下：

步骤1对于当前循环代数t的殖民地i按照式（24）向最好帝国移动得到变异位置向量Vi(t+1) 。

步骤2将变异位置向量Vi(t+1) 与殖民地所属帝国n按照式（25）进行交叉得到新的殖民地位置：

3.5 交换帝国和殖民地的位置

殖民地移动到新的位置后，如果殖民地的势力比所属帝国的势力大，则交换殖民地与所属帝国的位置。殖民地将作为新的帝国，帝国则成为殖民地。

3.6 帝国集团的势力

一个帝国集团的势力由两部分组成：帝国主义国家的势力和帝国所拥有的殖民地国家势力。帝国主义国家的势力对总势力的影响更大。一个帝国集团的总势力按照式（26）定义：

其中，TCn为帝国集团的总势力；ωi为帝国集团中殖民地的代价函数（详见2.9 节）；ξ为常数，取值为[0,1]之间的实数。

3.7 帝国集团竞争

通过竞争的方式，最弱帝国集团中的最弱殖民地将被其他帝国集团占有。每个帝国集团都可能占有最弱殖民地国家，可能性按照式（27）计算：

其中，NTCn为帝国集团n的相对代价函数，按照式（28）计算：

令向量D=P-R，其中P=[pr1,pr2,…,prNimp]，R=[r1,r2,…,rNimp]，r1,r2,…,rNimp～U( 0,1) 。D中最大元素对应的帝国集团将占有最弱的殖民地国家。

3.8 弱势帝国灭亡

在竞争中，弱势帝国的殖民地将被其他帝国瓜分，当一个帝国集团失去所有的殖民地国家时，该帝国将灭亡，该帝国会被从种群中删除。

3.9 代价函数

给定帝国主义国家或者殖民地国家，通过解码得到解(X,Y,Z)，并按式（29）计算国家的代价函数：

其中，f(X,Y,Z)为目标函数表达式（1），路径可靠性约束（2）、车辆能力约束（11）和配送中心能力约束（12）作为惩罚项加入评价函数中。α1、α2和α3为惩罚系数。(·)+表示如果括号内值为正，则取该值。

4 实验仿真与分析

为了验证模型的合理性和HICA算法的有效性，对不同的数值算例进行测试。表1给出不同算例的规模，包括配送中心数量、客户数量和车辆数量。算例的参数按照表2中均匀分布产生。算法通过Matlab编程实现，并且所有测试的实验环境为Intel Core i5 CPU 2.2 GHz，内存4 GB计算机，操作系统Windows 7。

表1 算例的规模

表2 算例的参数

首先，对不同规模算例I1～I12 进行求解来测试HICA 的性能，并将结果与标准ICA 算法及PSO 算法进行对比。其中，所有算例的可靠性水平β取值为0.5。为公平比较，HICA 算法和标准ICA 算法的初始国家数量为100，初始帝国的数量为10，最大迭代次数为100，ξ取值为0.1。HICA 算法的常数F取值为1.5，交叉概率CR取值为0.9。PSO 算法的种群规模为100，最大迭代次数为100，惯性系数为0.8，加速常数为1.6。

对于每个算例，每种算法分别运行10 次。表3 给出不同规模下HICA 算法、ICA 算法和PSO 算法的结果比较，包括最好值、最差值、平均值、平均偏差率和CPU平均运行时间。其中，平均偏差率定义为：（（平均值−最好值）/最好值）×100%。由表3可见，对于不同规模的算例，HICA 算法的最好值、最差值、平均值和平均偏差率均低于标准ICA 算法及PSO 算法。其中，HICA 算法的平均偏差率在2.4%～8.3%之间变化，而标准ICA算法的平均偏差率在9.5%～18.9%之间变化，PSO 算法的平均偏差率在8.8%～14.7%之间。可见，HICA 算法能够对不同规模的算例进行有效求解，并且随着问题规模的增大，HICA 算法仍然能够保持较好性能。此外，由于引入交叉和变异操作会增加HICA算法的运行时间，所以HICA 算法的CPU 平均运行时间略高于标准ICA算法。

表4给出算例I1～I12的详细结果，包括配送中心的开设成本、车辆的固定运营成本、运输成本、运输油耗及CO2排放成本。

为了分析可靠性水平β对算法性能和优化决策结果的影响，以算例I5 为例进行实验。其中，可靠性水平β取值为0.3～0.8。对于不同的可靠性水平，每种算法分别运行10 次。表5 给出不同可靠性下HICA 算法与标准ICA 算法的结果对比。由表5 可见，HICA 算法的平均偏差率在2.9%～7.3%之间变化，而标准ICA算法的平均偏差率在13.1%～16.9%之间。HICA 算法的最好值、最差值和平均值也都优于标准ICA算法。因此，不同的可靠性水平下HICA算法仍然能够保持性能稳定，并且求解效果优于标准ICA算法。

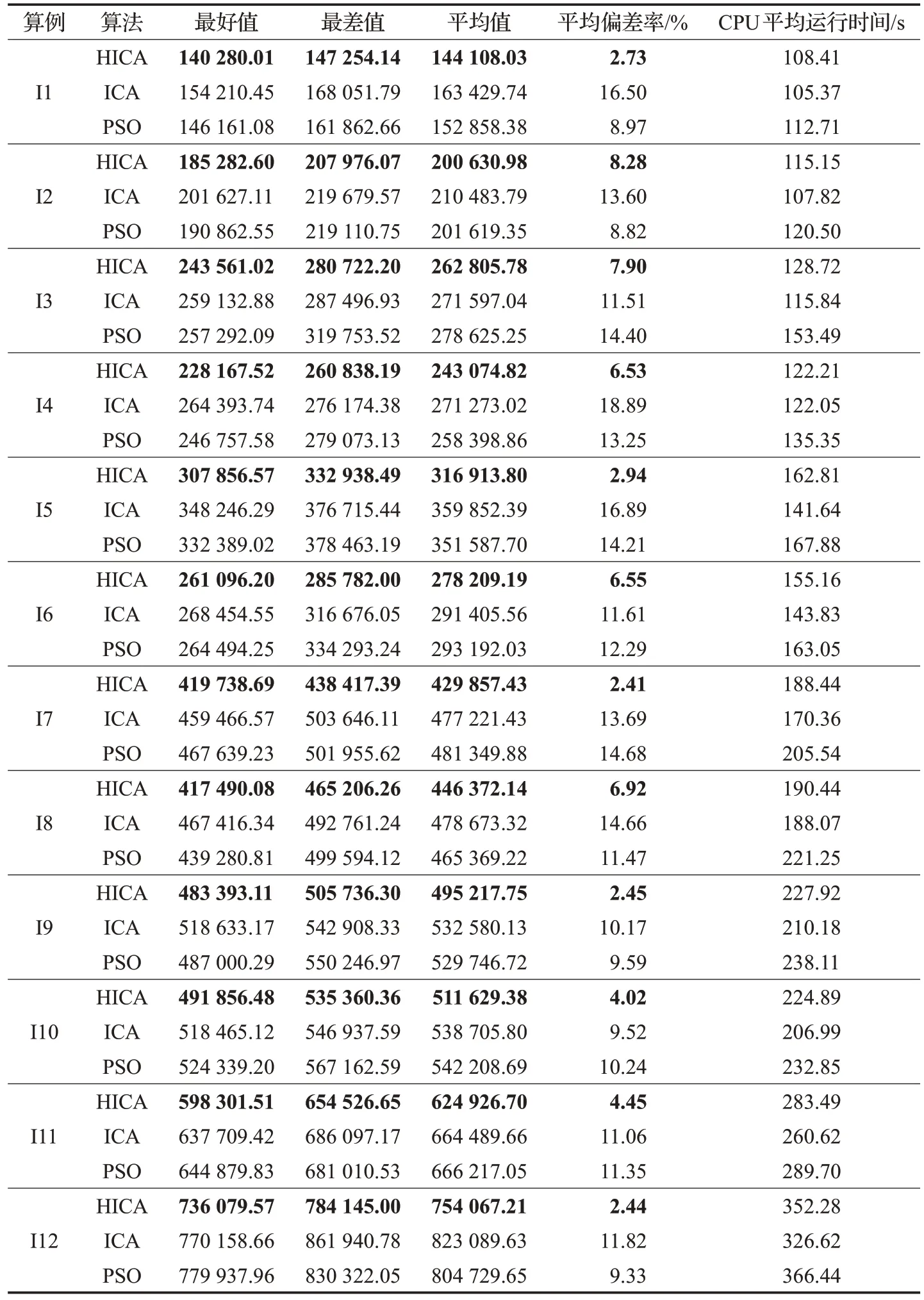
表3 不同规模算例下HICA与ICA及PSO结果对比

表4 不同规模算例的详细结果

表5 不同可靠性水平下HICA与ICA结果对比

表6 不同可靠性水平下算例I5的详细结果

表6 给出算例I5 在不同可靠性水平下的详细结果。由表6 可见，随着可靠性水平的增大，总成本和车辆的固定运营成本都单调增大，运输成本和运输油耗及CO2排放成本也呈现增大的趋势。因为，减少每个车辆经过的客户会增加车辆路径的可靠性，所以当可靠性水平增大，车辆数会增多，导致车辆的固定运营成本增加，同时也将导致总的运输距离增大，进而运输成本和运输油耗及CO2排放成本也会增大，以上成本的增大最终使总成本增大。

5 结束语

本文研究可靠性绿色物流配送选址-路径优化问题，建立了问题的优化模型，在满足路径可靠性约束的条件下最小化总成本，包括配送中心的开设成本、车辆的运营成本、运输成本及运输油耗和CO2排放成本。根据问题特点，设计了混合帝国竞争算法（HICA）。最后，通过数值算例对算法性能进行测试，并对重要参数进行分析。实验结果表明，HICA算法能够对问题有效求解，其性能优于标准ICA 算法，并且随着可靠性水平的增大，车辆数量增加，进而使车辆运营成本、运输成本、运输油耗及CO2排放成本增加，最终导致总成本增加。在未来研究中，可进一步考虑动态环境下的可靠性绿色物流配送选址-路径优化。