长江经济带工业经济效率测度及其影响因素研究
□方大春
(安徽工业大学 商学院,安徽 马鞍山243032)
一、引言
随着资源环境约束的不断加大,高投入、高消耗、偏重数量扩张的发展方式已经难以为继,长江经济带作为我国生态文明建设的先行示范带、创新驱动带、内河经济带与协调发展带,提升工业经济效率不能仅仅追求期望产出最大,忽视非期望产出,需要统筹考察期望产出和非期望产出[1](p75-83)。有些学者对长江经济带工业经济效率测度,往往基于最大期望产出传统视角。杨庆等(2018)运用DEA-Malmquist 指数法,选取物质资本、人力资本和经费投入作为投入指标,主营业收入和专利申请数产出作为产出指标,测算长江经济带高技术产业发展效率[2](p68-74)。王圣云等(2018)基于DEA 和Malmquist 指数分解方法,选取了R&D 人员数和R&D 经费内部支出作为投入指标,发明专利授权量、承担课题数作为产出指标,考察长江经济带科技创新效率[3](p66-72)。
对效率测度一般选用数据包络分析法(DEA),DEA 的效率测度以投入最少和产出最大为评价标准,但在实际生产中会出现较为明显的副产品,例如污染物排放品,也就是非期望产出。很显然,从绿色发展视角看来,非期望产出越少越能体现绿色经济效率的发展理念,然而传统的DEA 模型不能很好地处理实际生产过程的“非期望产出”[4](p103-106)。因此在处理非期望产出时,不适合直接套用传统的DEA 模型,需要对非期望产出进行转换处理。对于经济效率提升,多数学者认为需要提升技术进步,从创新投入、创新环境和创新平台等方面入手,却忽视区域产业结构对经济效率的影响,没有区域产业结构优化升级、区域间产业协同,产业技术进步难以创造经济效率。本文试图通过线性数据转换函数法将越小越好的非期望产出转化为越大越好的期望产出,然后用DEA-BCC 模型和DEA-Malmquist 指数法分别从静态和动态角度计算工业经济效率,并探究工业经济效率影响因素。
二、工业经济效率测度
(一)DEA效率测度模型
1. DEA-BCC 模型。DEA 模型(Data Envelop⁃ment Analysis)即数据包络分析法,是由运筹学家查恩斯(Charnes)等在1978 年提出的用于评价相同部门有效性的一种线性规划模型,基本模型可分为CCR 模型和BCC 模型。BCC 模型是在原始CCR 模型的基础上改进而来的,它修正了CCR 模型假定规模报酬不变的原假设,设定规模报酬可变。具体将CCR模型中的综合技术效率值(TE)进行分解为纯技术效率值(PTE)和规模效率值(SE),分解公式为:TE=SE*PTE。综合技术效率是对决策单元资源配置情况、资源利用状况等多方面的综合测定及考量,纯技术效率是受到内部管理以及技术使用影响的效率,规模效率是受规模因素影响的生产效率[5](p74-78)。引入正负偏差变量S+、S-后,可得到具有非阿基米德无穷小量ɛ的BCC模型。第j个决策单元的BCC模型表述如式(1)所示:
其中,θ 表示决策单元效率值;j=1,2,3,…,n代表决策单元的个数;X、Y 分别表示投入向量、产出向量;设定模型。
若θ = 1,S+= S-= 0 ,则表明决策单元处于DEA有效;
若θ = 1,S+≠0 或S-≠0 ,则表明决策单元处于弱DEA有效;
若θ < 1,则表明决策单元处于非DEA有效。
2.DEA- Malmquist 指数法。 采用非参数的DEA 数据包络分析法,结合Malmquist 指数法动态测度长江经济带工业全要素生产率水平。基于数据包络分析法的Malmquist指数的计算公式如下:
式(2)中,Dkt表示产出距离的函数,t表示不同的参照时期,上标k指研究范围的某个区域。将式(2)两边公式分别记为TFPch、TEFch和TEch,则区域k在某一时期内的全要素生产率可表示为:
为修复基西米河,1999年实施了基西米河生态修复工程。该工程的目标是恢复一个可以自我维持的基西米河及河漫滩生态系统,具有与历史上相同的生态功能并能支持与历史上相当的动物群、植物类型和水流特征。
式(3)中,TFPch 指在t 到t+1 时期内的全要素生产率的变动,TEFch指在t到t+1时期内的技术效率变化指数,TEch 指在t 到t+1 时期内的技术进步指数。若这三个指标大于1,代表全要素生产率、技术进步及技术效率得到改善。
(二)变量选取和数据处理
研究对象为长江经济带11 省市,研究时段为2010—2016 年。投入变量及产出变量来源于《中国统计年鉴》《中国工业统计年鉴》、各省市统计年鉴及各省市历年国民经济和社会发展统计公报整理所得。为剔除价格因素影响,以2010 年为基期对其进行平减。
1.投入变量选取。投入变量包括劳动力投入、资产投入、能源投入三个方面。劳动力投入采用规模以上工业全部从业人员数,资本投入用工业固定资产净值年平均余额表示,选取地区工业能源消费量作为能源投入的衡量指标。
2. 产出变量选取。采用双产出变量衡量长江经济带工业能源利用效率状况,包括期望产出和非期望产出。其中期望产出用工业销售产值表示;非期望产出采用工业“三废”来表示,具体包括工业废水排放总量、工业SO2排放总量以及工业固体废物排放总量。
基于传统DEA 模型投入最少越好、产出越多越好的期望,对模型中含有非期望产出的变量,需要对非期望产出进行转换。学术界比较常见的非期望产出处理方式有两种:一种是把非期望产出作为一种特别的投入变量进行研究,但是这种处理方式容易造成工业效率的测度出现偏差;第二种方法是以线性转换的形式对非期望产出进行处理,将其转换为越大越好的期望产出[6](p85-96)。参照Seiford 和Zhu(2005)对非期望产出的线性转换方法,对工业“三废”产出进行处理[7](p579-581)。设Cij为长江经济带j 省份第i 年度的“三废”排放量,max(Ci)为第i 年度长江经济带“三废”排放的最大量,取ξ= max(Ci)+ 1,则进行线性转化后的“三废”排放量为Cij*=-Cij+ξ,且Cij*≥1。通过线性转换将生产过程期望越小越好的“三废”产出转换为越大越好的期望产出,再基于DEA- BCC 模型和DEAMalmquist指数法分别从静态和动态角度测度工业效率。
(三)基于DEA的静态效率测度
利用deap2.1 分析软件,使用投入导向型的DEA- BCC 模型对长江经济带沿线11 省市2010—2016 年间的经济效率进行测度,得到静态工业效率值(crste),进一步将其分解为纯技术效率(vrste)和规模效率(scale),即crste=vrste×scale。根据历年DEA 测算结果,计算2010—2016 年各效率的平均值,结果见表1:
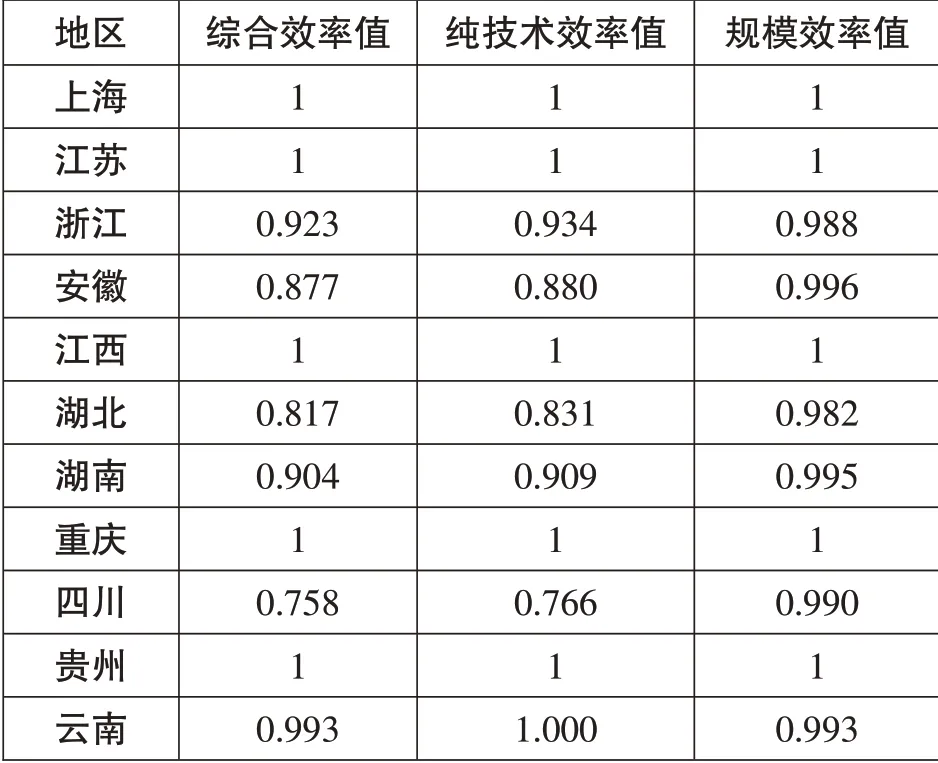
表1 长江经济带各省市2010—2016年静态效率值平均值
从表1中可以发现,上海、江苏、江西、重庆、贵州五省市七年间综合效率值、纯技术效率值及规模效率值平均值为1,处于DEA有效。在长江经济带经济效率中位于第一方阵;云南、浙江、湖南紧接其后,其综合效率值、纯技术效率值和规模效率值均大于0.9,位于第二方阵;安徽、湖北、四川位于第三方阵,安徽的综合效率值和纯技术效率值均介于0.85—0.9,湖北的综合效率值和纯技术效率值均介于0.8—0.85,四川的综合效率值排名最后,综合效率值和纯技术效率值均介于0.75—0.8,四川省应从大力加强技术创新入手提升工业效率。总体上看,长江经济带11省市规模效率接近有效,综合效率不高主要是由纯技术效率不高导致的。
(四)基于Malmquist指数的动态效率测度
DEA方法用的是每一年度的截面数据,测度的是工业生产过程中各个地区在同一时点的相对效率[8](p22-30)。为了进一步衡量跨期的动态生产效率,Fare 等人提出了考察两个相邻时期生产率变化的Malmquist 生产力变动指数方法[9](p66-83)。Malmquist是对包含时间变量的面板数据进行动态分析,测度投入产出效率的变化,可分解为效率改进指数(effch)和技术进步指数(techch),而效率改进指数(effch)可进一步分解为纯技术效率变化指数(pech)和规模效率变化指数(sech),即:Malmquist=effch×techch,effch=pech×sech。运用软件deap2.1 测度2010—2016年效率变动情况,结果见表2:
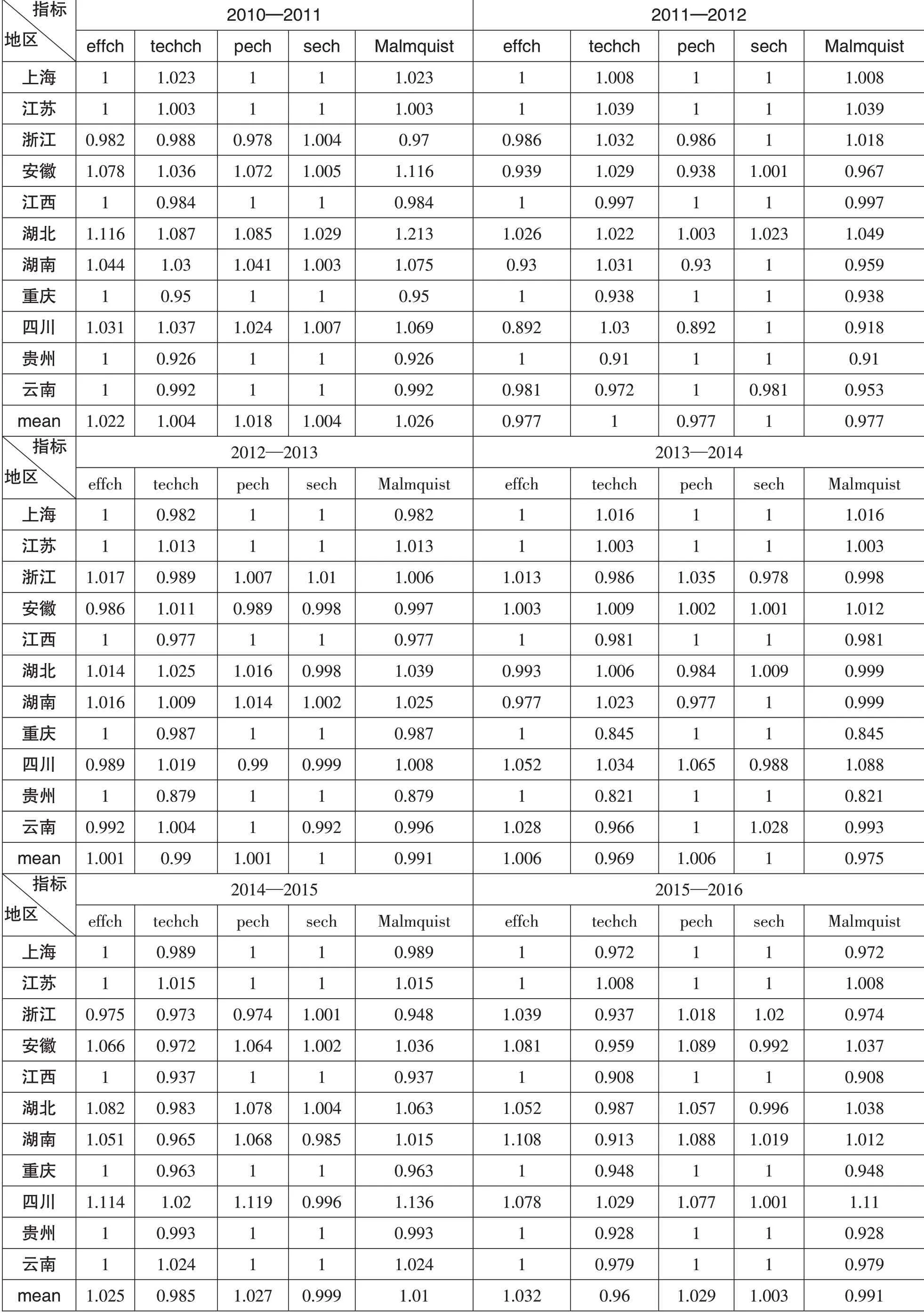
表2 2010—2016年长江经济带11省市Malmquist指数及其分解
由表1 可以看出:长江经济带2010—2016 年间Malmquist 指 数 分 别 为1.026、0.977、0.991、0.975、1.01、0.991,除2010—2011 年和2014—2015年,其他年份Malmquist 指数均小于1,这表明工业经济效率呈下降态势。
分地区来看:江苏在2010—2016 年间Malmquist 指数均大于1,其中效率改进指数均为1,工业效率驱动力主要来自技术进步。湖北和四川有五年Malmquist 指数增长率大于1,工业效率整体上处于不断增长中;湖北受效率改进影响较大,在影响效率改进的因素中,纯技术效率改进的影响较大;四川工业效率的提高来自技术进步和效率改进双重动力。安徽和湖南有4年Malmquist指数增长率大于1,两省份效率的增长均主要受效率改进的影响,且在影响效率改进的因素中,纯技术效率改进占更大的影响比重。上海2010—2016年间的Malmquist 指数分别为1.023、1.008、0.982、1.016、0.989、0.972,上海的效率改进指数七年间均为1,工业效率不断下降主要受技术改进的影响。浙江只有两年Malmquist 指数增长率大于1,工业整体增长率不高是技术进步和效率改进双重低下导致的。云南和贵州仅有一年Malmquist指数增长率大于1,两省份效率改进均接近有效,工业效率不高主要原因在于技术进步动力不足。江西和重庆七年间Malmquist 指数增长率均小于1,其中效率改进指数在七年间均为1,工业效率不高主要受技术进步的影响。
长江经济带11省市七年间Malmquist 指数、技术进步指数和效率改进指数平均值对比见图1。
从图1 可以看出,长江经济带Malmquist 指数年平均增长大于1 的省份有七个,分别为湖北、四川、安徽、湖南、上海、江苏、云南。中游地区Malmquist 指数平均值较高,除江西外其他省份Malmquist 指数平均值均大于1;下游地区次之,除浙江外其他省份Malmquist 指数平均值均大于1;上游地区最差,重庆、贵州Malmquist指数平均值均小于1,贵州甚至低于0.95。
总体上看,11省市效率改进指数(effch)均在1及1以上,工业效率受技术进步(techch)影响较大,这表明长江经济带提升工业效率的重点在于提高工业技术进步。
三、工业效率提升产业结构影响因素实证分析
根据前面Malmquist 指数及其分解可知,长江经济带提升工业效率的重点在于提高工业技术进步。工业技术进步的提升,一般认为要从加大技术研发投入、技术成果转化力度和加快机制体制创新等方面入手。实际上,工业技术进步需要从产业结构优化入手。如果地区产业结构处于低层次,没有产业载体难以加大技术投入;如果地区产业结构不够合理,导致技术研发投入效果不显著;地区产业专业化程度过低,难以产生规模效率,专业化程度过高,也会产生规模不经济。地区产业结构优化,不仅能够提高地区工业效率,也能为长江经济带产业合理布局提供参考。
从前面研究结果来看,无论静态效率还是动态效率,长江经济带各地区工业效率均存在很大差距,且部分省市效率值呈现逐年恶化的趋势。试图从产业结构角度,考察长江经济带工业效率的影响因素,为各省市工业高效率发展提供改进方向。
(一)变量选取及数据处理
分别以Malmquist 生产率增长指数、效率改进指数(effch)和技术进步指数(tech)的累计值为因变量。各主要解释变量具体含义如下:
1. 工业产业高级化(TS)。 参考傅元海等(2014)的做法,利用高技术产业产值占工业总产值之比来衡量工业产业结构高级化[10](p78-90)。高技术产业包括医药制造业、航空航天器及设备制造业、电子及通信设备制造业、计算机及办公设备制造业、仪器仪表制造业及信息化学品制造业。
2.工业产业专业化(SP)。以产业偏离度来衡量地区产业专业化程度,当产业偏离度值越大时,表明该产业在经济体中占绝对优势,专业化程度越高,具体公式如下[11](p55-62):
其中,Q 表示工业总产值,L 表示工业从业人员数,i表示工业行业,N表示行业部门数。Qi表示工业第i 行业的产值,Li表示工业第i 行业的就业人数。
3.工业产业合理化(SE)。长江经济带产业布局最为突出的问题就是产业趋同的问题,借鉴王林梅等(2015)的做法[12](p39-43),采用产业结构相似系数测度各地区产业布局在长江经济带内的产业同构现象,具体公式如下:
其中,Sij代表i 和j 两地区产业结构的相似系数,在这里地区j代指长江经济带内除地区之外其他地区,Sij代指各省市与长江经济带其他地区布局的同构化程度。Xik和Xjk则代表地区i、地区j中k行业所占的份额。其中Sij值介于0—1。Sij系数越大,则代表i 地区和j 地区产业结构布局越相似。若Sij=1,则表明i 地区和j 地区的产业结构完全相同;若Sij=0,则表示i 地区和j 地区产业结构相似程度为零。
4. 其他影响因素(Xit)。除列出的产业结构解释变量外,工业经济效率还受到很多因素的影响,考虑投入规模经济和技术引进两大主要影响因素,需要把科技发展水平(TM)以及经济开放度(TO)纳入模型。其中经济开放度以各省市出口商品总额占GDP 比重作为度量指标,科技发展水平选取各省市技术市场成交额占GDP的比重作为测度指标。
(二)模型设定
分别构建Malmquist 生产率增长指数、效率改进指数(effch)和技术进步指数(techch)影响因素模型。
其中,i 表示省区截面单元,i=1,2,…,30;t 表示时间;Malmquistit、Effchit、Techchit分别为被解释变量;TS和SP分别表示工业产业结构高级化和专业化;SE为产业结构合理化;X为其他影响因素。
(三)结果分析
在模型估计的选择上,先对模型做Hausman检验,得出结果拒绝随机效应模型与固定效应模型系数无系统性差异的假设,故选择固定效应模型来进行回归分析,结果见表3。模型1、模型3和模型5 分别为各主要解释变量对Malmquist 指数、效率改进指数和技术进步指数的回归结果。模型2、模型4和模型6是加入控制变量后的回归结果。
从模型1、模型3、模型5 的结果来看,产业高级化对Malmquist 指数、效率改进指数和技术进步指数分别在1%、10%和5%的显著性水平下产生正向影响,这表明现阶段工业产业结构升级,有利于提高工业整体运行效率,且对技术进步和效率改进两个方面均有正向影响。长江经济带应抓住信息技术革命、经济服务化的历史机遇全面推动工业产业结构高度化(滕堂伟,2016)[13](p92-99)。
产业专业化对Malmquist指数及技术进步指数有正向显著影响,对效率改进影响不显著。这表明地区产业布局不能盲目追求多样化,要注重产业的专业化布局,当经济发展到一定程度时,多样化会造成地区有限的资源被过度分散,反而可能会起抑制作用。各地区应该依据自身经济发展水平设计和调整产业格局,充分发挥本地经济的优势,鼓励专业化分工,实现地区间的合理分工协作。

表3 工业效率影响因素分析
产业合理化指标是负向指标,产业结构合理化系数在模型中表现为负数,表示产业同构对Malmquist 指数、效率改进指数和技术进步指数有显著抑制作用,也就是产业结构合理化对其表现为促进作用。推进长江经济带工业高质量发展,不仅要提高产业布局的高级化、专业化,也要关注区域间产业布局的合理性,不能盲目追求产业的高级化,要减少区域产业布局的同构性。
加入控制变量后,各主要解释变量的正负号及显著性未发生明显变化,这表明模型具有一定的稳健性。技术市场成交额分别在1%的显著性水平及5%的显著性水平下促进Malmquist指数、效率改进指数和技术进步指数的增长,技术市场的成交额是衡量地区产业资源配置、科技创新以及成果转化的重要衡量指标[14](p1471-1478),因此提高工业效率要注重对科学技术的引进、吸收及转化;经济开放度对各主要被解释变量的影响不一,对Malmquist指数、效率改进指数有负向影响,对技术进步指数影响不显著,这和长江经济带本身对外开放程度不高有一定的关系。
四、结论与建议
从静态和动态角度测度长江经济带11个省市工业经济效率,再从产业结构视角探究工业经济效率影响因素,研究结论如下:第一,从静态效率来看,长江经济带经济效率非有效地区主要集中在长江上游地区,综合技术非有效主要是纯技术效率和规模效率非有效共同导致的,但纯技术效率对综合技术效率的影响高于纯技术效率的影响。第二,从动态效率来看,工业效率增长的主要驱动力量源自技术进步。分区域来看,长江中游地区工业效率较高,下游地区次之,上游地区最差,主要受技术进步影响较大。第三,从工业效率的影响因素来看,产业高级化及产业专业化对工业效率有正向显著影响,产业趋同对工业效率起显著抑制作用,这表明现阶段要合理规划长江经济带产业布局,避免产业趋同,各地区应发挥地区经济的特色和优势,鼓励专业化分工,实现地区间合理分工协作。
基于实证分析,需要从以下几个方面,提升长江经济带工业效率:首先,在提高投入规模基础上推进技术进步。推进技术进步,加大技术转化力度,提高技术对工业经济发展的贡献率,共同促进经济效率提升。其次,要调整工业产业结构。当前产业结构高级化和合理化对工业效率的提升均起显著正向作用,因此在对各地区进行产业布局时,一方面要选取具有发展潜力的产业作为重点布局对象,另一方面也要从全局出发,促进各地区优势互补、协同发展。最后,要提高工业专业化水平。当前长江经济带工业产业多样化进入到一个新时期,盲目布局多种产业没有起到拉动工业经济的作用,反而加重了工业经济的负担。要坚持“一盘棋”战略思维,各个地区从整体出发,避免进行同质化竞争。因此,各地区在进行工业产业布局时要整合区域内部资源及自身优势,制定具有地方特色的产业发展战略,更好地推动工业高效率发展。

