一种星载GNSS-R海面风向反演方法

高 涵，白照广，范东栋

(航天东方红卫星有限公司，北京 100094)

0 引 言

海面风场是海洋上层运动的主要动力来源,也是研究大气和海洋之间热量交换和物质交换的重要因素，是研究海洋动力过程的重要要素[1]，全球导航卫星反射信号技术(Global navigation satellite system reflections，GNSS-R)是近年来兴起的新型遥感手段，该技术利用导航卫星L波段信号的反射信号作为遥感源，信号来源丰富[2]，具有全天时、全天候遥感的能力，尤其是星载GNSS-R系统，在海面风场探测、海冰探测、海洋溢油探测等方面有着突出的应用效果[3-5]。

海面风场反演主要分为海面风向反演和海面风速反演，其中海面风向反演是风场反演中的难点。文献[6]中提出利用海面坡度进行风向反演，利用特征向量法，在接收机高度为3～5 km情况下，筛选数据后进行反演，获取风向反演精度最高为5°，未经筛选的数据风向反演精度降低为40°。文献[7]中提出时延曲线后沿斜率与风向存在一定相关关系，通过延长积分时的方式扩大这种相关关系，反演结果存在180°模糊。文献[8-10]默认海面均方坡度概率密度函数(Probability density function of the surface slopes, PDF)为各项同性，用两颗不同方位角的卫星进行风向反演。文献[11]建立了基于NOAA G-IV jet aircraft机载风向反演模型，利用时延多普勒相关功率图(Delay doppler map, DDM)上多普勒维的偏移角作为反演观测量，在固定模型下获取风向反演平均精度为20°，但其基于机载数据数据量较小且模型为特定模型非通用模型，存在180°模糊。通过以上可以看出传统的GNSS-R海面风场反演中，风向反演方法较为匮乏，缺乏大面积海面风场反演方法。基于神经网络的反演技术近年在海面风场反演中得到应用，冯倩等[12]提出基于混合密度网络的海面风场反演方法，利用神经网络的自适应和自学习能力，从散射计数据中提取反演风场所需信息，以NSCAT散射计数据为例证明了该方法的有效性。陈坤堂等[13]提出基于BP网络的HY-2微波散射计数据反演方法，获取的反演数据可以满足风向反演一般精度要求。文献[14]利用神经网络反演了海面风速，但采用单层神经网络，未能提取更深层的风向关系，无法反演海面风向信息。

本文提出了一种基于GNSS-R数据的海面风向反演方法。首先根据反演目标特征确定了反演观测量，然后建立了神经网络模型并优化网络结构。模型的训练学习采用CYGNSS卫星数据和ECMWF融合风场数据。最后通过试验校验了反演方法的有效性和鲁棒性。

1 星载GNSS-R风向反演观测量

利用神经网络反演海面风向，需要提供输入数据和与之对应的输出风向，通过神经网络自学习过程建立反演模型，首先选择星载GNSS-R风向相关观测要素作为反演观测量输入，本文选择的4个观测量分别为海面均方坡度概率密度函数(Probability density function，PDF)，海面风速，时延相关曲线后沿斜率(Trailing edge slope，TES)和卫星高度角。

1.1 海面均方坡度概率密度函数

海面风场引起海表面高低起伏变化，在风场作用下，海洋表面各点的均方斜率呈现不同的分布状态，该状态可以由海面均方坡度的概率密度函数描述[15]。其表达形式为

(1)

(2)

式中:k为波数，由海面风速决定，θ为海面风向，ψ(k,θ)为二维海浪谱函数[16]。由式(1～2)可以得知，FPDF是海面风速与主风向的调和函数，在确定风速的情况下，风向可以由FPDF反演得到。

根据卫星获取的GNSS-R观测量，可以由KA-GO方法[17]计算海面均方坡度概率密度函数

(3)

式中：σ0(τ,f)为归一化散射截面系数[17]，是GNSS-R直接观测量，R为菲涅尔反射系数，用于校正海面均方坡度。

R(θ)=

(4)

式中：ε为海水介电常数，θ为卫星高度角。

(5)

式中：φ为散射区域内任意点P相对镜面点的方位角，θ1和θ2为P点处的入射角和散射角。如图1所示。

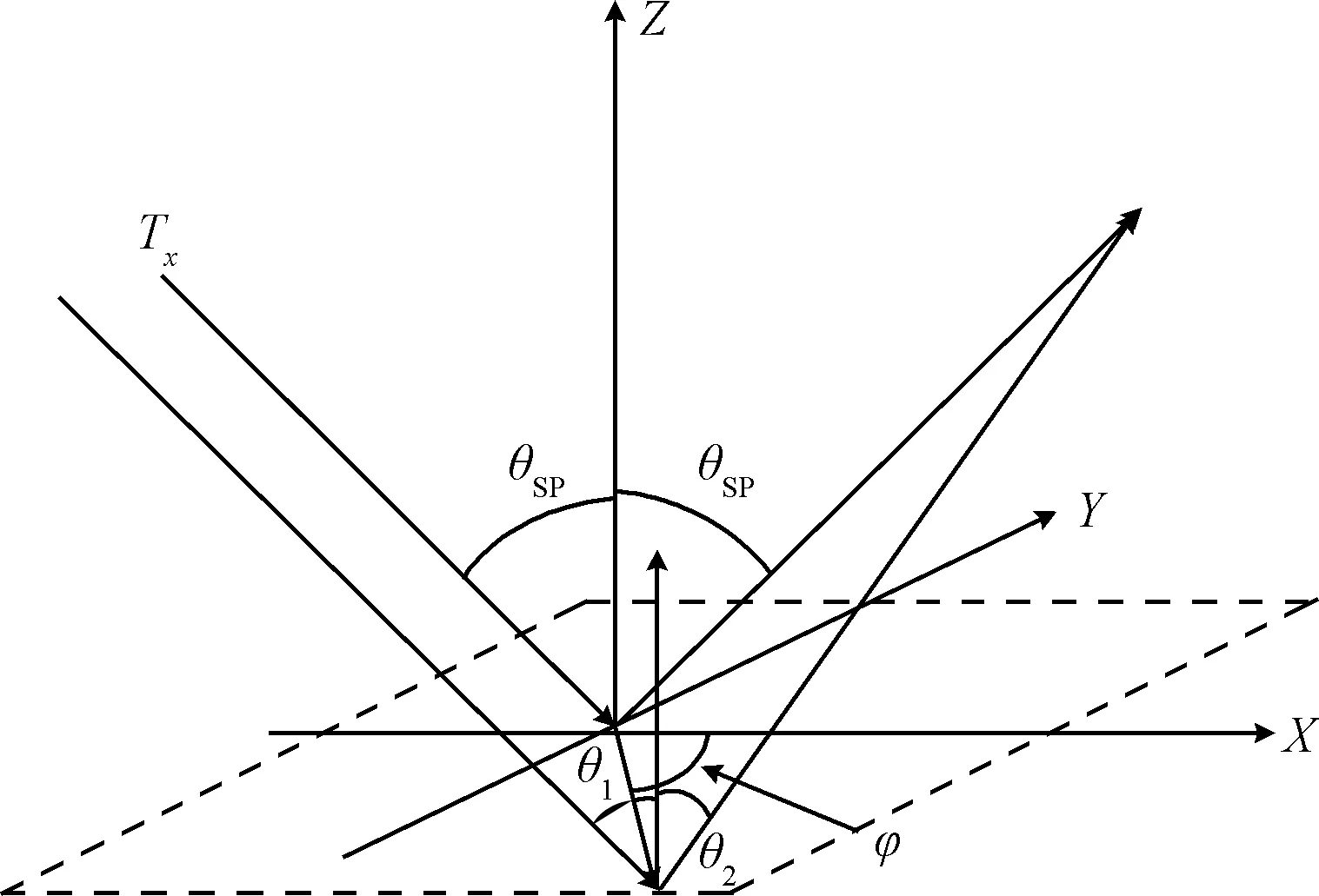
图1 准镜面散射几何关系图

1.2 时延相关曲线后沿斜率

时延相关曲线后沿斜率描述了散射信号在时延维上的强度分布情况，其分布值受风向和卫星高度角影响，在顺风向时比侧风向时相关功率拖尾更长，斜率更大。在卫星高度角60°，风速8 m/s时不同风向下散射信号功率波形如图2所示，k1,k2,k3分别表示分别表示顺风向夹角30°、60°和90°时，时延相关曲线后沿斜率的变化情况，风向偏离顺风向越多，斜率越小，即k1>k2>k3。根据这一特征，可以由时延相关曲线后沿斜率反演海面风向。

图2 不同风向下时延相关曲线TES

1.3 卫星高度角

卫星高度角影响GNSS-R散射区域分布情况，高度角变化，影响时延相关曲线后沿斜率[18]，影响风向反演结果。如图3所示，卫星高度角增加，时延功率曲线拖尾变长，后沿斜率变小，这种现象在高度角越低时越为明显。如图3是在风速10 m/s，风向为0°时卫星时延相关曲线。

图3 不同卫星高度角下一维时延功率曲线

2 海面风向反演网络模型

深度神经网络是多隐藏层的神经网络，由于隐藏层数较深，后面层网络可以在前面层网络学习到的初步特征基础上形成更高级别的特征[19]，由于风向反演中观测量与风向之间的特征关系复杂，采用深度网络可以更好的建立对应关系，反演风向信息。建立如图4的深度网络模型，图4中X1,X2,X3,X4为网络的输入观测量，f1,f2,…,fn+t+1均为激活函数，输出量为风向。

图4 深度神经网络拓扑

2.1 激活函数选择

激活函数是在神经元中，输入量经过加权，求和后进入下级前输入的函数，在深度神经网络模型，如卷积神经网络(Convolutional neural network，CNN)中，与反演量相关的数据特征有限，但深度模型中网络连接数量巨大，造成反演参数特征挖掘的效率和精度下降，因此需要选择合适的激活函数，增强模型稀疏性。

修正线性单元(Rectified linear unit，ReLU)函数形式为

(6)

ReLU函数具有单侧抑制特性，把所有的负值都变为0，而正值不变，当模型增加N层之后，理论上ReLU函数神经元的激活率将降低2的N次方倍[20]本文采用深度网络反演风向信息，采用ReLU函数实现稀疏后的深度网络模型能够更好地挖掘风向相关特征，拟合训练数据。

2.2 GA算法优化网络结构

采用深度网络建立反演模型时，网络初始权值会影响反演结果，传统BP网络学习过程中隐含层节点数与权值难以选取，引起网络收敛缓慢，易陷入局部最优。遗传算法(Genetic algorithm, GA)是一种通过模拟自然进化过程搜索最优解的方法，具有很强的宏观搜索能力和良好的全局优化性能。利用遗传算法的全局搜索能力优化神经网络的权值和阈值，可以获取最优的网络结构，提高反演精度[21-22]。

2.2.1确定网络隐含层节点数

神经网络隐含层节点数的选择目前没有确定的理论和方法，本文采用了4层深度网络，隐层节点数采用三分法确定[23]，首先确定隐层节点数范围

(7)

本刊已加入《国家哲学社会科学学术期刊数据库》《中国学术期刊（光盘版）》《中国期刊网》《万方数据——数字化期刊群》《中文科技期刊》全文数据库，以及超星数字期刊。若作者不同意将文章入编上述数据库，请在投稿时加以说明，本刊将作适当处理。本刊作者文章著作权使用费、稿酬与版面费相抵，编辑部不额外收费，不另付酬。

(8)

式中：n为输入层节点数；m为输出层节点数；a为整数，且1≤a≤10。

图5 隐含层节点数计算流程图

2.2.2优化网络权值与阈值

采用遗传算法优化网络权值和阈值主要分为神经网络训练拟合与遗传算法极值寻优两部分。算法流程如图6所示。

图6 GA优化深度网络流程图

将训练后的神经网络预测结果作为个体适应度值，并通过选择、交叉和变异操作寻取函数全局最优值作为神经网络的初始权值和阈值。

3 数据预处理

利用深度网络反演需要从大量不同的待训练数据中提取特征数据。为避免由于输入数据质量特性影响网络泛化能力或引起反演误差。需要对反演输入数据进行预处理。数据的预处理主要分为数据的时空匹配、数据预选及数据归一化三部分。

3.1 数据时空匹配

本文使用的训练数据源是CYGNSS卫星L1级数据。真值数据是欧洲中尺度天气中心(ECMWF)的海面风场融合数据。

ECMWF提供空间分辨率0.25°×0.25°[24]风场数据，CYGNSS单星每秒生成4组反演特征数据，单星平均空间分辨率0.082°×0.082°，CYGNSS数据中存在大量共反演点的数据，会形成数据冗余，为保证数据单一性同时又可以满足星下点尽可能多的覆盖率，需要对CYGNSS数据和ECMWF数据筛选和时空匹配，选择反演区域中信噪比最强的反演点观测量P作为输入数据。

P=max{10lg(Smax/Navg)}SSP

(9)

3.2 数据预选

为保证在各个风速段下风向反演的泛化能力，需要对匹配后的数据进行预选，对输入数据集共864 000组观测量及与之对应的风速数据按风速段分类，如表1所示。

表1 数据预选列表

以数据比例最低的风速高于20 m/s的数据作为采样标准，对该段风速进行全采样，对其余2个区间风速随机采样，使3个风速段的数据量相同。预选后风向数据分布如图7所示。

图7 风向数据分布

3.3 数据归一化处理

数据归一化能提高神经网络梯度下降的求解速度，并消除量纲影响。本文采用离差标准化方法对海面均方坡度概率密度函数、海面风速、DDM后沿斜率、GNSS-R卫星高度角等4个输入变量进行归一化处理，设第i个输入变量Pi=[pi1,pi2,pi3,pi4](i=1,2,3,4)，对第j个变量的离差标准化公式为

(10)

式中：max(Pi)表示第i个输入变量的最大值，min(Pi)表示第i个输入变量的最小值。

4 风向反演模型试验

建立如图4所示神经网络模型，文中采用数据集来源于CYGNSS-01星和ECMWF的融合风速数据，数据集信息见表2。

表2 数据集信息

4.1 海面风向反演流程

数据集中包括海面均方坡度概率密度函数、后沿斜率、卫星高度角、海面风速、海面风向等共5维数据，样本规模为864000个。风向反演步骤如下：

步骤1提取星载GNSS-R接收数据中与海面风向相关的观测量，以ECMWF的风向数据作为真实值，经过数据时空匹配和预选，建立反演数据集。

步骤2采用2.2.1中和2.2.2中的方法确定网络隐含层节点数，得到GA算法优化后的权值和阈值。训练网络，将网络输出风向与真值对比，计算反演精度，当精度或循环次数达到预设要求结束训练，得到风向反演的网络模型。

步骤3将验证集中的数据输入到训练好的网络中，计算反演精度，若精度达到模型预设要求，进入下一步骤，否则返回步骤2。

步骤4将测试集中目标观测值输入到训练好的网络模型中，计算风向反演精度，评价反演效果。

步骤5输入未知风向区域GNSS-R观测量，利用训练好的模型反演该区域海面风向，检验算法鲁棒性。

4.2 风向反演结果与模型鲁棒性检验

经2.2.1确定神经网络隐含层节点数为隐含层1和隐含层2均为9个节点。采用GA算法优化网络权值和阈值，网络适应度在32代后趋于稳定，适应度曲线如图8所示。

图8 GA算法适应度曲线

将训练数据输入深度网络，网络的训练次数设置为200次。误差在训练过程中逐渐减少，迭代46次后收敛。在输入数据集中随机选取验证集400个数据，试验结果如图9所示。本文方法反演的风向和ECMWF风向的相关系数为0.9588，风向反演的均方根误差εRMSE=18.14°。

图9 风向反演试验结果

为验证反演方法的鲁棒性，选取CYGNSS-01星在2018年5月15日00:00:00至2018年5月16日23:59:59与2018年5月27日00:00:00至2018年5月28日23:59:59两段时间内的L1级数据和对应真值数据两组各2000个进行验证。如图10(a)所示第1组数据使用本文方法反演的风向和ECMWF风向的相关系数为0.9441，均方根误差εRMSE=18.22°；如图10(b)所示，第2组数据使用本文方法反演的风向和ECMWF风向的相关系数为0.9386，均方根误差εRMSE=18.51°。满足海面风向测量均方误差小于20°的一般测量要求。

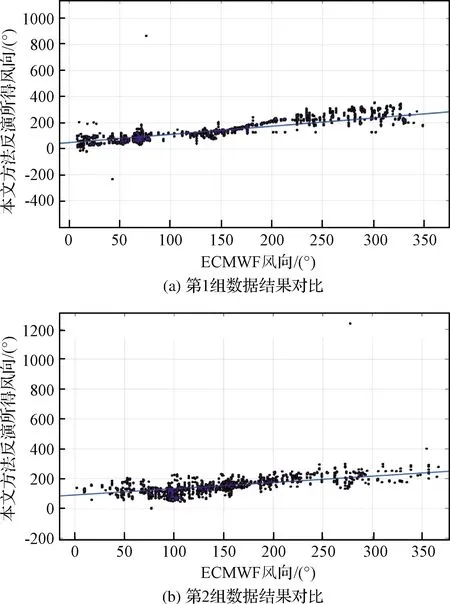
图10 深度网络风向反演验证试验结果

5 结 论

1)本文通过对星载GNSS-R观测量的分析与试验得到了多个观测量与风向间相关关系，提出了利用深度网络模型反演海面风向的方法。为海面风向反演提供了新思路。

2)设计了反演网络模型，确定网络节点数，并基于GA算法优化了网络结构，采用ReLU函数作为网络激活函数优化网络学习速度，使得网络模型可以高效准确的反演海面风向。

3)对数据进行预处理优化了网络输入条件，提高了网络的泛化能力，通过验证试验证明了该反演方法的有效性和鲁棒性。