平台型物流企业多产品运输经济分析与成本优化

梁喜 赵棒

【摘要】为实现平台型物流企业降本增效， 利用交通运输经济学中的规模经济理论、密度经济理论及网络经济理论对企业多产品运输时的运输经济进行分析并构建相应的成本优化模型。 为验证模型的有效性， 选用某平台型物流企业的运输数据、业务片区成本数据和物流运输网络数据对模型进行实例论证。 研究表明：规模经济模型可以确定多产品运输下企业总体及特定产品生产、服务规模的合理性、经济性， 为企业是否采取专业化生产提高主要产品的产出水平提供依据， 对企业确定宏观成本优化方向具有指导性; 密度经济模型通过比对企业多产品运输的理论成本与实际成本， 对企业业务片区内不同产品的运输成本控制进行指导; 网络经济模型对物流网络进行均衡优化， 其优化程度越高， 物流运输网络的效率与成本经济性越高。

【关键词】交通运输经济;密度经济理论;网络经济理论;成本优化;降本增效

【中图分类号】F274      【文献标识码】A      【文章编号】1004-0994（2020）22-0061-5

一、引言

随着社会经济和行业的发展， 产业集聚化、物流资本退潮、企业战略升级使物流企业的运营成本节节攀升。 对于具有多产品运输业务的平台型物流企业而言， 如何实现企业健康发展、如何保证多产品运输过程中的规模经济性、采取何种措施实现降本增效是亟待解决的难题。

目前国内外学者在物流企业成本优化问题上已形成较多研究成果。 国外学者如Nam等[1] 和Minken等[2] 分别使用多目标优化模型、经济订购量模型研究物流企业的成本优化， 为企业实现降本增效提供了理论参考。 国内学者如蒋丽芹等[3] 、郑尔璇等[4] 探讨了作业成本法在物流企业成本管理、控制中的作用; 姚源果等[5] 和胡元等[6] 分别运用配送路径优化数学模型、多式联运路线优化方案， 研究物流配送路径对运输成本的影响。

国内外学者在研究如何有效降低物流企业营运成本时， 主要使用决策优化模型、财务分析方法， 很少使用运输经济方法， 且目前研究均将多产品转化为单产品来处理， 在研究时都只考虑了企业的“总产出”， 但由于各个产品间的完全转化缺少折合标准， “总产出”折算存在主观性， 所以不能反映实际情况下多产品组合带来的变化对规模经济的影响。 在现实中， 平台型物流企业一般都会运输两种或两种以上的产品， 本文利用交通运输经济学中的规模经济模型、密度经济模型对平台型物流企业多产品运输情况下的经济规模性、密度经济性进行分析， 建立网络经济模型对运输线网、节点进行优化， 实现运输降本。

二、基于运输经济分析方法的平台型物流企业运输成本优化模型

物流作业涉及大量交通运输与经济活动， 因此在构建降本模型时需要综合考虑各个方面的影响因素。 本文选择交通运输经济学中的规模经济、密度经济和网络经济模型， 搭建平台型物流企业垂直降本模型， 如图所示， 该模型不仅能够让平台型物流企业实现对物流成本的宏观把控、中观实施， 而且能深入到具体物流作业过程中， 实现微观优化。

1. 规模经济模型。 规模经济模型要求经营者从宏观整体上把控企业的生产成本， 基于生产成本的变化过程对企业的生产、经营状况进行评估， 之后通过分析企业生产、服务规模的合理性， 确定企业生产的最优业务量与物流作业过程的最优成本值， 从宏观决策上实现物流企业的降本增效。 本文考虑物流企业生产产品、运输产品的多样性， 定义多产品生产企业的总体规模经济模型， 该模型能够反映不同产品对企业规模经济的影响， 能够更好地反映现实物流企业经营状况。 本文假设各投入要素价格不变， 则多产出情况下的成本函数将退化为多产出成本曲线， 基于此， 构建两种产出情况下的规模经济模型M1， 其判断式为：

其中：Q1、Q2分别为平台型物流企业A、B产品的物流运输量， a、b、c、d、e、f表示成本函数的相关系数， MC表示企业生产边际成本， Escale（Q）表示物流企业总体规模经济系数; Escale（Qi）表示特定产品的規模经济系数， 特定产品规模经济衡量的是在其他产出不变情况下， 某一种产出的变化对成本的影响， AIC表示平均增加成本， IC（Qi）为其他产出保持不变时生产特定产品i所增加的成本。

2. 密度经济模型。 根据密度经济理论， 平台型物流企业成本下降可以通过增加现有资源的使用频率来实现。 平台型物流企业在运输决策制定及产品运输过程中， 不仅希望实现同一运输工具、运输线网使用率的最大化， 而且会根据目的地距离、目的地区域内的交通运输方式等构建不同的复合运输模式， 为制定合理的降本方法， 需要在降本空间中利用现有运输的时间价值对各区域内不同产品运输的经济性进行评估。 因此， 本文构建M2密度经济模型， 其判断式如下：

其中：C1、C2、C3表示公路、铁路、水路的计算成本， TC、TTC为成本构成项， Q表示公路、铁路、水路的货物运输量， P表示单位货物所对应的运价， L表示公路、铁路、水路运输对应的平均里程， α表示时间价值， T表示平均运输时间， TFC表示总固定成本， TVC表示总可变成本， R表示预期利润和税金， C表示实际成本， Kd表示密度经济指标系数。

上述时间价值α用来度量样本企业的公路运输成本， 其构成包括驾驶人员开支、车辆油耗造成的直接成本、运输过程中由于不可抗力造成的延误成本以及产品在运输过程中因货物损坏造成的货损成本， 能够反映平台型物流企业公路运输经济性， 时间价值构成为：

其中：αw代表驾驶人员平均时薪; αe代表车辆运行过程中的平均小时磨损维修费用折算成本; αf代表公路小时平均油耗折算成本; αd为企业小时运行延误成本; αm为企业产品运输小时货损成本。

其中：Ne代表样本企业除运输人员外的职工数量， W为样本企业除运输人员外其他职工的平均薪酬， Nc为样本企业公路运输车辆数， γ代表平均货损率， λ代表单位货物的平均价值。

3. 网络经济模型。 对于平台型物流企业而言， 不同的运输线路、搭载不同的货物， 导致的成本构成也有所不同， 本文采用泛化网络， 对所有物流网络， 以运输均衡量和运输时间作为优化目标实现网络的经济性， 为企业的运输网络微观优化提供指导， 以此达到降本的效果。 本文使用M3网络经济模型， 构建如下判断式：

其中：Vm表示起讫点OD需求; δrm=1表示r路径流量; δrm=1表示路段l在路径r上; dm（Vm）表示价格与成本的逆需求函数; Vr表示货物运输的路径需求。

在物流运输过程中， 公路运输的顺畅度能够在很大程度上反映物流网络中的公路运输成本， 因此在网络经济模型中选择BPR阻抗函数作为成本函数， BPR阻抗函数如下：

其中：t0表示自由流行驶时间， Q表示实际单位小时流量， C表示道路设计最大小时通行能力， α和β为模型待定参数。 根据实际标定， 本文取α=2.62， β=4。

三、实证与应用

1. 样本来源与数据选取。 本文选取某平台型物流企业近六年的全部运输及财务相关数据。 在检验模型M1时， 以样本物流公司2013 ～ 2018年A、B两种产品的运输量及运输成本数据为基础; 在检验M2时， 选择各业务区域内两种产品运输的实际数据进行计算分析; 在检验模型M3时， 以样本物流公司现有的物流网络实际情况为基础， 对其进行线网优化。

2. 规模经济判断模型。 样本物流公司2013 ～ 2018年A、B两种产品的业务运输量与业务成本如表1所示。

在规模经济判断模型下利用Matlab对近六年的外包业务量及其成本进行拟合， 得到业务成本C的拟合函数和R-square值：

R-square确定系数是通过数据的变化来表征函数拟合的效果， 取值范围为[0，1]， 其值越接近1， 表明函数的拟合效果越好、越能反映实际情况。 业务成本的确定系数的值为0.9904， 说明业务成本的拟合函数符合数据要求。 由此计算A、B两产品的业务边际成本及物流企业总体规模经济系数。

物流企业总体规模经济系数Escale（Q）<1时， 说明企业运输A、B两种产品的总体规模已经超过了最优节点， 此时通过调整单一产品或两种产品的规模不但不会实现真正的降本增效， 反而会导致物流成本增加。 Escale（Q）>1则表明企业总体规模未达到最优节点， 物流企业可以通过扩大单个产品生产规模或同时扩大产品的生产与作业规模等措施来降低物流成本。

以样本企业六年作业与成本数据拟合结果Escale（Q）和Escale（Qi）， 得到A、B两种产品的最佳规模经济运量。 Q1≈137.29万台/年、Q2≈124.68万台/年， 与近六年样本企业业务数据进行对比， 结果如表2所示。

从表2可见， 在2014 ～ 2016年， 企业快速拓展业务， 企业运输业务量逐年增加， 导致作业成本不断增加， 在2017年企业实施降本措施之前， A、B两种产品都很难达到规模经济， 2017年企业通过控制生产、作业规模及线网优化等降本措施， 使两种产品在2018年均实现了规模经济性， 模型指标的适用性得到了样本企业实际业务数据的支持。

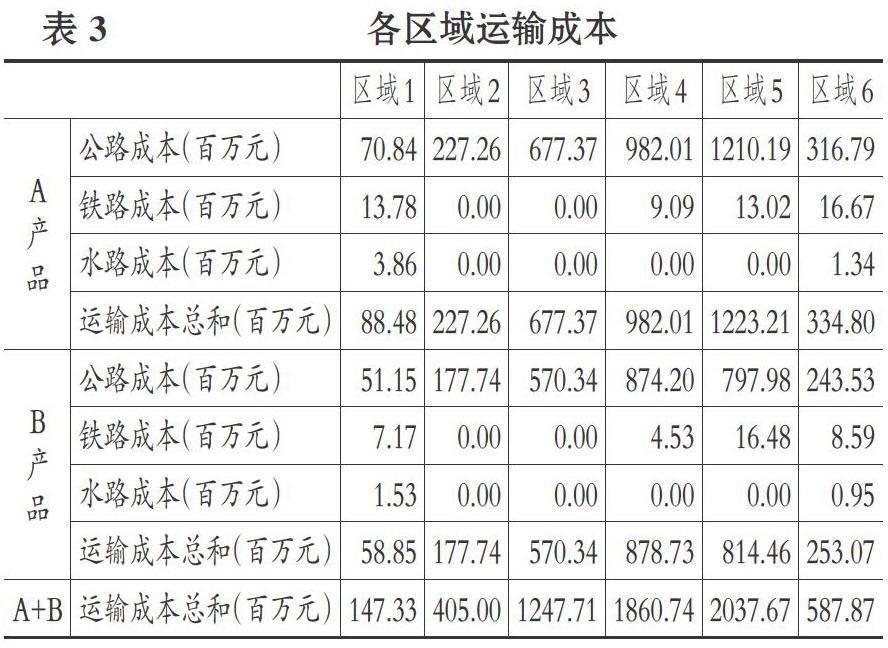
3. 密度经济判断模型。 在产品运输过程中存在多式联运， 各区域内物流基地与物流中转站的建立使物流企业内部出现了不同的运输分担机制， 形成了交通运输经济中的密度经济体系， 根据样本企业业务区域内的相关运输、成本数据， 计算业务区域内公路、铁路、水路运输成本C1、C2、C3; 样本企业以VOT为载运工具时平均时速V1， 运输货物时平均时速V2， 企业公路、铁路、水路运输平均里程L1、L2、L3， 企业公路、铁路、水路运输业务量Q1、Q2、Q3， 公路、铁路及水路运输业务单价P1、P2、P3， 公路、铁路、水路平均运输时间T1、T2、T3。 综合计算各区域内三种运输方式的成本， 结果如表3所示。

在密度经济模型中， 各业务区域内由多式联运形成的物流基地与物流中转站的节点网络， 承担了物流企業业务区域内运输成本的绝大部分， 因此， 在寻找降本空间时， 首先利用样本企业的基础数据挖掘出各业务区域内的平均运输成本和可能成本， 计算所得的可能成本与实际成本分别代表密度经济判断模型中的C和C， 两者之比则为密度经济系数Kd。 当Kd>1时， 企业实际运输成本较计算成本高， 表明物流企业在产品运输过程中存在部分无效成本， 存在无效成本的业务区域可以通过强化成本核算和运输管理等措施实现降本; 当Kd<1时， 企业实际运输成本低于计算成本， 表明企业成本管控水平较高或已经通过成本改善降低了运输成本， 形成了密度经济效应。 样本企业6个业务区域的成本值及密度经济效果， 如表4所示。

由表4可见， 除区域5与区域6密度经济性较低外， 其他地区均已实现产品运输的密度经济性。 此现象与地区发展水平密切相关， 在区域5与区域6， 由于其发达的公路网络及频繁的交通运输活动， 公路网络长期处于近饱和状态， 运输车辆在该区域路网上行驶速度低、燃油消耗大， 加上该地区相对于其他地区而言， 社会经济发达、人均消费水平高， 造成了运输成本的增加， 其密度不经济性的具体量化反映便是在区域密度经济模型中密度经济系数Kd高于1。 对于样本企业的其他业务区域而言， 公路网密度、社会经济发展水平低于区域5、区域6， 其理论计算成本会高于运输过程中产生的实际成本， 该结论在一定程度上验证了M2模型指标的适用性。

4. 网络经济判断模型。 运输是物流的关键环节， 运输过程中存在巨大的降本空间， 但与路网相对固定的铁路运输与水路运输相比， 公路运输线网的多样性可以为企业提供差异化选择， 企业可以通过优化公路运输线网来达到降本目的。 要想构建网络经济模型， 需要优化物流运输网络结构， 使各物流网络上的运输量达到均衡。

样本物流企业既有线网中共有8个目的地和6个物流基地， 通过网络经济判定模型对其主要线网进行优化以实现网络均衡。 程序第一次迭代结果如表5所示。

由表5可知， 物流网络中初始运输量并未达到均衡， 企业物流运输成本不断增加， 经过物流网络平衡分析， 企业物流网络能够实现均衡， 满足了网络经济性要求， 但是由于第一次迭代所得的均衡运输量与初始运输量相差较大， 不符合企业物流网络的实际情况， 还需要进一步优化。 分析发现， 部分目的地公路路网欠发达， 经济发展基础相对薄弱， 网络节点、网络路径较少， 体现出较低的联通度， 因此， 本文尝试性地在现有物流网络中增设4个二级中转站， 形成了新的物流网络。 对新的物流网络进行第二次优化迭代， 其均衡结果如表6所示。

公路运输线网优化后， 均衡运输量较第一次迭代有所增加， 可初步认为网络的经济性得到了提高。 但是， 时间价值也是物流运输经济性的重要度量指标， 企业在增加运输量的同时也会尽可能寻求时间成本的降低， 单纯的均衡运输量增加不一定代表企業运输网络经济的最优， 因此， 本文进一步计算了第二次均衡运输量下的运输时间， 结果如表7所示。

经过优化， 各路线上物流运输时间都呈下降趋势， 表明企业物流运输的时间成本也在降低。 结合表6、表7， 不论是从运输量还是运输时间上来说都存在相应的优化空间， 反映了样本企业现有的物流运输网络结构、分布的不合理， 如果以此为切入点， 细化、新增运输网络节点， 可以提高物流运输的网络经济性， 实现微观层面的降本增效。

在网络经济判断模型下， 两次迭代后均衡运输量的增加及运输时间的缩短也验证了M3理论的可行性。

四、结论

在规模经济模型下， 企业运营数据所反映出的多产品及特定产品的规模经济性能够为企业选择合理的降本方向、制定符合实际的降本方案提供参考， 企业可选择是通过控制各产品的生产规模还是通过提升劳动力水平、管理效率进行降本， 同时也能为企业决策是否开展多产品经营、是否对产品进行差异化定位、是否将特定产品作为新的业务增长点提供数据支持。 由于模型使用数据的拟合解析式可以反映规模经济最优区间， 但不能直接确认规模经济指标， 因此通过数据在一定程度上可以验证M1规模经济模型指标的适用性。

密度经济模型通过对各业务区域内铁路、公路、水路运输的实际成本与计算成本进行比较， 发现区域运输密度经济指标Kd与实际运输成本相吻合， 区域内多式联运机制、社会发展基础与密度经济性息息相关， 证明了密度经济指标Kd对物流企业的区域运输成本控制具有指导意义， 通过数据验证了M2密度经济模型指标的适用性。

在网络经济模型中， 使用交通运输网络平衡理论与网络经济理论对样本企业现有的物流网络进行分析。 通过增设物流运输网络节点、优化网络结构的方式， 提高了物流运输量、降低了物流运输的时间成本， 更好地实现了网络经济性， 为物流企业细化研究交通运输模式、合理规划运输方案提供了指导， 两次迭代后的均衡运输量和运输时间验证了M3网络经济模型指标的适用性。