二维混合矢量磁滞模型数值模拟的改进方法
李丹丹,乔振阳,朱聪聪,吴宇翔,李永建
(1.郑州轻工业大学建筑环境工程学院,郑州 450001;2.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130)
电工磁性材料广泛应用于电机、变压器等电气设备,对磁性材料的磁特性进行精确模拟,进而可以对电气设备的内部结构进行优化,从而提升设备的运行效率[1]。
1935年,Preisach提出了Preisach模型[2],使用Preisach磁滞算子和Preisach分布函数来模拟磁滞特性;文献[3]通过对Preisach磁滞模型的离散化,建立了超磁致伸缩驱动器的Preisach磁滞数学模型;1948年,Stoner等[4]提出了Stoner-Wohlfarth(S-W)模型,认为粒子磁化过程的平衡状态应满足能量最小原理。此外,常见的磁滞模型还有Jiles-Atherton(J-A)模型、Enokizono-Soda(E-S)模型、Play模型和Energetic模型等[5-8]。1992年,Friedman等[9]将S-W模型和Mayergoyz的矢量Preisach模型进行了扩展,提出了混合磁滞模型的思想。近年来,混合磁滞模型得到了学者们的广泛关注。Michelakis等[10]结合经典Preisach模型和S-W模型提出了一种适用于单畴单轴粒子的混合矢量磁滞模型,后来又将该模型扩展到了三维情况下[11];Chang等[12]以S-W模型为基础,采用Preisach分布函数计算矫顽力和相互影响场;Cardelli等[13]和Torre等[14]提出了Preisach-Stoner-Wohlfarth(PSW)模型,使用网络场来确定磁化强度的方向和大小。随后Cardelli等[15-16]又提出了DPC(Della Torre,Pinzaglia and Caredelli)模型,并使用DPC模型分析单个单畴粒子的磁化特性。文献[17-18]提出了一种新的矢量磁滞算子定义方法,建立了基于软磁复合材料的二维混合矢量磁滞模型;文献[19]提出了基于J-A/S-W模型的混合矢量磁滞模型,以S-W模型得出的三维各向异性的向量作为 J-A 模型的输入。对磁滞模型的研究有利于了解材料磁滞特性,为先进电工磁性材料的设计和优化提供帮助。此外,磁滞损耗模型是计算磁损耗的常用方法之一[20],对磁滞损耗模型的研究也有利于为研究磁损耗提供新方法。
二维混合矢量磁滞模型已经能够得到交变场和旋转场下的磁滞特性,但是所得到的曲线并不能完全闭合,模拟精度也有待提高。为此,从各向同性磁滞算子的单位磁化强度计算出发,结合S-W模型星形判定法则得出了改进后的二维混合矢量磁滞模型的表达式。给出了二维混合矢量磁滞模型的模拟步骤。并分别在交变激磁和旋转激磁条件下对软磁复合材料的模拟结果和实验测量结果进行了对比。
1 二维混合矢量磁滞模型
二维混合矢量磁滞模型是基于二维矢量磁滞算子建立的。根据S-W模型的最小能量原理将磁滞算子定义为由粒子磁化场产生的等势线包围的封闭区域。根据S-W星形判定法则[21],若外加磁场在算子外部,磁化方向为外加磁场所在的磁力线方向;若外加磁场在算子内部,则磁化方向固定为其进入算子时的方向,直至外场穿出磁滞算子时发生巴克豪森跃变,磁化方向转至穿出点处的磁力线方向上。外加磁场进入算子时的点为Preisach模型的开场阈值,离开算子时的点为关场阈值,开关阈值与矫顽力场有关。
当考虑相互影响场的作用时,各向同性磁滞算子的等势线方程为
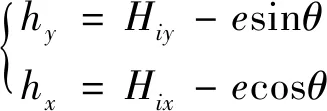
(1)
式(1)中:e为能量参数;θ为磁化强度M与x轴的夹角;Hix、Hiy为磁滞算子的中心点坐标。
模型使用许多磁滞算子来模拟磁性材料内部的磁畴,而磁滞算子的分布情况由Preisach分布函数表示。总磁化强度可以表示为
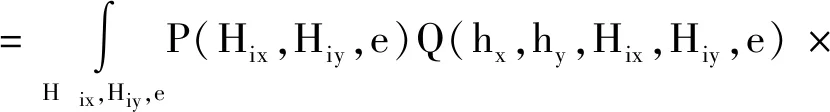
dHixdHiyde
(2)
式(2)中:P为分布函数;Q为单位磁化强度。
在二维混合矢量磁滞模型中,关键参数有:与矫顽力场有关的能量参数(e)、相互影响场(Hi)和算子数量(N)。
2 改进的数值模拟方法
由分析可知,二维混合矢量磁滞模型中的能量参数e控制磁滞算子的大小,各向异性磁滞算子为圆形,故可用r=-e表示磁滞算子的半径。从单个磁滞算子磁化强度的计算开始,结合S-W星形判定法则,从而建立各向同性磁滞算子单位磁化强度的表达式,如式(3)和图1所示。进一步再考虑算子数量以及相互影响场的影响,逐步实现对磁特性的模拟。
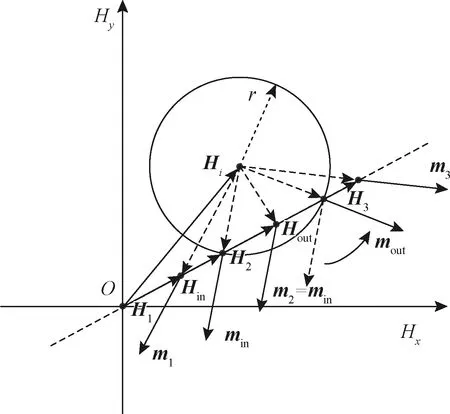
图1 二维各向同性磁滞算子单位磁化强度矢量的计算Fig.1 Calculation of the unit magnetization vector of a two-dimensional isotropic hysteresis operator
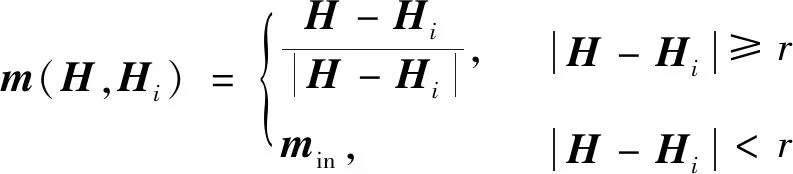
(3)
式(3)中:H为施加的外场;Hi为相互影响场,可以分解到二维坐标轴方向;min为磁场轨迹进入算子时的单位磁化强度。
在图1中,Hin为外加场穿入算子时的磁场强度,Hout为外加场穿出算子时的磁场强度。当外加场未穿入算子时,其单位磁化强度为m1,在进入算子后单位磁化强度保持进入时的磁化强度min不变,直至外场穿出算子时跃变为mout。
根据式(3)所示的单位磁化强度矢量计算方法,考虑相互影响场时单个磁滞算子和施加交变磁场时对应的磁滞回线如图2所示。其中Hix=0.2,Hiy=-0.2,θ=45°,r=-e=1,图2中虚线为外加磁场的磁化路径 (-1.5,1.5)—(1.5,-1.5)—(-1.5,1.5),实线为磁滞算子等势线。

图2 考虑相互影响场时单个磁滞算子和施加交变磁场时对应的磁滞回线Fig.2 A single isotropic hysteresis operator and the hysteresis loop when alternating magnetic field are applied with interaction field are considered
由图2可知,影响单个磁滞算子磁滞回线的参数有算子的大小r和相互影响场Hi。考虑多个算子的共同作用时,总的磁化强度计算式如式(4)所示,因此算子的数量N也是影响磁滞回线的参数之一。
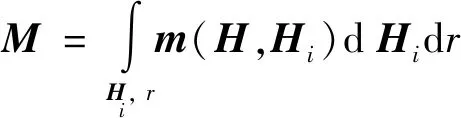
(4)
每个磁滞算子均具有单位磁化强度,在施加外场后,所有的磁滞算子都将受到外场的影响,因而宏观上所得到的磁化强度等于所有磁滞算子磁化强度的矢量和。
3 数值模拟步骤
二维混合矢量磁滞模型的模拟需要明确磁滞算子的分布规律,目前以高斯分布和洛伦兹分布较为常见[22-23]。提出了一种新的关于算子分布情况的确定方法,该方法认为磁滞算子的半径大小与其数量成反比,即磁滞算子越小其数量越多。该假设更加考虑了磁滞算子之间的相互作用,且更加接近磁性材料的物理本质,但从某种意义上讲也符合高斯分布函数。
改进的数值模拟过程采用网格点法,首先考虑一定磁场强度下会对磁化产生影响的区域,再对这个区域进行平面离散,得到的每个点即为磁滞算中心点的坐标;其次对于每个中心点,寻找其距离区域边缘的最短距离,将最短距离离散即可得到每个磁滞算子所考虑的半径的大小;再次,将施加的外磁场离散化,得到外场的磁化路径;最后对外场的每个点,计算所有考虑的磁滞算子对其的磁化影响,即可得模拟的曲线。具体数值模拟步骤如下。
(1)定义一个相互影响场平面,并将其离散为nxny个点,平面边界大小均为HB,每个磁滞算子的中心点坐标为(Hix,Hiy)。
(2)从磁滞算子中心点(Hix,Hiy)到平面边界HB的最短距离为R,计算公式为
R=min{|Hix-HB|,|Hix+HB|,|Hiy-HB|,
|Hiy+HB|}
(5)
(3)将式(5)中的R离散便可以得到所考虑的半径r,由此可得出半径r的磁滞算子数目nr。因此磁滞算子的个数可由式(6)计算得出。其中,对于每个中心点(Hix,Hiy),nr的取值依赖于r和HB的大小。因此对于施加不同大小的外场的情况下,算子的总数不是一个恒定值。
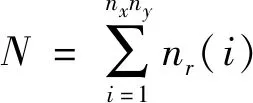
(6)
(4)对施加的外磁场进行离散,得到磁化路径Hx和Hy。在计算磁化强度时,外加场是作为输入量进行离散的。
(5)计算每个外场离散点(Hx,Hy)关于N个磁滞算子的磁化强度(mx,my),则最终M为
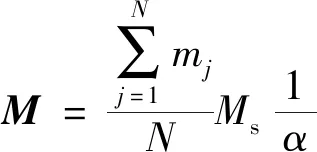
(7)
式(7)中:mj为离散点关于第j个算子的单位磁化强度;Ms为材料的饱和磁化强度;1/a为修正系数。
当外场最后一个离散点的磁化强度(Mend)不等于起始点的磁化强度(M1)时,将Mend设为M1并重复式(1)~式(5),直到Mend=M1,从而确保了模拟曲线的闭合。通过上述数值模拟步骤,将输入的外加磁场转化为输出的磁化强度后,即可得到模拟的磁化曲线,实现对磁滞特性的数值模拟。
4 实验验证
为了验证模型的有效性,将模拟结果与实验结果进行了对比。实验采用的软磁复合材料是SOMALOYTM500,其最大磁通密度为2.1 T (100 kA/m),剩磁0.25 T,矫顽力250 A/m,测量样品为22 mm3的立方体。实验采用的测量装置为河北工业大学的三维磁特性测量装置[24-25]。由于实验中测量的物理量为磁通密度矢量和磁场强度矢量,而模型中使用的物理量为磁化强度矢量(M)和磁场强度矢量(H),因此需要使用式(8)对物理量进行转化。根据SI标准,将磁通密度矢量B和磁化强度矢量M以T为单位表示,磁场强度矢量H以A/m为单位进行表示。
B=μ0(H+M)
(8)
式(8)中:μ0为真空磁导率,μ0=4π×10-7T·m/A。
4.1 交变磁化
在交变激磁场下对软磁复合材料的磁特性进行数值模拟,模拟结果与测量结果的对比如图3所示,nx=ny=10,最短距离(R)的步长为0.01。由于测量结果在x和y两个方向呈现出近似的磁特性,因此仅以y方向为例进行验证。
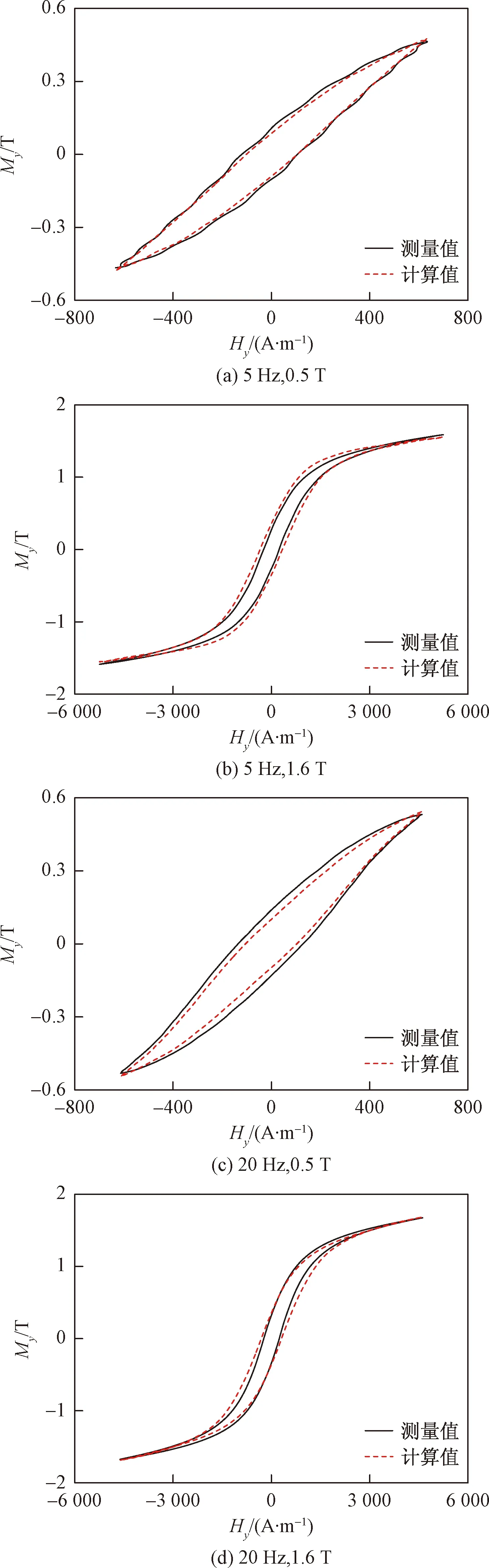
图3 交变激磁条件下模拟结果与测量结果的对比Fig.3 Comparison of simulated results and measured ones under alternating excitation field
分析表明,改进方法在低磁通密度和低频率交变磁场下计算的磁滞回线与实验结果吻合较好。但通过对比图3(a)和图3(b),发现改进方法的模拟精度随着实验控制的磁通密度的增加而降低。同时,通过对比图3(a)和图3(c),发现改进方法的模拟精度随着频率的增加而降低。在高磁通密度和高频率的激磁条件下,模拟效果有所下降,模拟结果容易出现误差,原因是随着磁通密度的增加,材料内部被磁化的颗粒情况过于复杂,需要进一步对算子的分布规律进行研究。
此外,由于施加的激励是两个方向同时施加的,但是在建模时将两个方向独立开来进行计算的,忽略了一个方向的激励对另一个方向磁化的影响,这也是模拟效果出现误差的原因之一。但是由于二维模型的磁特性描述目前仍存在不足,导致建模相对困难,因此关于二维动态磁滞模型仍需要进一步研究。
4.2 旋转磁化
同样地,在圆形旋转磁场下对软磁复合材料的磁特性进行数值模拟,旋转激磁条件下的磁特性通常用二维磁化强度Mx、My描述。在此,首先控制外加磁场为输入量将模拟的磁化强度与测量结果对比,再控制磁化强度为输入量将模拟的磁场强度与测量结果对比。所得的模拟结果与实验结果的对比如图4所示,旋转场的频率为5 Hz,nx=ny=10,最短距离(R)的步长为0.01。
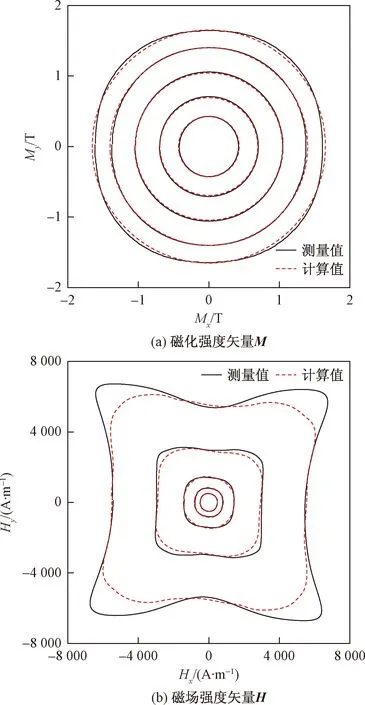
图4 旋转激磁条件下模拟结果与测量结果的对比Fig.4 Comparison of simulated results and measured ones under rotational excitation field
为了更加精确地模拟软磁复合材料的磁特性,采用最小二乘法将每组曲线模拟结果的修正系数进行了拟合,拟合公式为关于磁通密度峰值Bmax的多项式,从而可以动态地精确模拟任意激磁频率条件下软磁复合材料的旋转磁特性。
对比结果表明,改进方法在低磁通密度和低频率旋转励磁场下的模拟效果与实验结果吻合较好。其中图4(b)为改进方法的逆运算,利用磁化强度计算外加磁场。通过对比图4(a)和图4(b)可以看出,利用外加磁场计算磁化强度时,改进方法的仿真精度较高;而当采用磁化强度计算外加磁场时,模拟效果随外加磁场的增大而减小。原因是随着磁化强度或磁场强度的增加,模型参数逐渐不能确切反映材料内部磁畴的真实分布状态,需要对模型参数进行调整。
5 结论
通过对二维混合矢量磁滞模型数值模拟的改进,得到以下结论。
(1)从各向同性磁滞算子的单位磁化强度计算出发,得出了改进后的二维混合矢量磁滞模型的数值模拟方法。
(2)给出了二维混合矢量磁滞模型的数值模拟步骤,理论上给出的模拟步骤也可扩展到各向异性情况。
(3)数值模拟结果表明,改进后的数值模拟方法可以得到闭合的磁特性曲线,且模拟精度也有所提高。
(4)通过实验验证可以得知,提出的改进的数值模拟方法在低磁通密度和低频率下的模拟效果较好。

