计算机辅助公共服务设施的可达性分析

王 涵

(西安建筑科技大学 信息与控制工程学院，陕西 西安 710055)

0 引言

公共服务设施是居民基本生活的保障，其空间布局关系居民获取资源的便利程度。可达性能够识别出设施的匮乏区域，是衡量设施空间布局的有效途径。GIS技术的出现使得空间分析和可达性计算成为可能，但现有Arc GIS软件没有集成可达性算法，且研究多采用调查数据，数据样本量少且精度差。可达性的计算方法有很多，两步移动搜索法(Two-Step Floating Catchment Areamethod，2SFCA)得益于两步移动搜索的思想，在一定搜索域内分别搜索需求点和设施点，考虑了供需双方的供需规模及其距离因素对可达性的影响，能够很好地度量可达性，但2SFCA没有考虑设施在空间上的距离衰减效应与竞争效应。针对上述问题，文章考虑设施间的距离衰减效应与竞争效应，对2SFCA进行扩展，使用从电子地图上获取的兴趣点(Point of Interest，POI)数据，对Arc GIS进行二次开发，计算设施的可达性。

1 扩展的两步移动搜寻法

空间相互作用中，相互作用的强度随距离的增加而减弱，这种现象为距离衰减效应[1]，其本质是在2SFCA算法的搜索半径内增加一个距离衰减函数，考虑到居民出行意愿随距离的增加而降低，且距离越大，出行意愿降低的趋势越大，文章选择高斯函数作为距离衰减函数，如式(1)所示。

(1)

针对公共设施的竞争效应，已有2SFCA扩展形式包括Wan等[2]提出的三步移动搜寻法(Three-step Float-ing Catchment Area，3SFCA)、Luo[3]提出的胡弗型2SFCA(Huff 2SFCA，H2SFCA)。3SFCA提出当多个设施点给需求点提供服务时，设施点间存在竞争关系，为此引入选择权重，如式(2)所示，在计算可达性之前先计算需求点对设施点的选择概率，用以衡量设施点间的竞争效应；H2SFCA提出人们选择设施的行为会受到设施规模与出行成本的影响，因此，引入经典Huff模型对3SFCA的选择权重进行修正，如式(3)所示。综上，文章参考3SFCA与H2SFCA，考虑设施规模和居民出行成本，以高斯函数作为权重分配函数，计算选择权重，如式(4)所示，其中，Wij表示需求点i对设施点j的选择权重；Tij，Tik表示需求点i选择设施点j，k的权重；sj，sk表示设施点j，k的规模；dij，dik表示需求点i与设施点j，k的距离；g(dij)表示高斯函数。

(2)

(3)

(4)

综上，扩展的2SFCA算法的具体实现为：对每个需求点，以该点为中心，出行极限距离为半径得到搜索域，对落在搜索域内的设施点的服务规模，根据距离衰减函数赋予权重并求和，得到每个需求点搜索域内的总服务规模，计算需求点搜索域内某一设施点的服务规模与距离衰减函数的积与总服务规模的比值，即为需求点在其搜索域内对该设施点的选择权重，如式(4)所示；对每个设施点，以该点为中心、出行极限距离为半径得到搜索域，对落在搜索域内需求点的需求规模，根据距离衰减函数赋予权重并求和，得到设施点搜索域内的总需求规模，设施点的服务规模与总需求规模的比值即为每个设施点的供需比，如式(5)所示；对每个需求点，以该点为中心，出行极限距离为半径得到搜索域，对落在搜索域内设施点的供需比，根据距离衰减函数赋予权重并求和，结果即为每个需求点的可达性，如式(6)所示。

(5)

(6)

2 实验与分析

为验证方法的有效性，以Arc GIS10.1和Visual Studio 2010为平台实现扩展的2SFCA算法。以西安市碑林区小学教育资源为研究对象，居民点为研究尺度，计算居民点限定范围内小学的可达性。截至2016年年末，西安市碑林区户籍总人口约65万人，全区共有小学44所，小学专任教师1 771人，小学在校生3.8万人，占碑林区总人口的5.8%。

2.1 数据收集

从高德地图爬取了西安市碑林区800个居民点与44所小学的POI数据，并将经纬度坐标转换为投影坐标。以居民点小学在校生数量表示居民点的需求规模，小学师资数量表示小学的服务规模，居民点和小学的空间分布如图1所示。

2.2 搜索域确定

由2SFCA算法的定义可知，确定合理的搜索域是2SFCA算法的关键。缓冲区分析法[4]是指以点、线、面等实体为基础，根据一定半径为宽度，建立这些实体的缓冲区多边形的方法，文章使用缓冲区分析法确定搜索域的范围。根据《中小学校设计规范》提及的“城镇完全小学的服务半径宜为500 m”建议要求，取出行距离为500 m作为搜索域的半径。

图1 西安市碑林区居民点与小学空间分布

2.3 实验结果分析

利用扩展的2SFCA算法计算居民点搜索域内小学的可达性，结果如表1所示。自然分裂法基于数据的内在联系，旨在最大化组间差距并最优化组内相似值，因此，使用自然分裂法对可达性结果分级并统计，结果如表2所示。

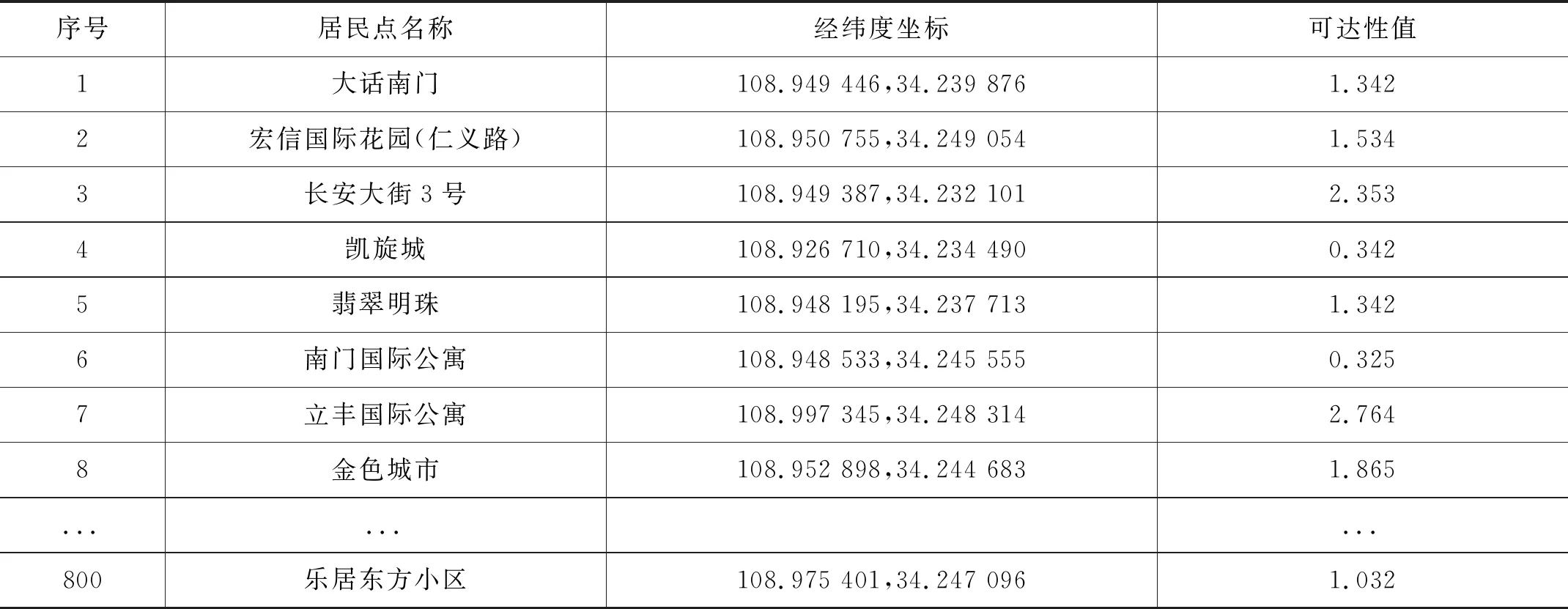
表1 西安市碑林区各居民点对小学的可达性

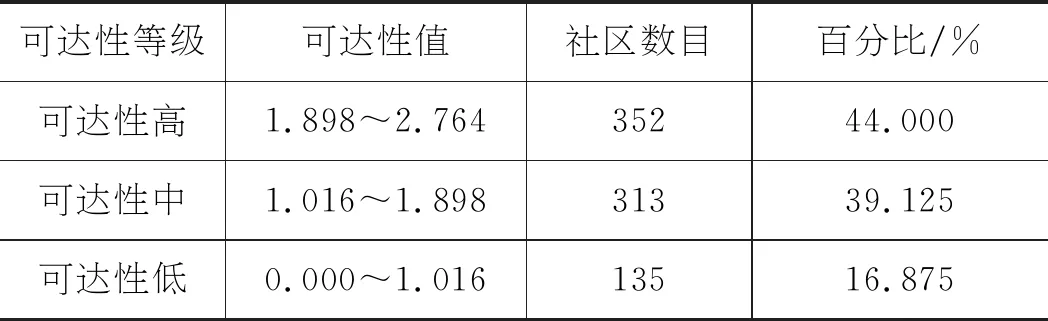
表2 可达性结果统计

可知，西安市碑林区小学的空间可达性较好，44%的居民点至限定范围内的小学可达性高，39.125%的居民点至限定范围内的小学可达性中，仅16.875%的居民点至限定范围内的小学可达性低。

3 结语

文章从供需双方出发，考虑设施的距离衰减效应与竞争效应扩展2SFCA算法，对Arc GIS二次开发实现算法与GIS软件的集成，使用电子地图数据，更为精准地计算公共服务设施的可达性，为城市规划提供自动化分析手段与量化参考依据。