环型圆管内对流动力学行为及数值分析
王贺元, 杨跃男, 柏孟卓
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
混沌是非线性系统特有的一种运动形式,产生于确定性系统的依赖于初始条件的往复稳态非周期运动,类似于随机振动而具有长期不可预测性[1]。1963年,气象学家洛伦兹在数值实验中发现混沌现象,随后,经过Kuhu、Li、和Yorke以及May等对混沌的进一步研究,到近代的吕金虎、陈关荣等又提出统一混沌系统[2]。这些开创性工作对混沌理论的应用起到了至关重要的推动作用。混沌理论在众多领域均有广泛的应用,如环型圆管内的对流问题:竖直放置的环型圆管内充满流体,环境温度下热上冷,当底部温度达到一定值时,管内流体发生对流现象。本文通过分析和仿真环型圆管装置所对应的数学模型的动力学行为,分析解释了圆管内的对流现象。
1 环型圆管对流的数学模型
竖直放置的环型圆管内充满流体,环境温度下热上冷。开始流体静止,上下流体内的温差到达一定值后,流体开始在管内对流耗散,忽略粘性流体运动时能耗所产生的热量,并假定通过管壁的热传导速率正比于流体温度与壁外环境温度的差,得出能量方程的近似分解式[3]。文献[3]给出了该数学模型的动力学方程式:
(1)

1.1 系统的对称性和不变性
该类洛伦兹系统具有对称性,即在变换(X,Y,Z)→(-X,-Y,Z)下具有不变性,系统(1)关于Z轴具有对称性,且这种对称性对所有的系统参数均成立[4]。
1.2 耗散性和吸引子的存在性
1.3 平衡点及稳定性

再线性化,就得到该平衡点的稳定性方程为
将(X0,Y0,Z0)=(0,0,0)带入稳定性方程,得该点的雅可比矩阵为
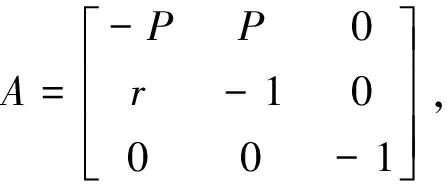

当0

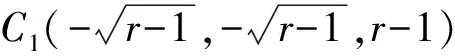
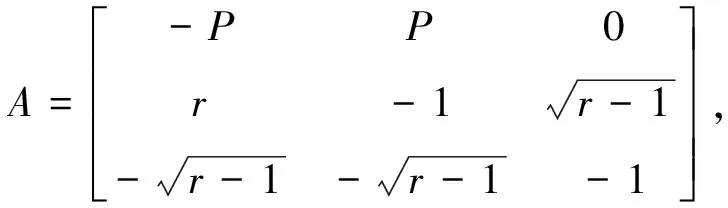
特征方程为λ3+(2+P)λ2+(r+P)λ+2P(r-1)=0。

2 系统参数的影响
根据上面的分析,随着系统参数的改变,系统平衡点的稳定性也发生变化,从而系统将处于不同的状态[9]。下面进行分岔及轨道的讨论与分析。
当r≤r1=1时,只有一个定点O(0,0,0),它是稳定的。当r>r1时,O变为不稳定,同时出现了另外2个稳定的定点C1和C2,故在r=r1=1时出现音叉分岔。当r
3 系统的分岔与混沌的数值模拟
随着雷诺数r的增大,类洛伦兹系统(1)的动力学行为发生了一系列变化,如出现霍普夫分岔和混沌等非线性现象[12]。首先,对系统(1)进行数值求解,进而画出仿真图以揭示系统的混沌行为。图1给出了状态变量x随r变化的全程分岔图,展示了系统分岔和混沌演变的全过程,系统通过阵发途径发生混沌,在混沌中出现了3个周期窗口,说明此系统的周期运动比较稳定[13]。图2给出了系统随参数r变化的最大Lyapunov指数谱。从图中可以看出最大Lyapunov指数大于零的区域与分岔图1显示的混沌区域是一致的[14]。
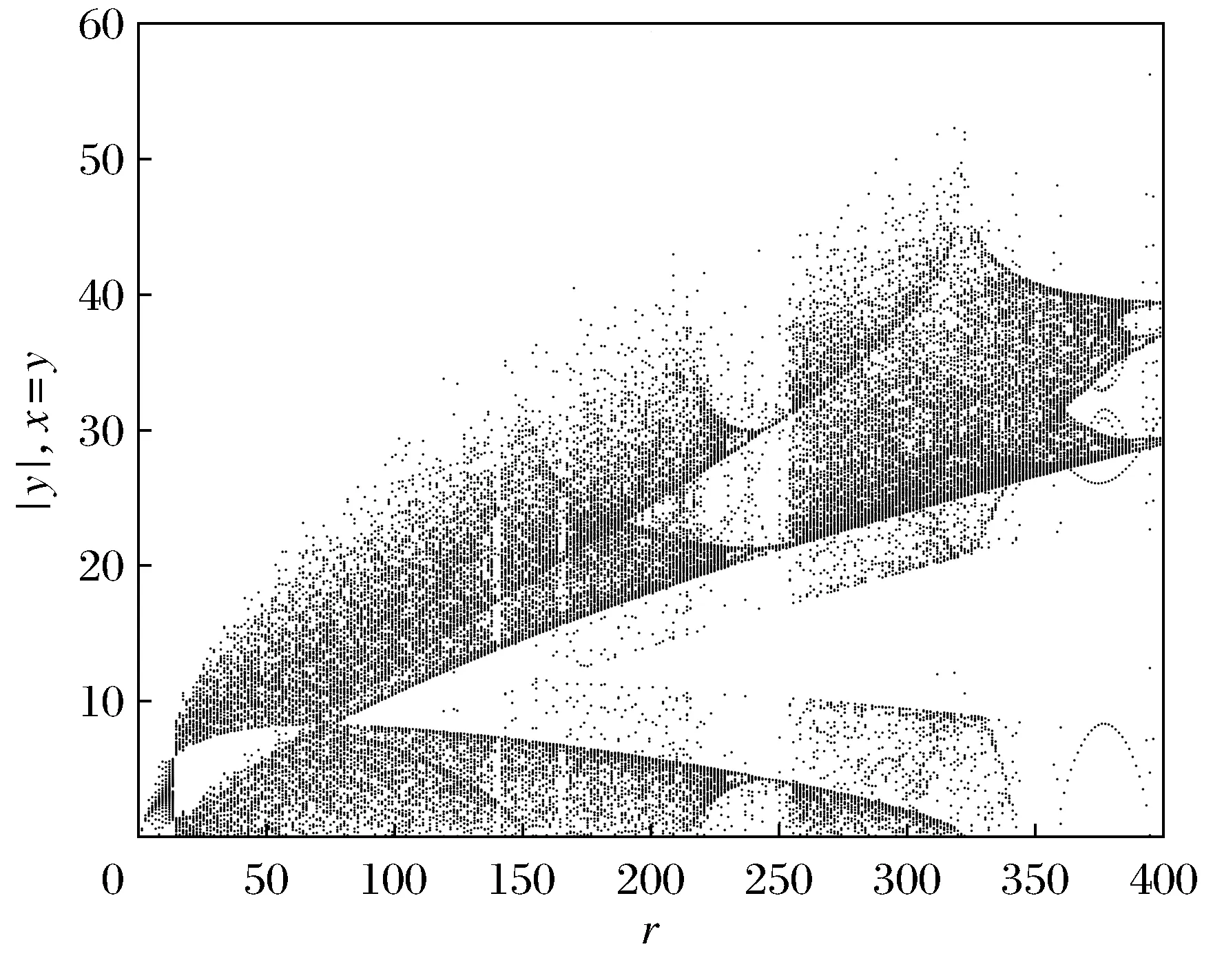
图1 系统(1)雷诺数在0≤r≤400范围内状态变量x的分岔图
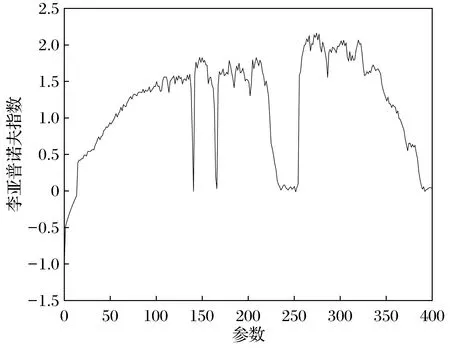
图2 系统(1)雷诺数在0≤r≤400范围内最大Lyapunov指数图
4 结 论
本文研究了环型圆管内的流体对流的三模态类洛伦兹型方程组的部分动力学行为。数值模拟了由不稳定周期到达混沌所展现的动力学行为。仿真结果表明,此系统随着参数增加,由不稳定的周期轨道经暂态混沌直接进入混沌状态。相对应的物理现象表现为随着底部温度的逐渐升高,管内流体发生复杂的对流现象。环型圆管的对流行为是由于雷诺数r的不断增大产生,在此过程中系统发生由稳定的不动点到周期轨道,再失去稳定性进入混沌区域[15]。
致谢感谢沈阳师范大学博士启动基金项目的支持(054-91900302009)。