The effect of forced oscillations on the kinetics of wave drift in an inhomogeneous plasma

V I EROFEEV

Institute of Automation & Electrometry of the Siberian Branch of the Russian Academy of Sciences, 1 Koptyug Prosp., 630090, Novosibirsk, Russia

Abstract

Keywords:informativeness of plasma kinetic scenario, the ensemble method, asymptotic convergence of perturbation theories,correlation analysis of plasma kinetics,kinetic equation of wave drift in phase space

1.Introduction

In essence, physics as a science is aimed at describing the changes that occur in specific physical systems under the influence of external factors.The corresponding changes cannot occur instantaneously: even with sudden changes in key external factors, the transition of a system from the initial state to the final state takes a certain period of time.Meanwhile,the final state is itself often determined by the subtleties of the system’s evolutionary scenario.In this regard, studies of physical systems’ evolutionary scenarios are of great importance.Motivated by this,we have previously advanced the concept of the informativeness of a physical theoretical scenario:the longer the scenario adequately depicts the real picture of the macrophysical evolution of a system, the higher the informativeness of the scenario[1-7].We formulated this concept in studies of various nonlinear plasma phenomena [5, 6, 8-12].Analyzing similar studies by other authors,we have shown that generally,such scenarios do not have appropriate informativeness.That is,they have an arbitrary correspondence to objective pictures of plasma evolution in the corresponding physical situations.We have explained that theorizing in plasma kinetics generally allows one to generate very different and even incompatible scenarios of plasma evolution from a given initial state and to develop these diverse scenarios in an equally rigorous manner.

We have clearly identified the key interrelated reasons for the uninformative theories: the lack of a proper understanding of the significance of the asymptotic nature of the convergence of successive approximations to a plasma scenario and the unwise practice of replacing real plasmas by probabilistic ensembles of plasmas.The most detailed explanation of these reasons can be found in[13]1The first references to the failures of traditional theoretical deductions due to the neglect of these reasons date back to 2002 [8, 14].Further arguments for the need to refrain from replacing real plasmas by plasma ensembles and the need to take into account the asymptotic convergence of successive approximations of the plasma kinetic scenario were presented in[3-6,10-12,15].Finally,a systematic discussion of the informativeness of plasma kinetic scenarios and methods for increasing it is given in monographs [1, 2]: they present our previous studies in aggregate..The first of these reasons allows one to develop different models of plasma kinetic evolution from a given initial state, even on the basis of a single nonlinear perturbation theory, by varying its leading-order approximation.(The point is that different lowest-order approximations of the same nonlinear perturbation theory yield different conditional limits of the theory that correspond to different models of plasma evolution.) As for the second reason for uninformative theories, it suffices to say that the conclusions about the mutual influence of the statistics of an ensemble of plasmas cannot but substantially depend on the ensemble’s composition and,therefore,cannot be regarded as objective laws of the physical evolution of a real plasma.

The knowledge of the above reasons allowed us to develop a technique for reducing a full plasma description to the most informative kinetic models of plasma evolution.This differs from previous approaches by rejecting traditional plasma ensemble averaging and in using direct time integration of the intermediate evolution equations that appear when reducing the full plasma description.In view of the purpose of our theoretical apparatus, it is most natural to refer to it as a highly informative correlation analysis of plasma kinetics.Currently, it focuses mainly on the problems of weakly turbulent plasmas,albeit its adaption to other plasma problems is extremely desirable.

The basic ideas of our approach to the kinetic modeling of plasma evolution are presented in a number of publications.The most systematic presentation can be found in monographs[1,2].Some further development of the theory is reported in [3, 13], which supplement the monographs by clarifying the state of the current understanding of the problem of theory informativeness.In those papers, we have adapted our technique to the development of highly informative kinetic scenarios for inhomogeneous plasmas with weakly turbulent fields of arbitrary waves (not only potential ones).In these plasmas, inhomogeneities in the spatial distribution of plasma particles induce wave drifts in normal space and in wavenumbers.A paper by Erofeev[3]contains a derivation of a scenario of the drift of electromagnetic waves in a cold ionized plasma with a small leading magnetic field,and[13]presents a derivation of a scenario of the drift of long Langmuir waves in a cold magnetized plasma.

It should be noted that wave drift is a linear plasma phenomenon.A somewhat informative scenario of such a phenomenon can be developed not only in our paradigm of modeling the kinetics of plasma physical evolution, but also on the basis of some traditional approaches to plasma kinetic research.Accordingly, it is necessary to analyze the correspondence of our results with those of our predecessors.Note that we have uncovered terms in the corresponding wave drift scenarios that were not known in the plasma literature,but an adequate explanation of their appearance was not given.The current paper is intended to fill this gap.We will show that these terms are related to the effect of non-natural oscillations of inhomogeneous plasma that are forced when waves travel through it:these forced oscillations modify the equation of the energy balance for plasma collective motions.

Presenting this study, we should explain the logic of the thought process in[3,13]:their findings form the basis of this study.However, in this paper, we are unable to describe the corresponding know-how to a full extent.We suppose that the reader can read paper [13] and learn the subtleties.Equally,all the questions regarding our notation can be resolved via familiarization with our previous papers.Nevertheless, here we outline the main ideas of our research.

This paper is organized as follows.In the next section,we shall explain to a greater extent the motivation of the study.Here, we outline the logic of the formulation of the traditional equation of wave drift in phase space(section 2.1).We then clarify the basic distinctive feature of our wave drift scenarios.In parallel, we analyze the difficulty of the previously suggested explanation of the appearance of the extra terms in our wave drift scenarios.The logic of the development of highly informative plasma-kinetic scenarios will be clarified in section 2.3.Section 3 contains additional comments on traditional scenarios of wave drift.The reason for the difference between our wave kinetics and the traditional one will be discussed in section 4.At the end of this section,we shall discuss the defectiveness of geometrical-optic models for the drift of non-potential plasma waves.Final comments will be given in the conclusions.

2.Additional comments on the motivation for the study

In developing kinetic scenarios of wave drift in phase space,we achieved acceptable informativeness by assuming that the spatial scale of plasma inhomogeneity is large compared to the typical wavelength in the wave spectrum.This is consistent with the central assumption of geometric optics underlying the traditional theorizing on wave propagation in inhomogeneous media.In view of this, we should especially emphasize that our reasoning in developing wave drift scenarios differs substantially from the typical reasoning for that theorizing.We recognize geometric optics as a method that is scientifically sound only for constructing images using rays.As for the other traditional field of application of geometric optics, an approximate description of wave fields in various media, we question the degree of validity of the corresponding approaches.Due to this, the intended comparison of the new and traditional scenarios of the kinetics of wave drift acquires a special significance.In making this comparison,we shall comment a bit more on problems with modeling plasma wave phenomena by means of geometric optics.

Let us give some historical excursus to traditional theorizing on wave drift.

2.1.The logic of the formulation of the traditional concept of plasma wave drift in space and wavenumbers

According to traditional views, the spatial transfer of wave energy is determined by the wave’s group velocity (see, e.g.,[16], p.77).When moving through the medium along the path of this transfer with the wave’s group velocity, concurrent changes are observed in the wave vector of the wave.The corresponding rate of change in the wave vector is the sign-inverted gradient of the wave’s natural frequency.On the basis of this knowledge, our predecessors proposed a kinetic equation for waves.Conceptually,it was derived to model the evolution of the distribution of some quasi-particles or,alternatively, single waves.It was assumed that a real wave field in a plasma, particularly in a turbulent one, can be divided into independent wave packets that are rather compact both in normal space and in the space of wave vectors.Each of them is characterized by a guiding natural frequency that is the weighted natural frequency of the harmonics of the packet.The guiding natural frequency plays the role of a Hamiltonian that governs the time transformations of the coordinates of the packet (the spatial position) and the conjugated momentum components (the leading wave vector of the packet).

Since different wave packets can differ significantly in their energies, theorists have suggested considering each packet as a set of identical quasi-particles.In accordance with tradition, the number of quasi-particles in a particular packet is related to the corresponding value of the wave action, i.e.,the ratio of the total wave energy in a packet to its guiding natural frequency.(Rather convincing, though indirect, support for this tradition is provided by considering plasma waves from a quantum viewpoint,see,e.g.,[17].)This has led to the introduction of the distribution of quasi-particles in the phase space of their spatial positions and wave vectors.Commenting on the traditions of the theory, we focus on characterizing their distribution by means of the wave number density, that is based on the Tsytovich formulae [18]:

Here, the superscript σ denotes the type of wave (Langmuir,ion sound, electromagnetic etc.),kandrare the wave vector and the spatial position, respectively,is the mean energy density in waves of a given type per unit of the ⊗K R phase space at the current point (k r,).(Hereinafter, the ⊗denotes the product of two spaces, and also the direct tensor product.)

According to the above ideas,the continuity equation for the energy densityin terms oftakes the form

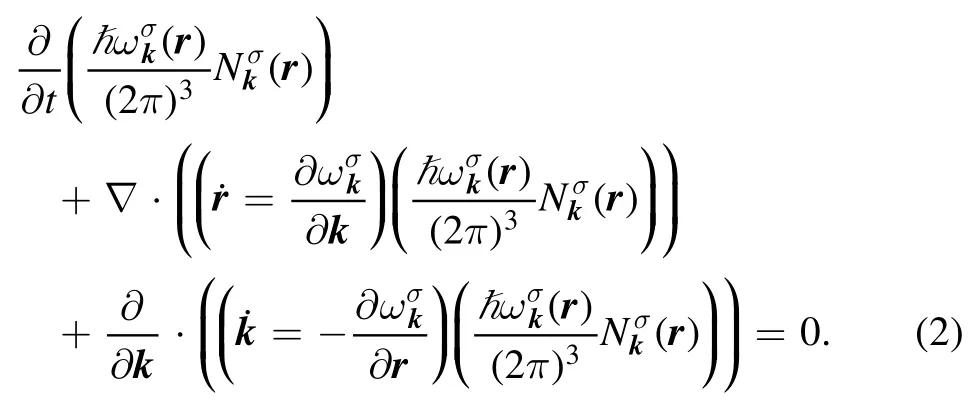
This is equivalent to the simpler equation known as the kinetic equation of wave drift,

We shall call(3)the wave drift equation.It is obtained under the assumption that the waves do not experience pumping or dissipation.

The above method of introducing the wave drift equation evokes a number of questions regarding its validity.In particular, the possibility of dividing the real wave field in an inhomogeneous plasma into wave packets with small widths in wave vectors and still acceptably small spatial dimensions seems doubtful.However,the idea of a kinetic equation of the above type was readily accepted by the plasma theoretical community.The earliest uses of wave drift equations of this kind were by Soviet researchers,see,e.g.,[17,19,20].Efforts to substantiate the concept of this equation were documented in [16, 21-28].Further attempts to extend the idea of the wave kinetic equation to more complicated plasma situations were undertaken in[29-31].Additional mentions and uses of the equation can also be found in [32-35].

Here, we have only cited a small portion of the publications that are somehow related to the problem of modeling the kinetics of transfer of waves in their phase space.And finally, we note that the introduction of the equation in research papers is usually motivated by semiheuristic ideas.

2.2.Subtleties of the physical situations considered in [3]and [13]

A common feature of the physical situations considered in studies [3, 13] is that waves possess both electric and magnetic fields.To put it in other words, a wave’s electric fields have, in addition to the potential components, some solenoidal ones.The second of these studies has permitted us to significantly vary the portion of the solenoidal component in the wave: it depends strongly on the wave vector.As a result, we have found that the larger this component, the larger the deviation of the wave’s kinetics from the wave drift scenario proposed by different researchers in previous studies.It was assumed that this fact provides evidence that the traditional theory does not contain a concept of wave energy density that fits an inhomogeneous plasma[13].However,the difference between our and traditional pictures of wave drift cannot be eliminated by modification of the usual wave energy density.The point is that the corresponding modification could be made only by adding a correction of the order of the wave energy density multiplied by the plasma inhomogeneity parameter.That is, its ratio to the usual wave energy density should have been of the order of the ratio of the wavelength to the characteristic length of the plasma spatial inhomogeneity.Accounting for such terms in the continuity equation for the transport of wave energy would lead to the appearance of terms in the equation that are of the second order in the plasma inhomogeneity parameter.Their consideration is beyond the accuracy of our wave drift equations, whereas the observed difference involves terms of the first order in this parameter.

The foregoing completes the motivation of the present study: to identify a more realistic reason for the discrepancy between our wave drift scenarios and their traditional counterparts.We shall show that it is related to the effect of nonnatural oscillations of inhomogeneous plasma that are forced in the plasma by the waves traveling through it.We shall call them forced oscillations.They accompany real waves in their travel, receiving from them the energy of the plasma’s collective motions and returning it back (depending on the situation).

In the next section, we will outline the milestones of our derivation of the wave drift equations.Section 3 contains additional comments on traditional wave drift scenarios.The reason for the difference between our wave kinetics and traditional ones will be discussed in section 4.Final comments will be made in the conclusions.

2.3.The logic in developing informative plasma kinetic scenarios

The starting position is a full plasma description,i.e.,a plasma description using simultaneous Maxwell[36]and Klimontovich[37,38]-Dupree[39]equations.The latter equations govern the evolution of Klimontovich’s distribution function [37, 38]that we will call a microdistribution.Averaging it over a reasonably wide neighborhood of the current point (r,p) of the R ⊗P phase space,we construct a distribution functionfα(r,p,t)of the Vlasov type [40]2In a slab plasma geometry, which we assume, one can use as the above neighborhood a six-dimensional parallelepiped with elongated spatial dimensions in level planes of plasma density with its center at the current point(r , p).For simplicity,the parallelepipeds can be assumed to be uniform at each point of the phase space..Its key distinction from Klimontovich’s distribution is that it does not contain information about the spatial positions and momentums of individual charged plasma particles.The evolution equation for the function fαis derived from the Klimontovich-Dupree equation by calculating the balance of particles that enter the averaging volume and those that leave it (per unit time).The corresponding rate of change of fαdepends on the average product of the microstructural part of the microdistribution,δNα(r,p,t)=Nα(r,p,t)−fα(r,p,t),and of the corresponding microstructural partδF(r,t)of the electromagnetic feild tensor (EMF tensor)F(r,t).In view of this, we introduce a two-point correlation function,〈δNα(r,p,t)δF(r′,t′)〉, in which we have intentionally split the time and spatial variables of two objects under the averaging sign to simplify the calculation procedure.Using the Klimontovich-Dupree equation, one can derive an evolution equation for the two-point correlation function.This function is advanced in time by the three-point correlation functionδ〈Nα(r,p,t)δF(r′,t′)⊗δF(r″,t″) 〉.In turn, the three-point correlation function is advanced in time by the four-point correlation function〈δNα(r,p,t)δF(r′,t′)⊗δF(r″,t″)⊗δF(r′′′,t′′′)〉,etc.

The concepts of the multipoint correlation functions introduced above imply an averaging over the phase space that is based on the following principles.Therandparguments of δNαrun through the neighborhood in the phase space that was chosen to construct fαat the current point(r,p).The spatial arguments of all the other objects under the averaging sign vary synchronously with the spatial argument of δNα; the differences between these arguments are fixed in the averaging.

The set of evolution equations for the multipoint correlation functions is infinite.It cannot be integrated in full.However, it can sometimes be truncated at some finite order,and on the basis of the retained equations, the researcher can develop a somewhat informative plasma kinetic scenario.In particular, this can be done in the case of a weakly turbulent plasma.Then the truncated hierarchy of the evolution equations can be reduced to a pair of simultaneous evolution equations.The frist is the above evolution equation of the distribution function fα,and as the second of the equations,the researcher may choose the evolution equation of the two-time correlation function(Here, the averaging is performed over the spatial projections of the six-dimensional neighborhood used to calculate the distribution fαat the current point in phase space (r,p), with the difference between the spatial variables of the two objects during the averaging being fxied again.) The derivation of these two simultaneous equations completes the first step of developing the plasma kinetic model: the development of a two-time formalism.We have previously considered such derivations in great detail and shall not present them here.(The reader can find them in [1, 2, 41, 42].) We only discuss its similarity to the hierarchy of equations after Bogolyubov[43]-Born-Green [44] Kirkwood [45, 46]-Yvon [47] (the BBGKY hierarchy).The above-mentioned hierarchy of the evolution equations of multipoint correlation functions, preceding the equations of the two-time formalism, resembles the BBGKY hierarchy only by the fact that both of them consist of a myriad of equations.The ideas underlying these hierarchies are substantially different.Having understood the necessity to refrain from the traditional substitution of real plasma by an ensemble of plasmas,we have been forced to replace it by an averaging in the phase space of plasma particles.The implementation of this averaging strongly depends on the geometrical and other physical aspects of the situation under study and therefore cannot lead to any universal plasma kinetics.The hierarchy of BBGKY equations was believed to be a universal system of plasma kinetics.However,it is devoid of any sense outside the paradigm of plasma ensemble studies.In particular, when refraining from substituting a plasma ensemble for real plasma,Bogolyubov’s method of sequential integration of the original‘full’ N-particle distribution function over the coordinates and momentums of individual charged particles gives no more than Klimontovich’s distribution functionNα(r,p,t)(if the indistinguishability of particles of a given type is supposed).That is,the corresponding procedure leads no further than to the starting position in the problem of reducing the full plasma description to a simpler plasma kinetic scenario.

In the second stage of developing the plasma kinetic scenario, the two-time formalism is reduced to a description of plasma evolution in terms of functions depending on a single time variable.For the problem of wave drift, this reduction involves developing a scalar function, the wave spectral density,which is the core of the two-time correlation function in some sense, and in terms of which, the very twotime correlation function can be expressed with arbitrarily high precision accessible for a particular situation.The requirement that the resulting two-time correlation function Φ (r,t,r′ ,t′)should satisfy the Maxwell equations both att＞t′and att＜t′defines the dependence of the wave spectral density on time.

The main steps in reducing the two-time formalism to the kinetics of wave drift are as follows.

Due to the plasma inhomogeneity, different spatial harmonics of the two-time correlation function influence each other.To analyze this influence,it is convenient to define the spatial Fourier transform of Φ(r,t,r′,t′)as

This Fourier transform is self-adjoint:

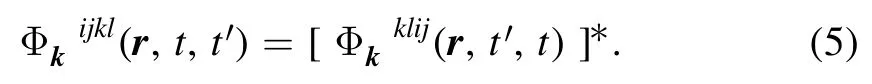
The evolution of Φk(r,t,t′)is governed by proper approximations of the Maxwell equations.For studies of linear wave phenomena, the latter take the form

In writing these formulae, we used the notation of tensor analysis.For an unambiguous interpretation of the formulae,co- and contravariant tensor indices are distinguished.Latin letters are used for all components of 4-vectors and 4-tensors,with their time-like components being indexed by 0.Greek letters are used to denote the spatial components of 4-vectors(-tensors), with the only exclusion being α: we use it to denote the type of charged particles.The nonzero components of the metric tensor are−g00=g11=g22=g33=1.The Einstein summation convention is implied:

The tensorσk(r,t,t′)has the meaning of the Fourier transform of the conductivity tensor.Its linear approximation is expressed in terms of the function Rαk(r,p,t,t′)that characterizes the linear response of the two-point correlation function to the variation of the two-time correlation function.The corresponding expression is

In turn, the function Rαk(r,p,t,t′)is expressed in terms of the bare Green function0Gα(r,p,t,r′,p′,t′):

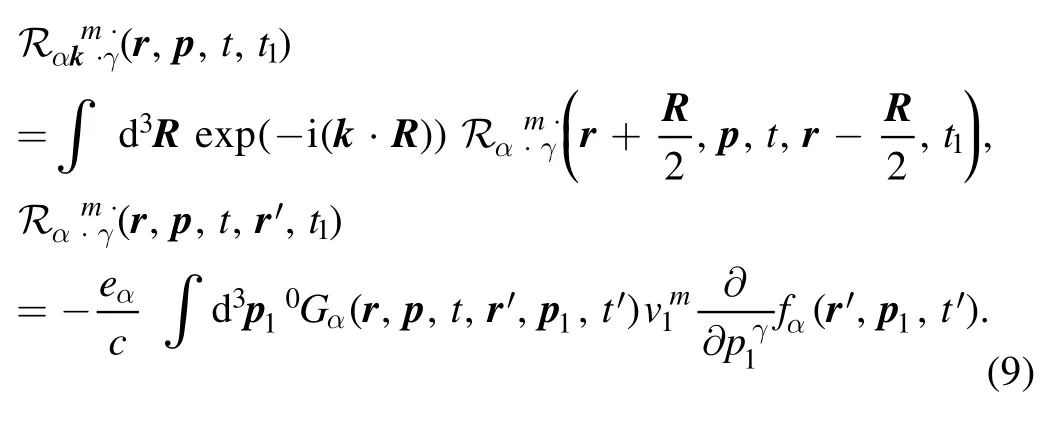
The bare Green function is a solution to the equation

that satisfies the causality principle.That is,att＜t′.The tensor0F(r)describes the external stationary magnetic field (if any).The symbol vmdenotes the particle relativistic 4-vector divided by its relativistic factor.(That is,vβare the physical components of the usual particle velocity,andv≡c0.)

At this point, it seems appropriate to comment on the relationship between the concept of the equations we proposed and the theoretical basis for modeling wave kinetic processes that is being developed by McDonald and his colleagues [22-24].The latter starts with the introduction of some pair functions and a definition of the relations that they satisfy.Like us, they split the spatial and temporal variables of objects that they multiply to organize these pair functions.The corresponding functions and relations are then subjected to the Weyl transformation (see [48], page 274) to get a more convenient basis for further theoretical considerations.In that basis,the analog of our two-time correlation function Φk(r,t,t′)is the Weyl symbol of the tensorE⊗Ewhich depends on a somewhat different set of variables:r,t,kandω.(HereEstands for the electric field, and the superscript denotes the Hermitian conjugate of the object.)Then,using the equations for the given Weyl symbol, McDonald and his colleagues put forward ideas regarding the symbol structure and its rate of temporal change.

We regard it as a large advantage of McDonald’s considerations that he develops from the very outset the theory of relations of pair functions.This allows him and his colleagues to evade the dilemma of whether the phases of waves present in the plasma are random or not:the notion of the wave phase becomes foreign to the theory.Note that we have also found some aspects of Weyl symbol calculus useful: our transformation of the approximate Maxwell equations to their Fourier representation (6), (7) is factually a calculus based on a truncated Weyl transformation.

As a disadvantage of McDonald’s ideas,we would like to mention the absence of an explicit recipe for forming reliable statistics.Up to the moment of advancing the idea of the structure ofE⊗E(r,t,k,ω), he does not discuss any specific averaging aimed at reaching the statistical reliability of the theory’s objects.This idea itself implies some unspecified averaging.However, the corresponding indirect averaging is certainly not aimed at increasing the informativeness of the corresponding theoretical scenarios.

An obvious sign of ignoring the problem of theory informativeness in McDonald’s method is as follows.The full-scale Weyl transformation itself assumes the neverceasing existence of the evolving plasma,since it manipulates the temporal Fourier transform of the history of plasma evolution.Meanwhile, ionized plasma can be produced by some method and eventually dies out, say, due to particle recombination.The Weyl transformation then involves supplementing real plasma history by speculative assumptions about non-existent plasma states in the distant future.The latter cannot but reduce the informativeness of the corresponding plasma theoretical scenario.

Let us return to the main narrative.In the problems discussed here,the main contributors to the two-time correlation function are natural oscillations.Their image can be developed on the basis of equations (6) and (7), with the omission of the terms containing spatial derivatives.

Natural oscillations are functions that decay rather slowly with increasing delay of their entry time argument from their exit time argument.The other case is for the conductivity tensor.Below,we introduce a transformation of its dependence on the difference between its entry and exit time variables to the frequency dependence.Evidently,the characteristic rate of decay of the original is of the order of the characteristic width of the corresponding Laplace transform in frequencies in the vicinity of the natural frequency of the natural oscillation.In a cold plasma,the latter is of the order of the oscillation’s natural frequency itself, which is large compared to the rate of decay of the oscillation.Due to this, equation (7) can be additionally simplified in the time domaint−t′≫( Δω)−1;see the derivation of equations(3.15,3.16)in[13].(Here Δω is the characteristic width of the turbulence spectrum in natural frequencies.) This permits us to form the following approximation of the two-time correlation function:

Here, the superscript σ is introduced to characterize the polarization of the oscillation, i.e., the type of wave: Langmuir, fast or slow electromagnetic, ion sound, etc.The superscript s=±is used to differentiate between the parts of the transformΦkthat correspond to waves propagating in opposite directions.The functionis the complex natural frequency of the oscillation.The tensoris the wave polarization tensor.

When writing the right-hand side of equation (11), we took into account property (5).Due to this,the functionis real-valued and nonnegative [12].It is this function that we call the wave spectral density and use to describe all the effects of plasma natural oscillations.

We normalize the polarization tensor by unity:

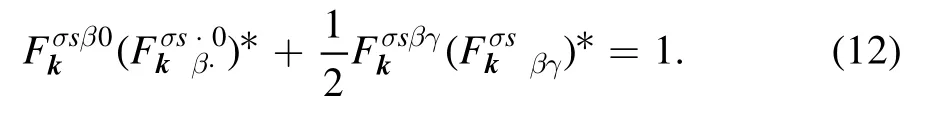
Note that Maxwell’s equations rigidly prescribe the dependence on time only for the structurein its unity.Thus, there some arbitrariness remains in the distribution of this time dependence between the polarization tensor and the exponential factor: the natural frequency is determined up to the time derivative of the phase ofIn our linear problems of wave drifts in stationary plasmas, we can assume that the polarization tensor does not depend on time at all.

We now address the terms of equations (6) and (7) that contain spatial derivatives of the two-time correlation function and its derivatives in wave vectors.To account for them,we should add a correctionto the approximationWith the formal substitution of the corrected approximation into the equations,we recognize that the above terms of the equation produce a motive force that advances the correctionin time.Within the accuracy of our consideration,we can integrate this force from = ′t tto larger values of t, neglecting any deviation of the approximationfrom the structureProvided that the initial value ofis properly selected, we can express the additionfor all ＞ ′t tin terms of the key features of natural oscillations.Within our two-time formalism, it is natural to refer to this addition as a forced oscillation.

It should be stressed that the initial value ofcannot be nullified for the vector wave field in an inhomogeneous plasma.The considerations in [3, 13] were performed without prior understanding of this fact, and yet they have indirectly indicated that this should take place.Compared to the case of a potential wave field,the case of a vector wave field implies a larger number of restrictions on the EMF,due to the need to satisfy Maxwell’s equations.The latter equations contain the derivatives of natural oscillations with respect to the wave vectorkand the spatial coordinatesr,which derivatives cannot be expanded in the natural oscillations.One of the reasons for the latter is that the dependence onrappears in the relation between the magnetic field components of the wave with certainkand the components of its electric field.

We note that the impossibility to nullify the dataspoils the traditional interpretation of wave energy conservation based on equation (2).Indeed, the tensormodifies the energy density of the EMF in the plasma, and this modification is not accounted for by the traditional concept of the energy density of a plasma’s collective motions.It was for this reason that our previous calculations helped to identify new terms in the wave drift equations.

The above suggests that natural oscillations in vector wave fields should be supplemented by forced oscillations even in the traditional analysis of the corresponding phenomena.

Albeit we do not need data onin the current research, some comments regarding these data are in order.

The rapid variation of the functionshould correspond to the exponentMeanwhile, the motive force that induces forced oscillations generally includes both a component that is in resonance with the natural oscillations under consideration and components that generate forced oscillations that are polarized as free oscillations in the remaining two degrees of freedom of the electric field oscillations in the given plasma.If we select inadequate initial field data in the corresponding components,we will get a pumping of the forced oscillations with rates that vary exponentially in time in accordance with the differences in natural frequencies between the current natural oscillation and the other branches of natural oscillations.Hence,it is only for carefully selected initial data ofthat the ‘amplitude’becomes a function with an appropriately smooth dependence on the time delayt−t′.In addition,the tensorshould be self-adjoint (recall property(5)).These features can be regarded to some extent as principles for selecting data for(Possibly, a deeper study of the problem will provide a more rigorous method for this selection.)

From the viewpoint of developing the wave kinetics, the most important part ofis the one corresponding to the component of the motive force that modulates the natural oscillations considered.It is structured similarly toin the sense of the tensor’s entry and exit.That is, we need the componentThe initial data for this component,should be equated to zero: another choice of these data implies redefining the initial spectral density of the wave

According to property(5),in the time domaint＜t′,the corrected leading order of two-time correlation function should be

The requirement that this corrected leading order should satisfy equations (6) and (7) defines the style of time transformations of the wave spectral density.We have found that structure (13) becomes an appropriate approximation of the real two-time correlation function in the time domaint＜t′when the rate of change of the wave spectral density obeys the equation

(See the derivations of this rate in [3, 13].) In this equation,the last two terms contain the convolutions of the tensorwith derivatives of the exit polarization tensorof the leading orderIn both our wave drift scenarios,they do not contribute to the wave kinetics, because the conductivity tensor is purely imaginary in cold plasmas.In addition,we consider non-relativistic plasmas,so that we can neglect tensor elements with subscriptsm≠0.Finally, the equation does not account for the linear growth or damping of the waves.In the physical situation of [3], it was absent, and in the one of [13], it was negligibly small.

The Laplace transform of the conductivity tensorσkωis defined as follows:

We note that it appears in our calculations due to the internal time integrations within equations (6) and (7) after the substitution of the leading order (11) of the two-point correlation function into these equations.That is,the Laplace transformation is not the basis for intermediate calculations in our approach.

3.Additional comments on the traditional kinetic models of wave drift

In previous studies by other authors, little attention has been paid to the distinction between purely potential waves and waves that have solenoidal components of the electric field.On the one hand,we are not aware of any models of wave drift in which the electric field in waves is not a potential one.On the other hand, existing rationales for traditional wave drift scenarios do not provide a proper analysis of the consequences of the distinction between purely potential waves and waves with nonzero solenoidal components in their electric fields.Speaking in terms of the above wave number densities()σ rNk, only equations of the type of equation (3) have ever been derived and generalized.It is likely that the equation for the drift of potential waves can always be reduced to an equation of this type.We have tested this suggestion by a special consideration of the drift problem of Langmuir waves in a cold non-magnetic plasma in its rest frame.For brevity, we will not present the corresponding calculations here.We only note that writing the results of these calculations in wave number densities reduces the wave drift equation just to an equation with the structure of equation(3).The reader may decide that this somehow justifies the special interest in the concept of wave action preceding the wave number density concept.

It is worth noting that our predecessors especially valued the concept of wave number density, considering its consistency with the understanding of quantum theory.Believing in its outstanding scientific importance, they used it as the basis to work out principles for modeling the kinetics of nonlinear plasma phenomena.In particular, some ‘golden rule’ was formulated (see, e.g., [49], page 23).The rule postulates that the collision integrals of nonlinear wave phenomena take symmetric forms in terms of wave number densities.This justified the logic in which the researcher calculated the ‘probability’ of a nonlinear phenomenon in some simple context and then generalized the collision integral by introducing the corresponding symmetric construct into its body.Meanwhile, this approach leads away from informative scenarios of nonlinear phenomena; for demonstrations of the rule failures, see [3, 12].Equally, the use of wave number densities cannot help in developing appropriately reliable scenarios of wave drift in the case of nonpotential waves.We analyze the distinctions of the corresponding scenarios in the next section.

4.Distinctions of informative scenarios of the drift of non-potential waves from traditional wave drift scenarios

Following our above statements, the kinetic equations of wave drift from[3]and[13]contain parts that extend beyond the Procrustean bed of traditional wave drift scenarios.The first natural step toward uncovering the reason for this is to translate the corresponding parts back into the language of spectral wave densities.

For electromagnetic waves in a cold non-magnetized plasma, our equation of drift in phase space is

Thus, the ‘protruding’ term of the equation is

Within the drift equation, in terms of spectral densitiesthe counterpart of this term is structured in the same way:

We dare say that this should originate from the terms that contain the spatial derivative of the wave polarization tensor.Considering equation (14), there is just a single term that survives in the limit of a cold non-magnetized plasma:

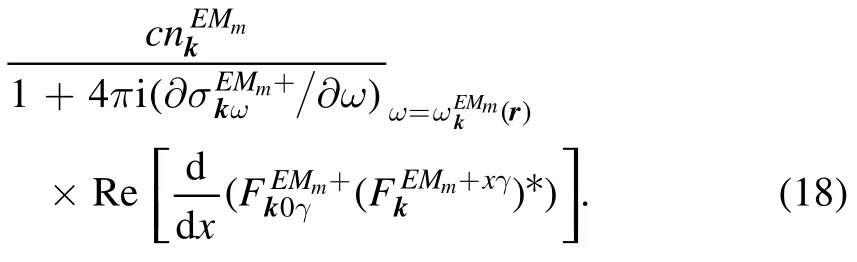
(For simplicity, we assume a slab plasma geometry, with the plasma density gradient directed along the x axis.) The electric field in the polarization tensor was defined by equation(32) in [3] (where, unfortunately, it was misprinted: the multiplier s on the right-hand side was omitted):

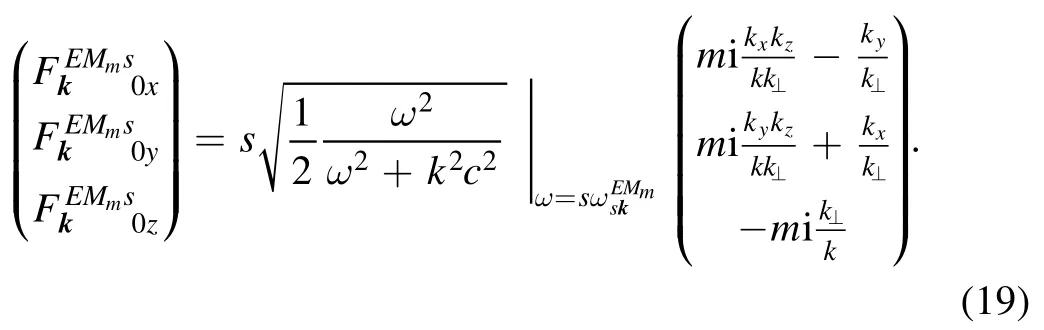
Here k⊥denotes the component of a wave vector that is orthogonal to the leading magnetic field.Regarding the wave’s magnetic field, the corresponding components of the wave polarization tensor can be easily expressed in terms of the electric components by the general formula

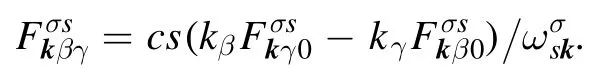
In view of the above data,the structureis trasnformed toIts spatial derivative is

Note also that

Thus, expression (18) becomes

which coincides with formula (17).

We note that it would definitely have been possible to separate the two branches of electromagnetic waves in a different way-the structure of intermediate calculations and the final relations do not depend on this.Having addressed ourselves to the formulae from paper [3], we have taken advantage of there being ready-made components for the current consideration.

Now consider the case of drift of long Langmuir waves in a cold magnetized plasma [13].We first clarify that in paper[13], waves with rather small wave vectors, k, were considered.That is,it was assumed that k was small compared to the following three characteristic inverse lengths: ωp/c,This was necessary to succeed in the analytical study of the problem.Let the first of the above restrictions be the most severe one.We note that in the limitk→0, the natural frequency of one of the branches of plasma waves takes the value ωp≈ωpe.With a decreasing external magnetic field, this branch is transformed into the branch of Langmuir waves, and it is the natural oscillations with wavenumbersfrom this branch that were considered in [13].Naturally, we called them the Langmuir waves.

For the above Langmuir waves, the ‘protruding’ term of the wave drift equation leads to the following piece of the rate of change of the wave spectral density (see formula (4.30) in[13]):

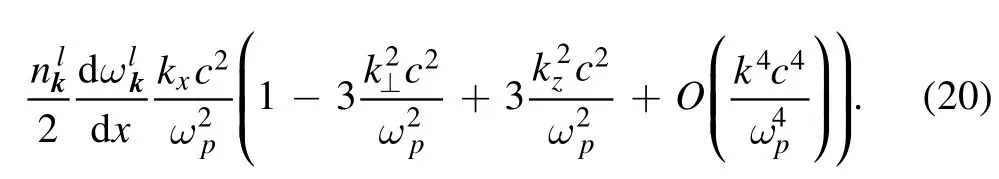
Again, in equation (14) there is only one term with the gradient of the polarization tensor that might have led to the above summand.It is

It can be calculated using the following formulas from [13]:

(the natural frequency of the Langmuir wave),

(the needed ‘electric’ components of the polarization tensor),

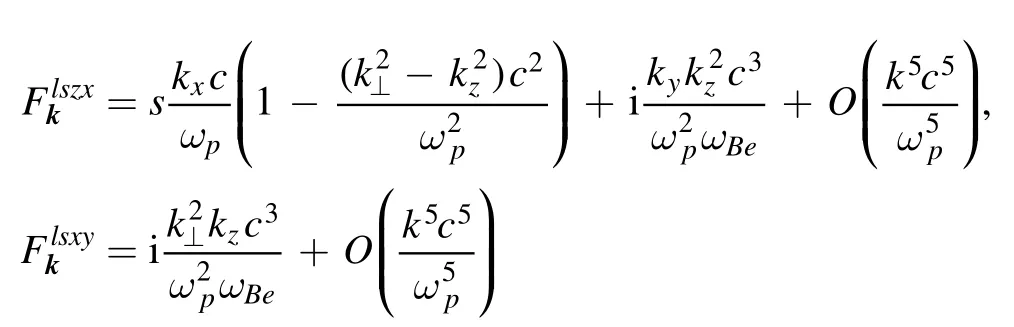
(the needed ‘magnetic’ components of the polarization tensor),

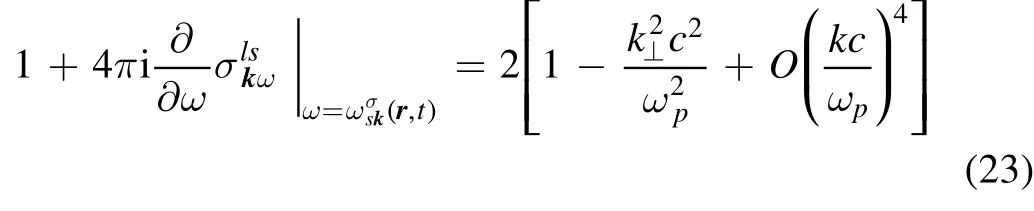
(a consequence of formula (4.23) from [13]).

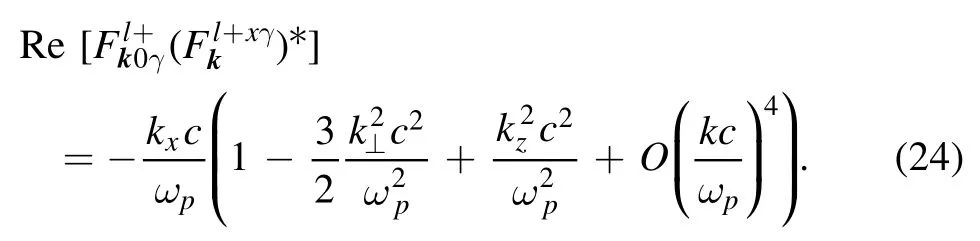
In the last two formulas, we have omitted unimportant terms that cannot distort the expression of interest within the accuracy of the corresponding equation of wave drift.

The substitution of expressions (24) and (23) into term (21) yields

(see formula(4.24) in [13]).Due to this, the term of interest takes the form of (20).

Thus, it is the spatial dependence of the polarization tensor that provides additional summands to the usual rates of change of the wave number density in both of our previous studies.

Analyzing the structure of the corresponding summands,we have found the following.In our paradigm of plasma wave kinetics,the contribution of waves with certainkandrto the Poynting vector is

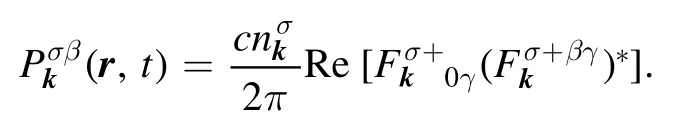
Note that this constitutes the full wave energy flux in both the situations considered; the fluxes of non-electromagnetic energy due to the coherent motions of charged plasma particles were negligible there.If the corresponding plasmas were homogeneous, the wave energy fluxescould be easily expressed in terms of the wave energy densities:

We would like to clarify the concept of forced oscillations a bit more.It was quite natural to formulate the idea of natural plasma oscillation (and, accordingly, the idea of a plasma wave) on the basis of considering a homogeneous plasma.It is also natural to seek to adapt the corresponding knowledge to the modeling of the wave field in a weakly inhomogeneous plasma, with the formation of wave packets from harmonics with close wave vectors.However,one must bear in mind that for non-potential waves, the spatial displacement of the wave packet in an inhomogeneous plasma leads not only to a change in the carrier wave vector and natural frequency of the packet, but also to a change in the relations between the components of the electric and magnetic fields in each of the packet harmonics.The latter certainly implies variations of the Poynting vector, which cannot but distort the usual continuity equation for the energy of the corresponding collective plasma motions.In other words, a simple superposition of natural oscillations in the case of a weakly inhomogeneous plasma cannot satisfy Maxwell’s equations.A natural solution to this problem is to supplement the natural plasma oscillations by forced oscillations.The latter can propagate in a plasma only in conjunction with natural oscillations.In this regard, we reiterate that we have found a trace of forced oscillations through the calculation of the kinetics of drift of specific non-potential waves,having no initial idea of these oscillations.

At this point,we comment again on the practice of using geometric optics to model wave fields.We reiterate that our calculations in[3,13]are based on more rigorous theory than those developed in geometric optics.We would like to emphasize that the most natural way to develop model scenarios of plasma physical evolution is to reduce the full plasma description to a simpler model of plasma kinetics and that such a reduction inevitably leads to a decrease in the informativeness of the scenarios.The reader is reminded again that our predecessors did not care about the loss of scenario informativeness in the processes of the corresponding reduction.In particular, the principles of geometric optics imply that a classical ionized plasma is undistinguishable in its physical manifestations from an unspecified plasma ensemble,and thus ignore an important reason for the loss in theory informativeness.(We reiterate that the conclusions about the mutual influence of the statistics of the system ensemble, which are usually interpreted as the real laws of the system’s physical evolution, strongly depend on the ensemble’s composition and,therefore,cannot objectively characterize the scenario of the system’s physical evolution.)

We also note that the ideas of geometric optics, as applied to a fully ionized plasma,stem from the belief that the collective motions of a plasma’s charged particles are governed by some mean field with a rather smooth dependence on the spatial position.Meanwhile, no scientifically sound recipe for specifying this field has ever been proposed.In an ionized plasma, a charged particle moves against the background of microfields of other charged particles, which in their effect significantly exceed the mean field that can be imagined for this plasma.Roughly speaking, averaging over voluminous spatial regions yields a correlation function of microfields that far exceeds the possible squared mean field.Understanding the latter was one of the reasons for the development of our two-time formalism and its further reduction to the description of plasma evolution in terms of functions of a single time variable.

Finally, the wave drift equation (14) does not depend on the intensities of the other waves present in the plasma.This,in particular, is evidence against the idea of channeling of wave action from the one branch of plasma oscillations to another in the wave drift phenomenon.

5.Conclusions

In this paper, we have again considered the problem of wave kinetics in inhomogeneous plasmas.We have found that the traditional kinetic equation of wave drift in normal space and wave vectors cannot adequately describe the drift of nonpotential waves.We have shown that redefining wave energy cannot help one to restore the applicability of this equation.We have deduced that the case of potential waves is likely to be the only one that might be adequately described by the usual kinetic equation of wave drift.We have also shown that the reason for the failures of the common wave kinetic equation was a lack of understanding that when plasma oscillations propagate in an inhomogeneous plasma, these oscillations are accompanied by forced oscillations.We have explicitly pointed out the terms in our kinetic equations of wave drift that embody the effect of these forced oscillations.

The understanding of wave drift in the phase space of an inhomogeneous ionized plasma that has been achieved cannot but question the modern practice of using geometric optics to model plasma wave fields.We suppose that it is the concept of the mean field that constitutes the defective postulate at the base of the latter; this concept underlies the wave description within geometric optics.As we stated above, research has never discussed the method of defining the mean field in the plasma.In our approach with averaging in the phase space over extensive regions of the plasma volume,the mean field is negligibly small.We have formed a wave drift picture through an analysis of the dynamics of the two-time correlation function.The latter takes into account the correlations of microfields in the plasma and not the spectrum of spatial harmonics of the problematic mean plasma electromagnetic field.

Our study was performed as part of the development of highly informative plasma kinetic scenarios.Its results illustrate once again the importance of considering physical phenomena with careful attention to the information aspect of their development.Arguing for some scenario of the physical evolution of a system,the researcher should bear in mind that unknown features of the system’s microstate lead to unpredictable variations in the tendencies of the evolution, which makes the scenario somewhat reliable at best for some finite time interval.This interval can be quite short or long enough(depending on the physical situation and the skills of the researcher), but it is always finite: the information content of the scenario inevitably does decay with time.(The obvious reason for the decay of information in our approach,with the averaging of the microdistribution over large regions in the phase space, consists in the never-ceasing exchange of these regions and their surroundings by charged particles.) In a sense,this feature has some overlap with Eddington’s concept of ‘time’s arrow’ (see [50], pages 68-69).At the same time,had one tried to develop a ‘reverse’ scenario of plasma evolution from later to earlier times, one would have again got the decay of information: the farther into the past, the lower the reliability of the plasma image that the researcher develops on the basis of the current macrophysical evolution of the plasma.

The above comments highlight the aspect of information content and its decay in physical scenarios in view of its particular importance for technological practices of mankind.

ORCID iDs

V I EROFEEV https://orcid.org/0000-0002-8223-7807