C语言程序设计循环结构之“四要素学习法”

摘要：C语言程序设计中循环结构是顺序、选择、循环三大基本结构之一，功能强大，使用灵活方便，但是学生学习难度比较大。该文以累加和为切入点深入分析循环结构特点，总结出循环结构“四要素学习法”，用for、while、do-while等循环语句分别实现其循环算法，并举例加以深入解读，使循环结构学习思路清晰，重点突出，对于学生掌握并灵活使用循环结构非常有帮助。

关键词：C语言程序设计;循环结构;四要素学习法

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2020）29-0121-03

1 背景

C语言是面向过程的高级程序设计语言之一，它具有数据类型丰富、灵活高效和结构化等特征[1]。C语言程序设计是自动化等工科专业非常重要的专业课程，尤其后期学习单片机时进行编程也是使用C语言。循环指事物周而复始地运动或变化。在计算机程序设计中，“循环”这一术语指的是一种专门的控制结构。特征是重复执行循环体中的语句，比一般情况下的顺序执行复杂一些，需要跳转命令和条件判断组合实现[2]。循环结构是C语言程序设计中三大基本结构之一[3]，也是最为重要、使用频率较高的结构，其特点是，在给定条件成立时，反复执行某程序段，直到条件不成立为止。循环结构一直是学生学习程序设计的一个难点，下面笔者就以循环结构中的累加和问题S= 1+2+3+…+100为切人点，谈一下自己的授课经验。

累加和的实现有2种方案。

解决方案1：考虑顺序结构来完成，虽然可以实现，但是比较烦琐，费工，计算机智能化快速化优势并没有体现出来，同时顺序结构算法的通用性太差，题目稍有变化如从1加到1000等，就不能解决了。也就是说，顺序结构来解决重复才做问题，只能具体问题具体分析，不能解决此类问题。

解决方案2：使用循环结构实现，程序代码简单，逻辑清晰，而且通用性强，可以推广到类似的其他问题。

比较两种方案，循环结构用来解决重复性操作问题优势明显，但是循环结构算法相对来说比较难掌握。笔者也就此算法进行了深入的课堂教学研究，从操作过程拆解、循环结构流程图和循环语句实现三方面来进行分析讲解，提出了循环结构的“四要素学习法”。

2 循环结构教学过程

2.1 操作过程拆解

对于累加和问题，本质上是相加操作的重复，所以其共性为：和=操作数1+操作数2，重复若干次;重复性相加操作的不同之处在于：每次参与相加的操作数1和操作数2是不同的，操作数1为上次相加之和，称为旧和，操作数2为上次操作数2加l之后的值。对比重复性操作的共性和不同之处，累加和操作问题的通式可写为：新和=旧和+操作数2。所以累加和问题就变为：设置好初值，利用变量值可变的特性重复求和，直到加到100，累加结束。在此过程中，设累加和存放在变量sum中，操作数2为变量i，则初值设定为sum=0，i=1，重复相加通式为：sum=sum+i，累加完成后i值增1，此后进行下一次累加操作，知道i值超过100，累加结束，共重复100次，此过程即为循环结构。

对于程序设计当中涉及重复性问题，都可按照这个分析过程来进行初步分析。

2.2 循环结构四要素

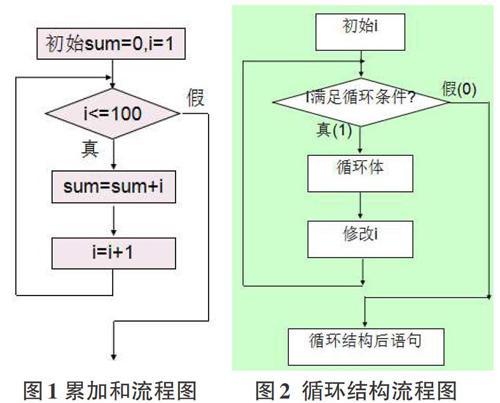
以上分析内容用程序流程图表示如下图1。通过对循环结构流程图的分析可以看出，循环结构的实现需要注意四个关键点：1）初值设定，是循环正确开始的基础;2）循环条件，限定重复性操作重复执行的条件，也是循环能适时终止的保证，避免循环陷入死循环;3）循环体，是循环重复性操作的具体体现;4）循环变量的调整，是循环体正确执行或者循环次数控制的重要环节。在使用循环结构时，这四点必须予以重视。

由累加和问题推广到一般重复性问题，流程图如图2所示。在分析一般的具有重复性操作的问题时，都可以归结为以上四要素的分析推理过程，所以在C语言程序设计中循环结构这一环节的授课过程中，笔者提出了“四要素学习法”，结合重复性操作问题的特点，找出重复过程中的四个方面，即起始特点、重复操作条件、重復操作本身以及每次重复操作的细微调整，对应以上讲解的循环结构实现过程中的初值设定、循环是否执行的判断条件、循环体及循环变量调整四个要素，循环结构算法即可实现。

2.3 循环语句实现

循环结构的实现语句包括三种：for、while、do-while，三种语句虽然语法规则不同，但都可实现上面的循环结构，而且按照四要素法来分析这三种循环语句，都包含前面所分析的循环初值设定、循环判断条件、循环体及循环变量调整四个要素其中。

1）for语句实现

for语句使用十分灵活，变化多端，可以通过for语句培养灵活使用C语言的能力[2]，故我们首先以for语句为例来设计循环结构程序代码。

for语句的基本格式为：

for（表达式1;表达式2;表达式3）

循环体语句;

其执行过程为：先执行表达式1，再判断循环条件表达式2是否成立，如果条件成立则执行循环体语句，执行完循环体语句后执行表达式3;之后再次判断循环条件是否成立，若条件还成立，则继续重复循环体语句，当条件不成立时则跳出for循环。

累加和for语句实现的程序为：

for（i=l，sum=O;i<=lOO;i++）

sum=sum+i;

用四要素学习法分析for语句程序段：

i=1.sum=0;为循环初始条件;i<=100为循环判断条件;sum=sum+i;为循环体语句;i++;为循环调整语句。

2）while语句实现

while语句在单片机程序设计中常会使用，基本格式为：

while（循环条件）

（循环体语句;）

其执行过程为：先判断循环条件是否成立，如果成立就执行循环体语句，执行完毕后再回来判断循环条件是否满足，如此重复;直到条件不成立时，跳出循环，执行while循环后边的语句。在使用while的循环语句时一定要包括能最后判断出while循环语句条件的真假性的操作过程Ⅲ。

用while语句实现累加和问题：

i=l.sum=0;

while（i

（

sum=sum+l;

i++;

）

同样用四要素法分析while语句程序段：

i=1，sum=0;为循环初始条件;i<=100为循环判断条件;sum=sum+i;为循环体语句;i++;为循环调整语句。

3） do-while语句实现

do-while语句的特点：

do-while语句的一般形式为：

do

循环体语句;

while（循环条件）;

其执行过程为：首先无条件地执行一次循环体，然后判断循环条件是否成立，成立则继续循环，否则退出循环。因此，与while循环相比，do-while循环要无条件执行一次循环语句，实现相同算法时要注意此区别。

用do-while语句实现累加和问题：

i=l.sum=0;

do

{

sum=sum+1.

}while（i<=100）;

再次用四要素法分析do-while语句程序段：

i=1，sum=0为循环初始条件;i<=100为循环判断条件;sum=sum+i为循环体语句;i++为循环调整语句。

4）三种循环语句对比

由以上分析可知，不论是什么语句来实现循环结构，都离不开循环结构的四要素：循环初值设定、循环判断条件、循环体和循环变量调整，循环算法才能正常实现，否则循环有可能出现起始条件不正确，或者陷入死循环等难以发现的逻辑问题。三种语句的区别只在于四要素在循环算法中的位置不同。所以，可以把循环四要素法推广应用到重复性操作所有问题中。在设计循环结构的算法时，关键在于设置好循环四要素，循环算法才能成功实现。同时也可以利用四要素法来验证循环算法是否能成功实现要求。

3 循环结构四要素学习法应用

接下来进行应用循环四要素学习法来实现其他循环问题案例分析。

例题1：求费波那西（Fibonacci）数列的前40个数。这个数列同时也是一个有趣的数学问题，可把数列问题描述为：最开始有一对兔子，从出生后第3个月起每个月都能生一对兔子。小兔子长到第3个月后又可以每个月生一对兔子。假设所有兔子都不死，则每个月的兔子总数满足费波那西数列的规律。

根据前面分析信息可总结出这个数列有如下特点：第1、2两个数为1、1。从第3个数开始，该数是其前面两个数之和。即：

用程序的思想来解读这个数学问题，用循环结构实现最为恰当。其思路为：设置两个数列变量fl和f2用来暂存数列当中的某两个数，设置一个循环调整变量i，从数列第一个数到数列中的第40个数。由式1可知当i=1和i=2时，f1=1，f2=1。本问题中i的值每变化一次，F。就要重新赋一次值，故重复性操作为Fn=Fn-1+Fn-2（n≥3）并输出显示。在数列前两个数都为1的基础上，循环变量的值从i=1到i=38才能把数列前40个数计算卅来。所以用循环四要素法来解读：循环初值为f1=1，f2=1，i=1;循环判断条件为i≤38;循环体语句为Fn=Fn+1，+Fn-2（n≥3）和显示语句，并且要为下次Fn的赋值做准备，即进行fl和f2值的调整;循环变量调整则为i值每次增1。算法流程图如下图3所示。

用for语句实现费波那西数列循环结构，其程序代码为：

#include

int main0

f int fl=l，f2=l，f3; int i;

printf（”%12d＼n%12d＼n”，f1，f2）;

for（i=l;i<=38;i++）

f f3=fl+f2;

printf（”o-/012d＼n”，f3）;

fl=f2;

f2=f3：

）

return 0：

）

接下来进行案例二的分析。

例2：用;π/4≈1-1/3+1/5-1/7+…公式求仃的近似值，直到某一项的绝对值小于10^-6为止（该项不累计加）。

由题十信息可知，公式有无穷项相加减，明显可考虑用循环结构来实现。分析题中所给公式的特点可总结为：

1）每一项的分子都是1，后一项的分母是前一项的分母加2;

2）相邻两项项分数的符号正负交替;

故相邻两项数据的关系为：1/n=>1/n+2

在设计程序时，需要用到几个变量：flag：符号变量，用以进行每次加减运算时符号的替换;pi：π变量;n：参与运算的每一项的分母值;t：由符号变量除以没意向的分母值得到参与运算的当前项。用循环四要素法来解读：循环初值为flag=l，pi=0，n=1，t=1;循环结束条件为某一项的绝对值小于l0-6，故判断条件为t≥l0^-6;循环体：计算pi值;循环变量调整：n=n+2，flag取反以及t的新值计算。程序流程图如图4所示。

程序清单如下：

#include

#include

int main0

{ int flag=l; double pi=O，n=l，t=l;

while（fabs（t）>=le-6）

（ pi=pi+t;

n=n+2：

flag=-flag;

t=flag/n;

）

pi=pi*4;

printf（”pi= o-/010.8f＼n”，pi）;

return O：

）

4 结束语

由以上分析可知，重复操作性问题利用循环结构可使程序结构清晰，语句简洁。循环结构设计过程中一定需要注意四要素：初值设定、循环判断条件、循环体、循环变量调整，只要把握住这四个要素，循环结构设计就可实现，并且也可易用循环四要素查找循环结构是否存在漏洞。同时在算法设计好之后，程序实现时也应注意for、while、do-while等循环语句的使用特点，在合适的位置上设置合适的四要素。所以利用“四要素学习法”来讲解循环结构，简单易懂，重点突出，对学生熟练掌握和应用循环结构解决程序问题可起到事半功倍的效果，循环类问题就可轻松解决。

参考文献：

[1]姚立新，梁宏涛.C语言程序设计[M].北京：电子T业出版社，2013：1.

[2]方悦.循环、迭代与递归[J].电脑知识与技术，2020，16（6）：55-57，66.

[3]谭浩强.C程序设计[M].北京：清华大学出版社，2010：124.

[4]高茂嬋，吕雪，彭星星，等.浅谈C语言中循环结构程序设计[J].电脑知识与技术，2020，16（6）：58-60.

【通联编辑：谢媛媛】

作者简介：陈丽敏（1982-），女，河南许昌人，讲师，硕士，研究方向为检测技术与自动化装置。