高校网络环境中的网络安全态势感知系统

摘要:校园信息化建设在我国取得了长足进展,网络攻击也越来越多。该文将基于Markov博弈的网络安全态势感知方法引入到高等院校的网络安全实践中。利用Markov博弈模型分析网络威胁的传播过程,并给出量化的安全态势评估。实验证明NSSAMG算法能够很好地定量描述网络威胁的严重程度。态势评估结果有助于合理实施安全加固方案,提高了系统的安全性。
关键词:Markov博弈;网络安全态势感知;零和博弈;校园网络
中图分类号:TP393 文献标识码:A
文章编号:1009-3044(2020)29-0072-03
计算机网络越来越广泛地运用于高校的校园管理和教学事务中。校园内外大量复杂的信息交流,日益复杂的网络结构,各种新型网络攻击手段层出不穷。传统的入侵检测系统无法完全监控和防御网络攻击行为。引入网络安全态势感知( network security situation awareness,NSSA)十分有必要。
网络态势是指有各种网络设备运行状况、网络行为以及用户行为等因素所构成的整个网络当前状态和变化趋势[1]。网络安全态势感知(NSSA)指对网络安全要素进行获取、理解、显示和预测。NSSA的研究一般集中在网络安全状态的图形化呈现[2]、量化评估[3]和数据融合[4l三方面。
本论文将Markov博弈模型运用到高校校园网络安全态势感知研究中,对校园网进行网络安全评估,并对评估结果展开分析。
1 网络安全态势感知
态势感知分成4个步骤:数据采集、态势理解、態势评估、态势预测。网络系统数据包括网络结构、资产、脆弱性、威胁等等。态势理解和评估的过程应当简洁明了,便于实现,满足实时性要求。态势感知结果应当直观地展现给用户,满足用户的多种需求。最后能提供加固方案(防御措施)供管理员参考实施,以提高网络安全性。
NSSA系统在网络中部署多个传感器,采集网络信息进行数据融合并汇总,利用这些信息构造数学模型,用数学方法精确描述网络系统的安全态势和变化趋势,并给出网络安全加固方案。
2 Markov博弈理论
Markov博弈理论是博弈理论和Markov过程结合。网络安全的案例中,攻击方和网络防御方展开博弈。攻击方的目的是窃取信息、瘫痪网络服务、窃取网络资源。防御方的目的是保护机密信息,维护网络服务正常运行,防止网络资源被盗用。一方的收益就是另一方的损失,所以双方展开双人零和博弈。
这里利用Markov决策过程(Markov Decision Process,MDP)网络安全系统在考虑网络攻击者策略的同时,采取策略使网络受的威胁最小。这里用1表示网络安全系统,2表示网络攻击者。所以博弈均衡点上的网络安全评估值为:
3 基于Markov博弈理论的网络安全态势评估算法
基于Markov博弈理论的网络安全态势评估算法(NSSAMG算法)
输入:数据采集模块检测到的各类安全数据
输出:量化的网络安全态势
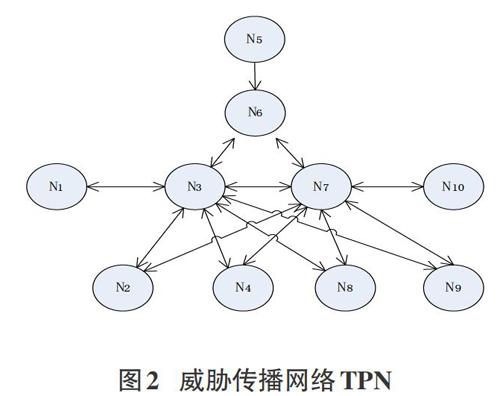
1)依据网络结构对传感器收集网络数据进行数据融合,得到各个网络节点的信息。对每个不同的安全威胁t建立威胁传播网TPN(t)。
2)根据TPN(t)建立Markov博弈模型,rIPN(t)中的每个节点的状态近似为一个Markov状态。利用公式(2)和公式(3)计算路径中各个网络节点(状态)的保密性、完整性、可用性的威胁值,评估t的安全态势。
3)利用公式(4)制定针对t的网络安全加固方案。
4)将威胁集合中所有威胁的保密性、完整性、可用性损害分别求和,分别得到三方面的安全评估。
5)运用加权模型评估网络的整体安全态势。
在该算法的第2步中采用公式(2)进行有限次数的迭代运算。第4步中将集合中的损害分别采用指数求和的方法求和,而不是简单的线性求和。指数求和公式是:
4 实验分析
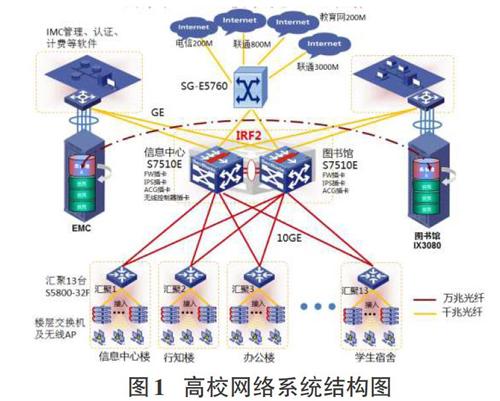
这里给出网络安全态势感知系统在高校网络中应用的范例,其网络结构如图所示,校园内外由防火墙隔开,内部由两台核心交换机组成了链路备份,并连接各部门和单位的局域网。态势感知系统首先在网络节点上部署传感器(软件或硬件),对各台主机和服务器进行恶意代码和脆弱性检测。根据收集的信息融合得到了资产集合、威胁集合、脆弱集合,建立TPN。
利用传感器收集的数据设置网络节点的信息,用六元组来表示,例如(N6,5,5,3,0,1)表示节点N6的ID名、保密性等级、完整性等级,可用性等级、是否被感染、是否可能受到威胁。威胁传播路径TPN由被感染网络节点的六元组序列按顺序构成。利用NSSAMG算法计算各节点在各个状态下受到的威胁度,得到最优化加固方案,再根据网络管理员事先制定的具体加固方案进行加固。
这里用模拟实验对NSSAMG算法的性能进行评估,并与未考虑威胁传播的态势感知方案进行比较。模拟实验中的折扣系数口取0.8,网络威胁传播概率取0.4。初始的威胁节点是(Ns,0,5,5,1,1)。
图3中展示了大约25个迭代周期中网络系统安全态势的变化情况。当没有采用NSSAMG算法时,系统仅仅记录威胁不断扩散的情况,最终所有网络节点都被恶意程序感染,网络受到的威胁值高达33左右。如果采用NASSMG算法,Markov博弈算法计算状态后续可能的威胁行为和加固行为带来的影响,所以当关键的网关节点遭到网络威胁时,NSSAMG给出了较高的威胁评估值。而随着威胁以一定的概率扩散,NSSAMG给出对应的加固方案,把网络威胁值控制在一个较为稳定的范围内。网络状态进入稳定状态,网络安全评估值稳定在8.5左右。
5 结束语
本文将基于Markov博弈的网络安全态势感知方法引入到高等院校的网络安全实践中。网络攻击者和网络安全防御方进行双方零和博弈,以此分析网络威胁的传播过程,并给出最佳加固方案。实验证明NSSAMG算法能够很好地定量描述网络资产的价值和网络威胁的严重程度。态势评估结果帮助合理实施安全加固方案,提高了系统的安全性。
参考文献:
[1] Seddigh N,Pieda P,Matrawy A,et aI.Current trends and advanc-es in information assurance metrics[C]//Proc.of the 2nd AnnualConf. on Privacy,Security and Trust.2004:197-204.
[2] Lau S.The spinning cube of potential doom[Jl.Communicationsof the ACM,2004,47(6):25.
[3] Chen X Z,Zheng Q H,Guan X H,et aI.Quantitative hierarchicalthreat evaluation model for network security[J].Journal of Soft-ware,2006,17(4):8 85- 897.
[4] Steinberg A N,Bowman C L,White F E.Revisions to the JDL data fusion modeI[C]// SPIE. Proc. of the Sensor Fusion: Archi- tectures, Algorithms, and Applications, SPIE 3719. Orlando: SPIE, 1999.
[5] Sutton R S,Barto A G.Reinforcement learning:An introduction[M].2nd ed.MIT press,2018.
[6] Panin A,Shvechikov P,Practical Reinforcement Learning[D].Coursera and National Research University Higher School ofEconomics,2017.
[7]邱锡鹏,神经网络与深度学习[M].Github Inc,2018.
[8] GB/T 20984-2007.lnformation security technology-Risk as-sessment specification for information security[S].General Ad-ministration of Quality Supervision,lnspection and Quarantineof P.R.C,2007(in Chinese).
【通聯编辑:谢媛媛】
作者简介:宣慧(1979-),女,江苏南京人,工程师,硕士,研究方向为计算机应用和网络安全。

