巧用拼图实验感悟数形结合

焦倩玉

苏科版初中数学教材七年级下册第九章“整式乘法与因式分解”中，一个非常重要的思想是用不同的方法计算同一块图形的面积，那么它们是相等的。通过这个思想推演证实了这一章的法则和公式。课标要求学生能推导乘法公式（a+b）（a-b）=a2-b2，（a±b）2=a2±2ab+b2，了解公式的几何背景，能利用公式进行简单计算;反过来，也能利用公式法进行多项式的因式分解。

“整式乘法与因式分解”这一章中，“整式乘法”和“因式分解”是两种互逆变形，“整式乘法”的最终结果是“和”的形式，“因式分解”的最终结果是“积”的形式，学生容易混淆。

笔者在学生完成此章的学习之后，开展了一节拼图实验的教学，期望学生通过拼图实验，探索拼图与整式乘法、因式分解之间的内在关系，弄清这两种变形的互逆关系及各自的功能，进一步体会数形结合的思想方法，发展几何直观和推理能力。

一、教学实录

实验工具：A型纸片（边长为a 的正方形）、B型纸片（边长为b 的正方形）、C型纸片（长为a、宽为b 的长方形）各若干。

1.操作与发现。

用1张A型纸片、1张B型纸片、2张C型纸片拼成如图1的正方形。计算整个图形的面积。

于是，可得整式乘法（a+b）2=a2+2ab+b2，因式分解a2+2ab+b2=（a+b）2。

将1张B型纸片按如图2的方法放置于1张A型纸片上。计算阴影部分的面积。

生1：阴影部分面积是大正方形面积剪去小正方形面积，即a2-b2。

生2：把未被覆盖部分剪开（如图3），重新拼图。这个新的长方形的面积为（a+b）（a-b）。

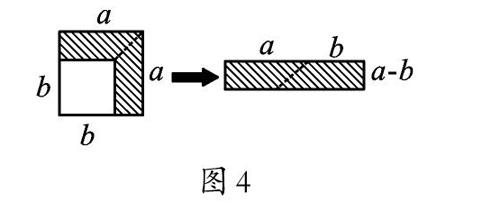
生3：把阴影部分剪成两个一样的梯形（如

图4），每个梯形的上底是b，下底是a，高是（ab），总面积是（a + b ）（a - b ）2·2=（a+b）（a-b）。

于是，可得整式乘法（a+b）（a-b）=a2-b2，因式分解a2-b2=（a+b）（a-b）。

【教学说明】课标要求学生借助图形直观发现整式乘法，了解公式的几何背景。借助图形直观，经历“由形到数”，学生易于发现结论。使用不同的方法计算同一个图形的面积，分别对应“整式乘法”结果“和”的形式和“因式分解”结果“积”的形式

2.操作与思考。

用1张A型纸片、4张B型纸片、4张C型纸片拼成一个正方形。计算它的面积。

生4：因为要拼一个正方形，所以它的长和宽应该相等。我将唯一的A型纸片放在左上角。跟A连接的只能是C，它们都有共同的边a，所以我分别在A的右侧和下侧放了一张C，于是就发现此时的右下角缺了一个边长为b 的小正方形，自然需要放一张B型纸片。现在我还剩下2张C型纸片和3张B型纸片，重复刚刚的过程，在这个新的正方形右侧和下侧放一张C，最后再把剩余的3张B型纸片补上就好了。

师：说得非常清晰！拼图的关键是相互连接的边长度相同。

由这个拼图，可得整式乘法（a+2b）2=a2+4ab+4b2，因式分解a2+4ab+4b2=（a+2b）2。

取1张A型纸片、2张B型纸片、若干张C型纸片，使其拼成一個长方形。计算它的面积。

师：这与上一题有什么不同之处？

生5：我们不知道C型纸片的具体数量。

生6：虽然题目的条件没有说，但是由于A型纸片和B型纸片的边长都不相等，所以无法连接。只能在空白处补上3张C型纸片。

由这个拼图，可得整式乘法（a+b）（a+2b）=a2+3ab+2b2，因式分解a2+3ab+2b2=（a+b）（a+2b）。

分别取若干张A型、B型、C型3种纸片，使其拼成一个长方形，并计算（a+b）（a+3b）。

师：读完题后，你有什么想法？

生7：要计算（a+b）（a+3b），表明这个长方形的长为a+3b，宽为a+b。跟上一个拼图相比，宽不变，长多了b，再在右侧添加1张C型纸片和1张B型纸片。

于是，得到整式乘法（a+b）（a+3b）=a2+4ab+3b2。

分别取若干张A型、B型、C型3种纸片，使其拼成一个长方形，并将多项式a2+10ab+9b2 分解因式。

师：你可以不用动手拼图就得到答案吗？

生8：（a+b）（a+9b）。我发现这3道题的多项式分别为a2+3ab+2b2、a2+4ab+3b2、a2+10ab+9b2，观察得到ab 项的系数都比b2项的系数大1。而这个矩形的长每增加b，C型纸片和B型纸片同时增加，保持C型纸片一直比B型纸片多一张。

师：非常棒！他已经自觉地将数和形结合起来看了，关注到了多项式的系数与拼图之间的联系。

于是，得到因式分解a2+10ab+9b2=（a=b）·（a+9b）。

【教学说明】在操作与思考中设置了4个不同的问题。问题1明确纸片数量，要求拼一个正方形。问题2需要学生自己确定纸片的数量拼一个长方形。这两个问题都是“由形到数”。问题3计算两个多项式相乘，这两个多项式分别对应长方形的长和宽。问题4将一个多项式分解因式，这个多项式每一项的系数对应不同类型纸片的数量。这两个问题都是“由数到形”。

3.拓展与延伸

有A 型纸片、B 型纸片、C 型纸片各10 张。从中取若干张纸片（每种纸片至少取1张），把取出的这些纸片拼成一个正方形（所拼的图中既不能有缝隙，也不能有重合部分）。你觉得可以拼出多少种不同的正方形？

（小组讨论，成果汇报。）

问题的关键是使用的3种类型的纸片中，使用最多的同一种纸片不能超过10张。假设a 的系数为m，b 的系数为n，使用完全平方公式将（ma+nb）2 进行展开，得到m2a2+2mnab+n2b2，分别观察a2、ab、b2 的系数m2、2mn、n2，只要它们小于等于10即可。故按顺序找出6种情况如下表：

【教学说明】拓展与延伸对学生提出了更高的要求，即不动手拼图，只借助多项式的系数和不同类型纸片之间的对应关系得到结果。由于纸片的数量是有限的，这就限制了多项式的系数的大小。再融合分类讨论的思想，有逻辑地列出问题的完整答案。

二、教后反思

笔者引导学生利用3种不同类型的纸片拼图，再现整式乘法与因式分解的情境。笔者通过弱化条件或改变条件与结论，问题设计层层递进，引发学生深入思考。随着纸片的数量不断增加，学生可以发现：如果给定数量的纸片能够拼成一个矩形，那么从整体和部分两个角度计算这个图形的面积可以得到一个整式乘法公式，同时与纸片面积一样的多项式就能分解因式。学生感悟数量关系与图形性质的相互转化，加深了对拼图与整式乘法和因式分解之间关系的理解。

“让学生获得适应未来生存与发展所必需的数学活动经验”是义务教育阶段数学课程的目标之一。数学活动经验只有个体在亲历数学活动的过程中才能获得。在本节数学实验课中，学生不断从事拼图、计算面积等活动，通过独立思考、合作交流，并辅以归纳总结和提升，有助于自身基本活动经验的形成。总之，数学实验本质上是一种解决问题的活动。教师是活动的组织者、引导者与合作者，学生才是活动的主人。要想学生真正参与到数学活动中来，教师要精心设计实验，让学生在探索中获得真知，体会学习数学的快乐。