混凝土损伤对节制闸闸室体系可靠度的影响

楚万强 秦净净,2

（1.黄河水利职业技术学院 水利工程学院， 河南 开封 475000； 2.开封市软基工程结构分析评价工程技术研究中心， 河南 开封 457000）

0 引言

我国大部分水闸建于20 世纪60-70年代，水闸在服役期间，闸基的土质参数、水位参数等是依赖于时间参数的随机变量，闸室体系的可靠性呈现一个动态变化过程[1-3]。同时，由于混凝土材料的高离散型，宏观上表现为材料特性的统计涨落，在广义荷载效应作用下，材料内部结构发生损伤并演化进而影响结构安全运行[4-5]。因此，为使这种不确定在机理上更符合实际实际情况，有必要在水闸体系可靠度分析中考虑损伤效应。

损伤因子法计法目前主要应用于重力坝稳定可靠度分析[6-7]，而此方法在水闸工程中的应用较少。为此，本文基于损伤理论，在水闸闸室常规可靠度分析中考虑混凝土损伤劣化对材料性能的影响，引入损伤因子，建立混凝土损伤后的剩余强度概率模型，探讨闸基土质参数变异敏感性，以期更能符合实际工程，研究成果可为在役水闸的安全评定、加固决策以及寿命预测提供理论依据。

1 工程实例

某开敞式节制闸，闸室顺水流方向长12m，底板厚1.0m，上下游端各设置一个深0.7m 浅齿墙。闸室为5 孔，闸孔总净宽15m，每孔净宽3m，边墩厚0.7m，中墩厚1.0m。闸墩顶部高程68.86m，闸墩上部设置排架，排架高度3.5m，排架上设置工作桥和启闭机房，交通桥布置在闸室下游侧，桥面净宽4.5m，总宽5.1m，检修便桥布置在闸室工作桥上游侧，总宽1.4m，净宽0.8m，钢筋混凝土板式结构。

1.1 计算参数

本文不考虑浪压力、泥沙压力及地震作用，取水闸结构自重、闸室上下游水压力、闸底板与地基间的摩擦力、地基粘聚力、地基基承载力为随机变量，参数统计如表1 所示。

表1 随机变量参数统计

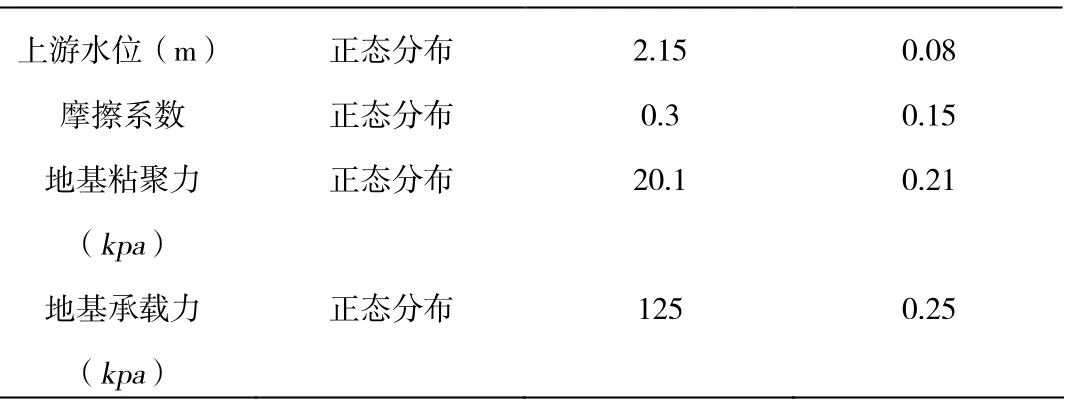
上游水位（m） 正态分布 2.15 0.08 摩擦系数 正态分布 0.3 0.15 地基粘聚力（kpa） 正态分布 20.1 0.21 地基承载力（kpa） 正态分布 125 0.25

1.2 闸室体系可靠指标

用Monte-carlo 法编制程序计算正常蓄水情况下四种单一失效模式可靠度指标，将四种失效模式视为串联系统，利用PNET 法得到体系可靠度指标，见表2。该闸为一级建筑物，闸室按第二类破坏对待，对应二类破坏βT=3.7，对应pf=1.08×10-4。由表可以看出，水闸系统失效概率略高于目标失效概率，满足要求；若考虑水闸闸室各单元间联系、灌缝等因素, 水闸的结构体系可靠指标将有更大幅度增加。

表2 闸室可靠度计算结果

1.3 混凝土不同程度损伤对闸室可靠度指标的影响

根据河海大学断裂与损伤课题组研究[12]，混凝土指数函数损伤模型参数如下D0=0.05，Df=0.1，εf=0.9×10-4，εu=6.87×10-4，B=3.85，C=1.25，在不考虑混凝土损伤时产生的水压力对水闸闸室的影响的情况下，4 种失效模式可靠度指标随混凝土损伤程度的变化见图1-4。由图可知，4 种失效模式可靠度指标均随混凝土损伤程度的增加而减小；当损伤由D=0.05 增加到D=0.5，闸基抗滑稳定可靠度指标由3.76 降至3.17，坝趾抗压强度可靠度指标值由4.12 降至3.59，坝踵抗拉强度可靠度指标值由4.47 降至3.92，上下游应力比 可靠度指标值由3.86 降至3.21，其中，上下游应力比对损伤因子变化最敏感，因为混凝土损伤相当于对水闸又加载了一个水压力，上下游应力比波动更大；在损伤D＜0.1 时，混凝土损伤发展很慢，四种失效模式的可靠度指标相较无损伤下降的比率小，在在损伤D＞0.1 时，损伤发展速率很快，四种失效模式的可靠度指标比无损伤下降的比率大，说明水闸建成初级阶段所形成的初级损伤对闸室体系可靠度指标影响小，随着水闸的运行，混凝土损伤加大，可靠指标不断下降。

图1 闸基面抗滑可靠度指标随损伤程度的变化

图2 坝趾抗压强度可靠度指标随损伤程度的变化

图3 坝踵抗拉强度可靠度指标随损伤程度的变化

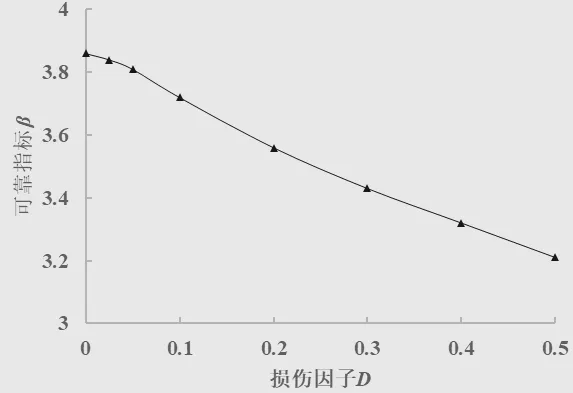
图4 上下游应力比可靠度指标随损伤程度的变化

1.4 材料变异性对闸室体系可靠度的影响

变异系数在概率统计中反映了一个变量的离散程度，变异系数不同，得出的可靠指标有差异。变量摩擦系数、粘聚力的随机特性对失效模式的可靠性指标影响甚大，是影响水闸稳定的关键参数，因此，考虑损伤变量为随机变量时，取均值为0.35，变异系数为0.1，并假设其为正态分布，对摩擦系数、粘聚力不同均值和不同变异系数对闸室体系可靠度指标的影响见表3、4 所示。

表3 不同摩擦系数、粘聚力均值的闸室体系可靠度指标Tab.3 Reliability index of the lock chamber system with different friction coefficient and average value of cohesion

表4 不同摩擦系数、粘聚力变异系数的闸室体系可靠度指标Tab.4 Reliability index of lock chamber system with different friction coefficient and cohesion variation coefficient

从表3、4 可以看出，考虑损伤后，随着摩擦系数和粘聚力的变化结构体系的可靠指标相比不考虑损伤时均下降，且变异系数越大，两者相差的趋势越明显；材料均值的变化对可靠指标的结构体系可靠度计算结果影响不显著，但是材料的变异系数发生微小变化时，可靠指标的计算结果会发生较大的变化，且变异系数越大，可靠指标越小，其中粘聚力变异系数的变化对可靠指标的影响大于摩擦系数。因此，粘聚力变异系数属于敏感因素，在实际工程中应谨慎取值、论证合理。

2 结论

本文基于可靠度理论和损伤力学概念建立闸室混凝土的一般损伤演变模型，为水闸闸室的寿命评估提供一个新思路和方法，并探讨损伤因子对四种失效模式的影响以及材料变异性对闸室体系可靠度影响，得出以下结论：

（1）混凝土的初级损伤随水闸运行性能影响小，但随着混凝土损伤累积，水闸闸室体系可靠指标逐渐减小，后期应进行混凝土的加固。

（2）闸基摩擦系数和粘聚力的均值对闸室体系可靠度指标影响微小，但粘聚力的变异系数是敏感因素。