基于沙壤土黏粒量预测土壤水分入渗量和湿润锋深度

夏 天，田军仓,

（1.宁夏大学 土木与水利工程学院，银川 750021；2.宁夏节水灌溉与水资源调控工程技术研究中心， 银川 750021；3.宁夏旱区现代农业水资源高效利用教育部工程研究中心，银川 750021）

0 引 言

【研究进展】土壤水分入渗最精确的定义即“水分通过土表进入土壤的过程”[1]，是自然界水文循环的重要环节。土壤水分入渗特性不仅受土壤质地、结构、含水率和有机质量等理化特性的影响，也会直接或间接地受到外界因素的影响[2]。土壤水分入渗问题的研究可为地表径流、水土流失、含水层补给、灌溉用水管理和作物可利用有效水提供重要依据[3]。为此，国内外学者开展了大量的理论和试验研究。理论研究主要是针对各种入渗模型的研究，入渗模型主要分为3 类，即物理模型、半经验模型和经验模型[4]。物理模型，其理论依据是达西定律和质量守恒定律，主要有Green-Ampt 模型[5]，Philip 模型[6]和Richards 方程[7]。半经验模型基于一些简单的假定，主要有Horton 模型[8]和Singh 等模型[9]。经验模型则以野外和室内观测数据为基础，主要有Kostiakov 模型[4]和改进的Kostiakov 模型[10]。试验研究方面，主要针对土壤质地[3,11-14]、结构[3,11,15]、体积质量[3,11,16-17]、有机质量[18-19]、含水率[20]、温度[21-22]和碎石土中碎石量和直径[23-25]等因素对土壤入渗特性的影响进行了研究。土壤质地是不同粒径固相颗粒即黏粒（＜0.002 mm）、粉粒（0.002～0.02 mm）和沙粒（0.02～2 mm）量的配合比，文献[11-12，26]将黏粒量作为反应土壤质地的指标，研究了土壤的入渗特性。其中，文献[11]针对不同土质，通过大田积水入渗试验，得到了黏土黏粒量与稳渗率之间呈幂函数负相关关系。文献[12]针对不同土质，通过大田积水入渗试验，得到了黏粒量与吸湿率、稳渗率之间均呈对数函数负相关关系。文献[26]采用来源不同、粒径范围不同的土样配制合成土壤，通过室内模拟试验，得到了在概化体积质量一致的条件下，合成土壤的黏粒量与稳渗率之间呈幂函数负相关关系。【切入点】从数据拟合的角度来看，采用幂函数和对数函数进行拟合，虽能获得较高的拟合优度，但是从物理含义的角度考虑，采用上述2 种函数形式均会导致黏粒量趋于0 时吸湿率或稳渗率发散，不符合实际入渗过程。

【拟解决的关键问题】针对上述问题，本研究采用黏粒质量百分比不同的沙壤土，通过室内土柱积水入渗模拟试验，得到在干体积质量一致的条件下，利用黏粒量预测土壤入渗量和湿润锋深度的模型，以期为沙壤土入渗特性的预报提供理论依据。

1 材料与方法

1.1 供试土样

供试土样取自宁夏银川市北部唐来渠畔贺兰县四十里店村耕作农田，取样地块面积约0.267 km2，取样深度0～20 cm。为了使所取土样具有代表性，沿该地块的长对角线方向等间隔取8 份土样，取样间隔9 m。将所取的8 份土样自然风干、晾晒、碾压并过2 mm 筛后混合均匀，并随机取样，测定初始含水率和颗粒粒径分布。初始质量含水率在105 ℃条件下恒温烘干至土样质量为恒质量时测定。颗粒粒径分布采用Bettersize-2003 型激光粒度分布仪测定，土壤质地分类采用国际制。原状土的干体积质量采用环刀（体积96.6 cm3）法测定。测定时，土壤的初始含水率、颗粒粒径分布和干体积质量结果均为3 次重复测量的平均值。测得土样的初始含水率为3.25%，黏粒（<0.002 mm）的质量分数为8.83%，粉粒（0.002～0.02 mm）的质量分数为11.82%，沙粒（0.02～2 mm）的质量分数为79.35%，质地为沙壤土，干体积质量为1.41 g/cm3。

1.2 试验设计和土样制备

采用人工合成的方法制备试验用沙壤土。为了保证土颗粒得到充分筛分，采用8411-型电动振筛机，以0.074 mm 为筛底，将供试土样按照粒径＜0.074 mm和0.074～2 mm筛分为2个组分，记为组1和组2。每次筛分质量为200 g，筛分时间设定为1 h。待土样制备量达到试验所需后，将组1 和组2 土样分别混合均匀，并测定各组的颗粒粒径分布，结果见表1。

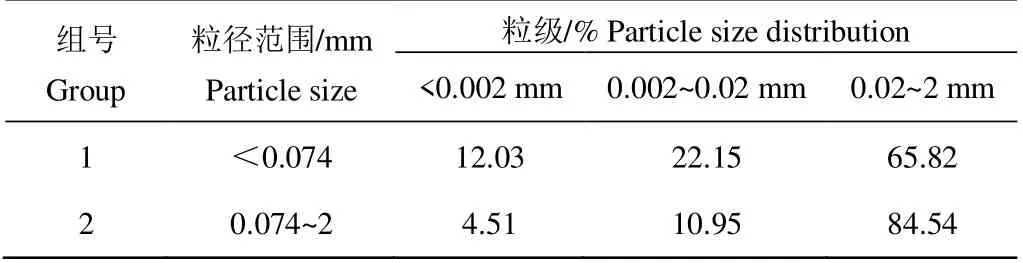
表1 颗粒粒径分布 Table 1 Particle size distribution

将组1 和组2 的土样进行混合，设计11 种不同的质量比处理（记为S1—S11），相应的组1 和组2质量混合比和颗粒粒径分布见表2。

1.3 试验装置

试验装置由供水马氏瓶和土柱及连接部件组成。供水马氏瓶为内径7 cm，高100 cm 的透明亚克力圆筒；土柱为内径7 cm，高50 cm 的透明亚克力圆柱，底部设排水孔，呈蜂窝状布置。马氏瓶固定在高度可调的支架上，土柱固定在不锈钢铁架台上，二者通过橡胶软管连接。为方便读取试验数据，马氏瓶和土柱侧壁均设有刻度线。

表2 试验处理 Table 2 Experimental treatments

1.4 土样装填

试验在宁夏大学土木与水利工程学院土壤物理实验室内进行，平均室温为26 ℃。土样装填前，在土柱内壁均匀涂抹1 层白凡士林，防止边壁效应对水分入渗产生影响，在土柱底部填放滤纸，防止土颗粒流失。由于合成土壤的各组分来源相同，故其装填体积质量与原状土的干体积质量相同，即1.41 g/cm3。土样装填时，采用电子天平秤取每2 cm 厚土层所需土样质量，无损倒入土柱，并用夯土板夯实至相应刻度线处，层间打毛以保证相邻土层充分接触。土柱装填总高度为45 cm。装填结束后，在土表铺设滤纸防止注水过程中表层颗粒受到强烈冲刷。

1.5 观测内容及步骤

采用一维垂直积水入渗试验测定合成沙壤土的入渗特性，水头5 cm，每个处理重复3 次。观测内容包括：不同时段的湿润锋运移深度和累积入渗量。观测步骤：试验开始前，记录马氏瓶初始液面位置。试验开始后，记录湿润锋每推进1 cm 所需时间，马氏瓶每次冒泡结束后记录相应时间和液面位置，待入渗速率基本不随时间变化时终止试验。数据处理和图像绘制采用Origin 2017，数据统计采用SPSS 22.0。

2 结果与分析

2.1 不同处理沙壤土湿润锋运移深度

S1—S11 处理沙壤土的干体积质量相同，黏粒和粉粒百分量依次增加，沙粒量依次减少，构成了一个质地由粗到细的系列。不同处理沙壤土湿润锋运移深度随时间的变化如图1 所示。入渗初始阶段，各处理湿润锋运移速率较大，颗粒组成对湿润锋运移深度变化的影响不明显。随着入渗的进行，颗粒组成对湿润锋运移产生显著影响，表现为随黏粒量增加，湿润锋运移速率减小，到达同一深度所需时间增长。黏粒量从4.51%增加至12.03%，湿润锋运移至土柱底部所需时间由103 min 增加至310 min，增幅为2 倍。

“如果将常委会机关视作动车，那么每个委室、每项工作都是一节车厢。为每节车厢装上党建‘发动机’，使党建工作与依法履职有机结合、协同发力，有效解决了党建工作和业务工作脱节问题，形成了全员参与、全员共建的良好党建格局。”市人大常委会副秘书长、机关党委书记王增宝说。

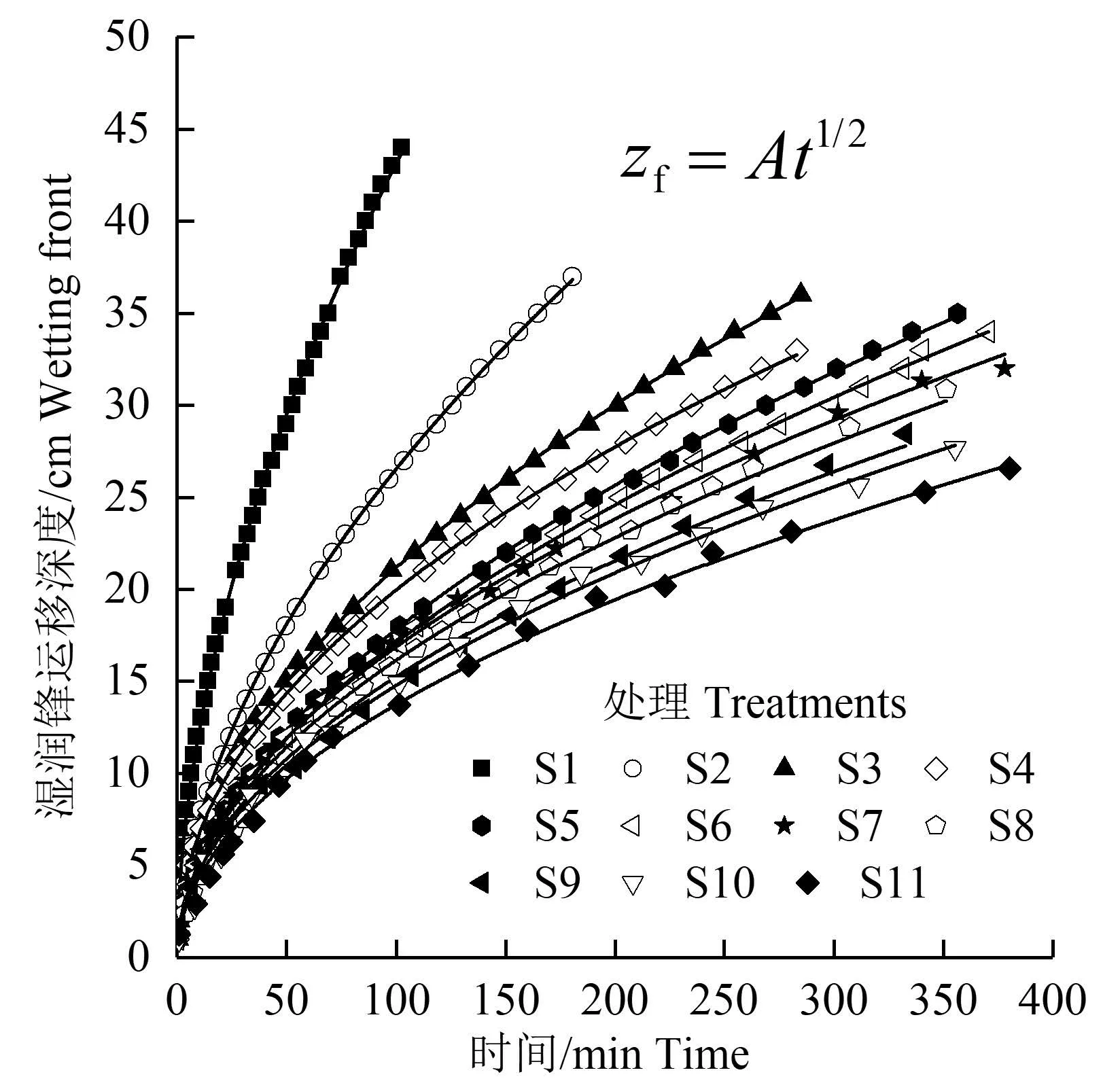
图1 不同处理沙壤土湿润锋运移深度随时间的变化 Fig.1 Wetting front versus time for different sandy loam soils

采用Philip[6]垂直入渗方程幂级数解的第一项对图1 中各处理湿润锋运移深度随时间变化的实测结果进行拟合，其表达式为：

式中：zf为湿润锋运移深度（cm）；t 为入渗历时（min）；A 为经验系数。拟合结果见表3。

表3 湿润锋运移深度随时间变化拟合结果 Table 3 Fitting results of wetting front versus time

由表3 可以看出，各处理拟合优度R2均在0.99以上，且统计分析结果表明，在p=0.01 的显著性水平下，各处理的回归效果显著。表明采用Philip 垂直入渗方程幂级数解的第一项可以很好地描述本试验条件下沙壤土湿润锋运移深度随时间的变化。

从表3 可以看出，随着黏粒（<0.002 mm）量增加，经验系数A 呈减小趋势，二者之间的关系绘于图2。

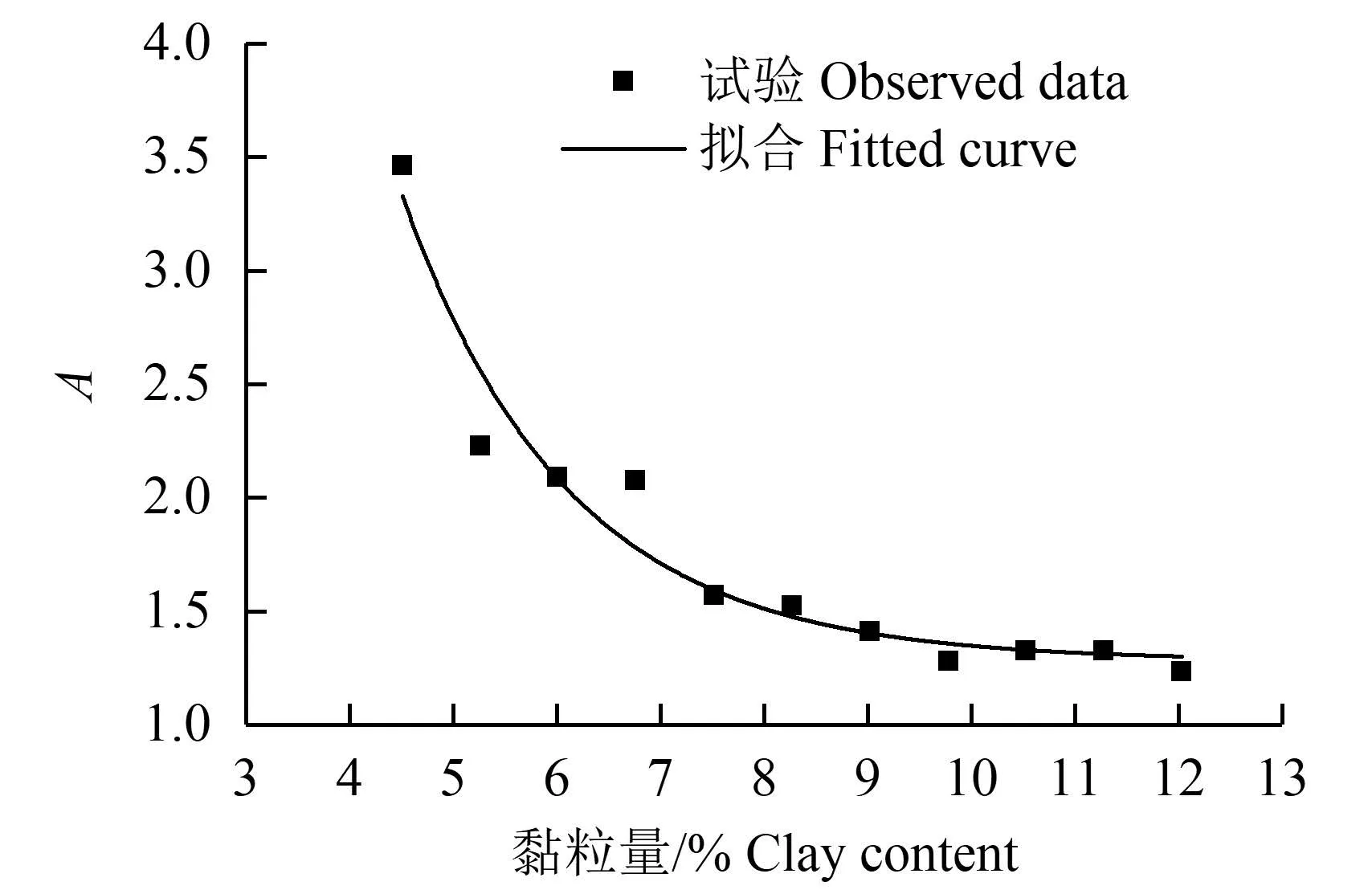
图2 系数A 和黏粒量的关系 Fig.2 Relation between coefficient A and clay content

采用指数函数对经验系数A 和黏粒量x 之间的关系进行拟合，拟合结果如式（2）：

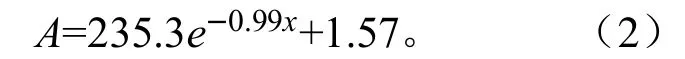
拟合优度R2=0.981，且在p=0.01 的显著性水平下，回归效果显著。表明黏粒量对湿润锋运移深度随时间变化模型经验系数A 影响显著，采用指数衰减模型可以很好地描述它们之间的关系。将式（2）代入湿润锋运移深度随时间变化的式（1）中，即得到了利用黏粒量预测湿润锋运移深度随时间变化的模型，如式（3）所示：

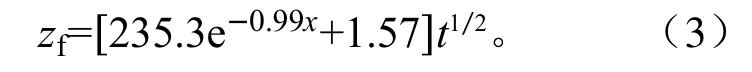
借助该模型，可快速推求已知黏粒质量百分数的沙壤土湿润锋运移深度随时间的变化。

2.2 不同处理沙壤土累积入渗量

不同处理沙壤土累积入渗量随时间的变化如图3所示。

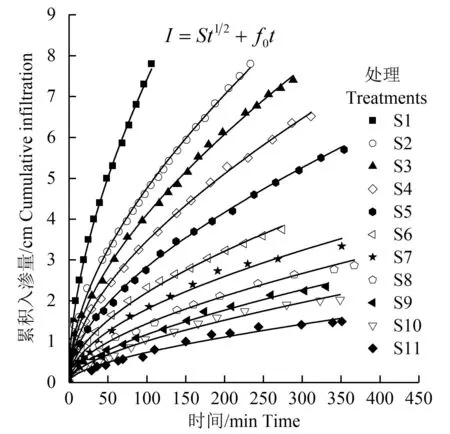
图3 累积入渗量随时间的变化 Fig.3 Cumulative infiltration versus time

从图3 可以看出，各处理土壤入渗率随时间的变化趋势相似，入渗初始阶段，入渗率较大，随着时间推移，入渗率逐渐减小，最终趋于稳定。黏粒量对累积入渗量影响显著，表现为相同入渗时间内，累积入渗量随黏粒量增加而减小。黏粒量从4.51%增加至12.03%，达到相对稳定的入渗速率时沙壤土累积入渗量由8 cm 减小至1 cm，减少87.5%。

采用Philip[6]入渗模型对图3 中各处理累积入渗量随时间变化的实测结果进行拟合，其表达式为：

式中：I 为累积入渗量（cm）；t 为入渗历时（min）；S 为吸湿率；f0为稳渗率（cm/min）。拟合结果见表4。

表4 累积入渗量随时间变化拟合结果 Table 4 Fitting results of cumulative infiltration versus time

由表4 可知，各处理拟合相关系数均在0.98 以上，且在p=0.01 的显著性水平下，各处理的回归效果显著。表明采用Philip 模型可以很好地描述本试验条件下沙壤土累积入渗量随时间的变化过程。

根据表4 的拟合结果，以黏粒（<0.002 mm）百分量作为反映土壤质地的指标，将各处理相应的吸湿率S 和黏粒量之间的关系绘于图4，稳渗率f0和黏粒量之间的关系绘于图5。

采用指数函数对吸湿率S 和黏粒量x 之间的关系进行拟合，拟合结果如式（5）：

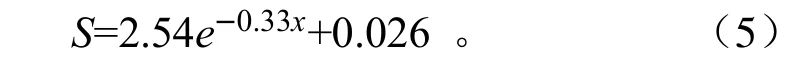
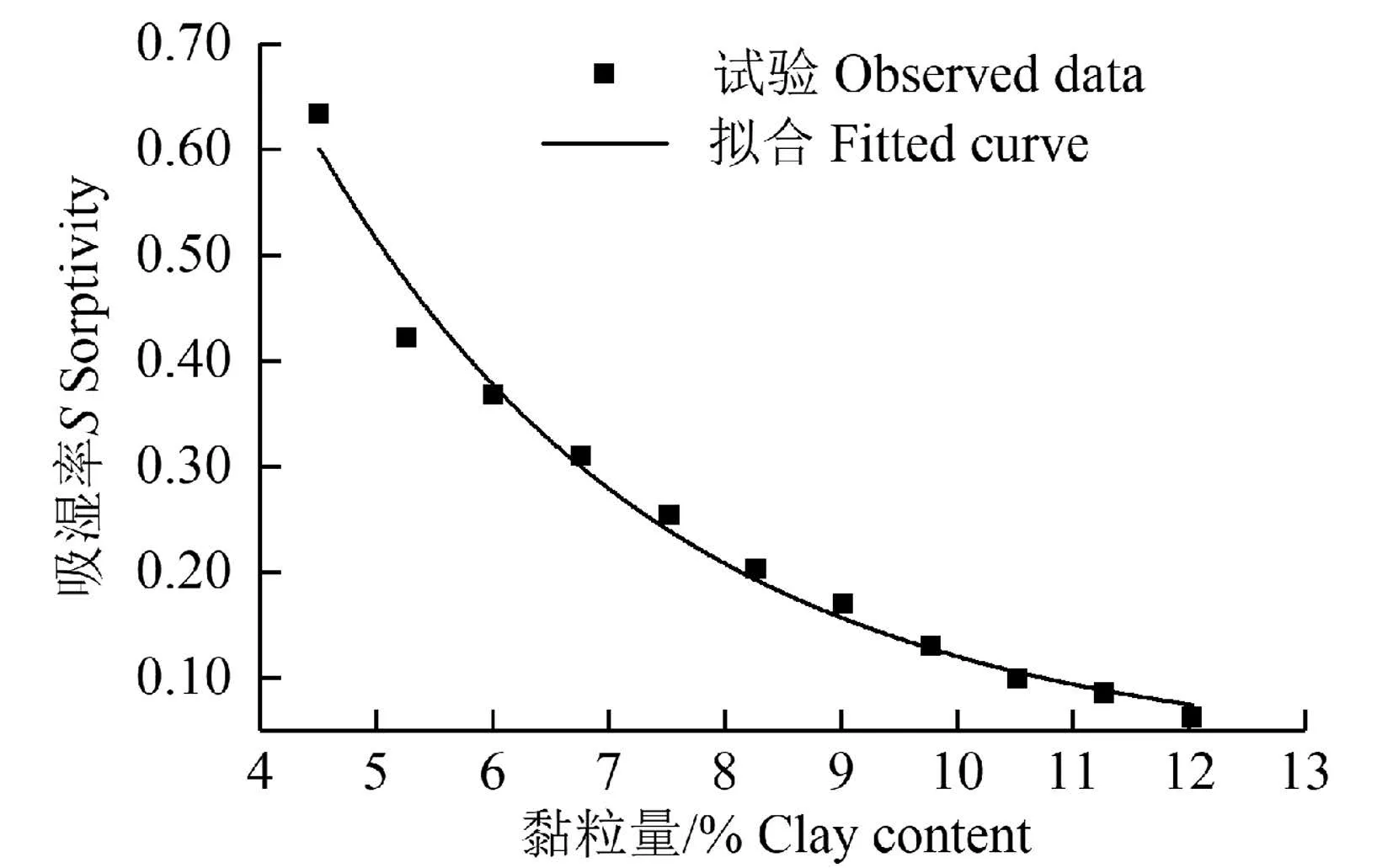
图4 吸湿率和黏粒量的关系 Fig.4 Relation between sorptivity and clay content

拟合优度R2=0.984，且在p=0.01 的显著性水平下，回归效果显著。表明质地因子即黏粒量对吸湿率S 影响显著，采用指数衰减模型可以很好地描述二者之间的关系。

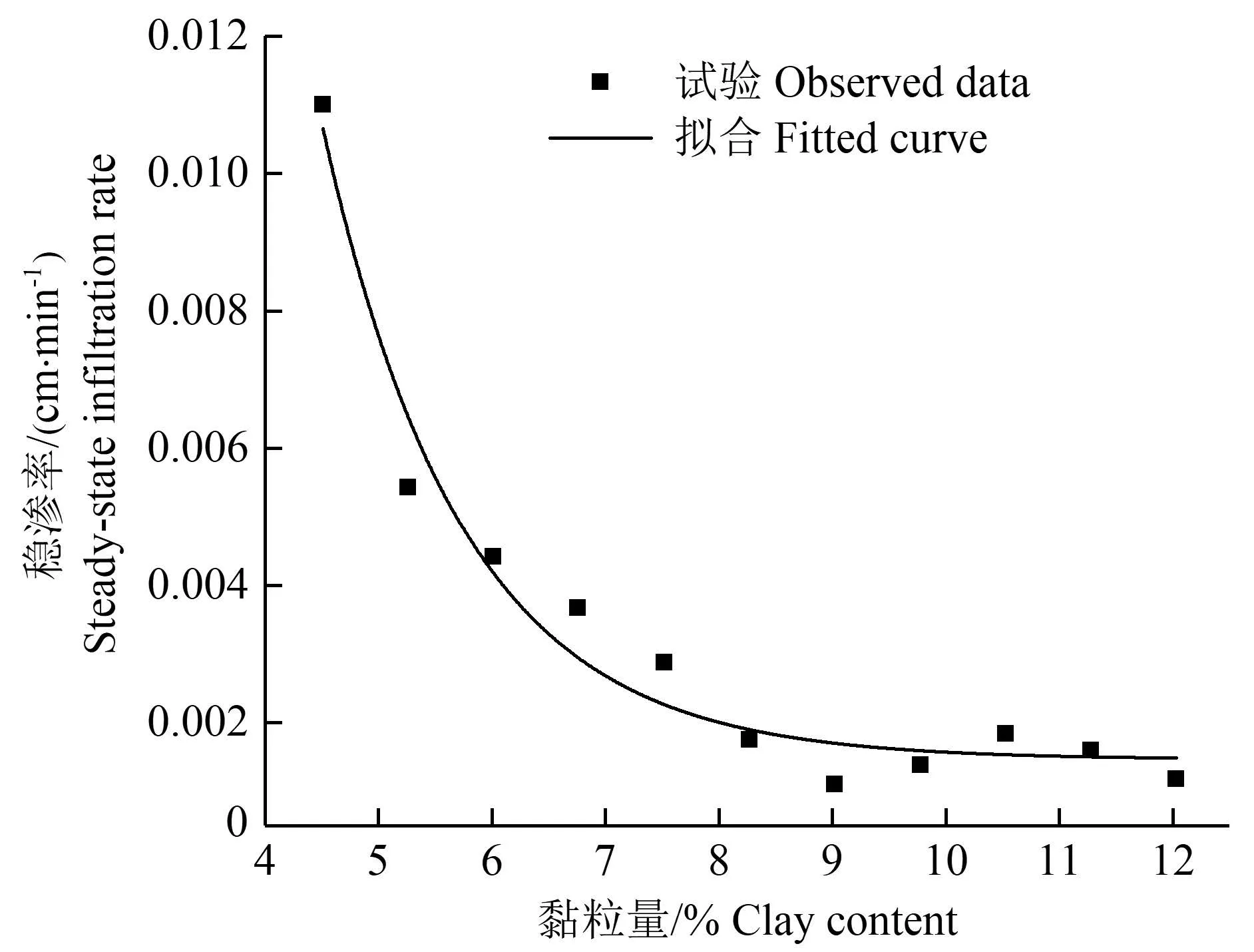
图5 稳渗率和黏粒量的关系 Fig.5 Relation between steady-state infiltration rate and clay content

同样地，采用指数函数对稳渗率f0和黏粒量x 之间的关系进行拟合，拟合结果如式（6）：

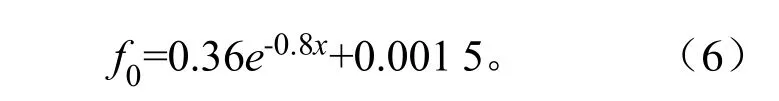
拟合优度R2=0.968，且在p=0.01 的显著性水平下，回归效果显著。表明质地因子即黏粒量对稳渗率影响显著，采用指数衰减模型可以很好地描述二者之间的关系。

将式（5）和式（6）代入式（4）中，即得到了利用黏粒量预测累积入渗量随时间变化的模型，如式（7）所示：

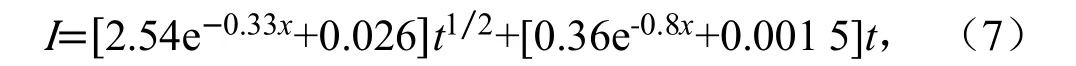
式中：x 和t 意义同前。借助该模型，可快速推求已知黏粒量的沙壤土累积入渗量随时间的变化。

2.3 模型验证

在原供试土样取土地块随机取土（0～20 cm），测得该土样黏粒（<0.002 mm）的质量分数为4.9%，粉粒（0.002～0.02 mm）的质量分数为13.63%，沙粒（0.02～2 mm）的质量分数为81.47%。对该土样进行室内积水入渗试验，试验方法和步骤同S1—S11 处理，并将该试样对应的黏粒量分别代入式（3）和式（7）中，预测湿润锋运移深度和累积入渗量，并与实测值进行对比，如图6 和图7 所示。通过对预测值和实测值之间的绝对误差进行计算，得到的结果为：90%的观测点其湿润锋深度预测值和实测值之间绝对误差均小于10%；91.7%的观测点其累积入渗量预测值和实测值之间绝对误差均小于10%。表明利用黏粒量预测湿润锋运移深度和累积入渗量的预测模型能够较好地预测该代表性地块沙壤土的湿润锋运移深度和累积入渗量。

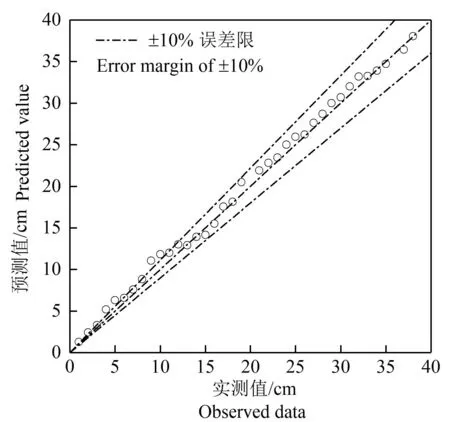
图6 湿润锋运移深度预测值和实测值的关系 Fig.6 Relation between observed and predicted value of wetting front distance

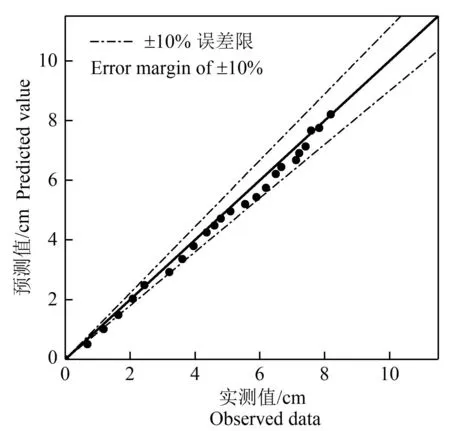
图7 累积入渗量预测值和实测值的关系 Fig.7 Relation between observed and predicted value of cumulative infiltration

3 讨 论

各处理沙壤土的吸湿率S 和稳渗率f0均随黏粒量增加而减小。从数据拟合的角度出发，我们均采用了指数函数对吸湿率S 和稳渗率f0与黏粒量之间的关系进行了拟合，并获得了很高的拟合优度（R2＞0.968）。文献[12]采用对数函数对吸湿率、稳渗率和黏粒量之间的关系进行拟合，文献[26]采用幂函数（幂指数为负值）对稳渗率和黏粒量之间的关系进行拟合，均获得了较高的拟合优度。但从物理意义上来讲，采用上述2 种函数形式拟合，均会导致黏粒量为0 时相应的入渗参数即吸湿率和稳渗率发散，而采用指数函数形式拟合则不会出现此问题，更加符合入渗的实际物理过程。

稳渗率f0理论上等于传导区的导水率[27]。本试验中，各处理土壤体积质量、孔隙率、初始含水率和入渗水头均相同，黏粒量将成为影响稳渗率最为活跃和主要的因素。随着黏粒量的增加，土壤颗粒变得更加细小，在总孔隙率一定的条件下，细小孔隙数量增加，大孔隙数量则相应减少，入渗水流过水面积减小，孔隙弯曲程度变得复杂，水分运移阻力增大，土壤的导水能力下降即导水率减小，则稳渗率f0减小，且随黏粒量增加这种减小的趋势愈加明显。本文得到了利用沙壤土黏粒量预测土壤入渗量和湿润锋深度的模型，但利用黏壤土黏粒量预测土壤入渗量和湿润锋深度是下一步的研究方向。

4 结 论

1）干体积质量为1.41 g/cm3条件下，黏粒量从4.51%增加至12.03%，沙壤土湿润锋运移至45 cm深度处所需时间由103 min增加至310 min，增幅为2倍；达到相对稳定的入渗速率时沙壤土累积入渗量由8 cm减小至1 cm，减少87.5%。

2）沙壤土湿润锋运移深度随时间变化模型经验系数、累积入渗量随时间变化模型中吸湿率和稳渗率均与黏粒量呈指数衰减关系，拟合优度均大于0.968。得到的利用沙壤土黏粒量预测土壤入渗量和湿润锋深度的模型具有较高精度，能够快速预测沙壤土入渗量和湿润锋深度，预测值与实测值之间绝对误差小于10%。