沿程加热式气泡泵最佳热流密度预测
段文利 杨洪海 张田田 司钰文
东华大学环境科学与工程学院
0 引言
气泡泵是无泵制冷循环中的动力之源,仅仅靠一根垂直管内生成的气液两相流动就可以为整个循环提供驱动力,将制冷剂从低位储液器提升到高位储液器,如图1。由于此特性,气泡泵具有低品位能源(太阳能、废水余热等)驱动,无活动部件,系统相对稳定,噪声低的优点。因此,气泡泵受到国内外学者的关注。

图1 气泡泵运行原理的示意图
气泡泵根据加热方式可以分为沿程加热式气泡泵和底部加热式气泡泵,相对沿程加热式气泡泵,底部加热式的研究更多。以底部加热式气泡泵为研究对象,Marcus Pfaff[1]从制冷系统的热力学角度对气泡泵进行分析,发现加热功率对气泡泵的效率影响甚微。而Benhmidene[2]搭建DAR 制冷系统实验台,通过研究20-200W 下加热功率对于气泡泵的影响,认为加热量是影响气泡泵性能的重要参数之一。A.Koyfman[3]设计了连续的气泡泵实验装置,实验发现加热功率是决定气泡泵性能的主要参数之一。另外U.Jakob[4]与N.Ben Ezzine[5]认为热流输入形式对于气泡泵性能有很大影响。汤成伟[6]通过实验研究了气泡泵的启动时间随压力的变化情况,发现加热功率对于液体提升量和稳定性有很大影响。Soo W.Jo[7]建立三维物理模型,利用CFX 模拟软件研究氨水在气泡泵的气液两相流动情况。
从流动和传热角度分析,沿程加热式气泡泵内气液两相流动更加复杂,整根垂直管管壁都会产生气泡,沿着上升过程不断聚合、冷凝湮灭,流态更加复杂。从大量的文献中可以看出,加热量是影响气泡泵运行最主要的因素之一。另外,沿程加热式气泡泵的实验研究中,保温极其困难,实验难度极大。所以,研究沿程加热式气泡泵多采用模拟研究。但是一般的数值模拟只是在某工况下进行,有确定的进口流量和加热量,而气泡泵实际运行中的进口速度与加热量存在耦合关系,单纯在某个工况下的模拟结果很难指导实际问题。所以,本文在课题组前期实验研究基础上[8-9],以水为工质,采用CFX-19 模拟软件研究加热量与进口流量之间关系。
1 控制方程
模拟研究气液两相流动的求解模型有均相流模型,分相流模型,漂移流模型和两流体等模型,模型由简到繁,求解由易变难,但是求解的准确性越来越高,所以采用两流体模型[10]。
采用两流体模型,关键需要湍流方程封闭,解决此封闭模型需要:相间动量,相间能量,相间质量传输模型及壁面沸腾模型。由于双流体模型所涉及的方程数量很多,为节省计算成本,通常采用迭代算法,即先求解动量方程,然后在此基础上求解其他方程。因此动量方程的准确性就直接或间接地决定了整个数值计算结果的准确性。
1.1 相间动量传输方程
气液两相间的动量运输表示为界面力的形式,界面力包括曳力FD和非曳力,其中非曳力包括升力FL、壁面润滑力FW和湍流耗散力FTD等。单位体积内两相间总的作用力为以上力之和,取l 或v 分别表示液相和气相:
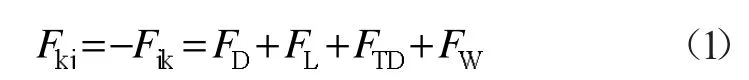
式(1)中右侧各项参照文献[11-12]推荐公式计算。
1.2 相间质量传输方程
在气泡泵中气相由液相汽化产生,液相只要达到运行压力下的饱和温度即可产生气泡,反之冷凝。假定气相在两相流中始终处于饱和温度,传热传质发生在气液两相的界面上。质量传输有用户自定义质量传输,质量传输选择热相变模型,并给定其饱和温度。单位体积内相间传质速率表示为:
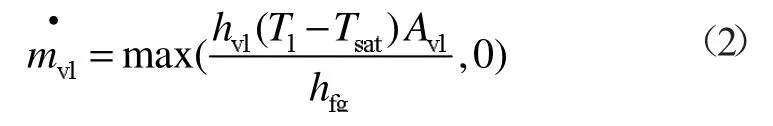
式中:Avl表示气液两相界面面积;Tsat表示饱和温度;hvl为气液两相界面处焓值。
1.3 相间能量传输方程
气液两相间的质量,动量和能量都是通过两相界面进行传递,由于产生的气泡弥散在液相中,因此将气相看作离散相,液相看作连续相。界面传热模型选用Two Resistance Model 模型。连续相选择Ranz-Marshall 模型,离散相选择zero resistance 模型。Ranz-Marshall 的关系式为:

式中:Re 为雷诺数;Pr 为普朗特数。
1.4 壁面沸腾模型
ANSYS CFX 采用Kurul 等提出的壁面热流分配模型,即伦斯勒理工模型(RPI:Rensselaer Polytechnic Institute)[13],模型对汽化核心密度、气泡脱离直径、气泡脱离频率、气泡等待时间等进行了描述。通过固体壁面传递给流体的总热流量Qwall分为三部分:对流传热QF,淬冷传热QQ及蒸发传热QE。

2 数值求解
由于所研究的气泡泵为垂直圆管的形状,相对于中心线轴对称,可以假定在圆周方向上物性参数梯度为零。另外,为了减少网格数量,降低计算量,将取1/4垂直圆管为计算域,在两个切面上设置对称边界条件以模拟整根垂直管,管壁厚度忽略,简化模型如图2。采用ANSYS 中的ICEM CFD 软件对模型划分网格,为了使模拟更容易收敛,垂直管整体采用六面体网格划分,高度方向上网格长度为1 mm,进出口采用Y 形网格划分,壁面处网格适当加密,宽度为0.1 mm,网格总数量45 万。进口处网格分布如图3 所示。
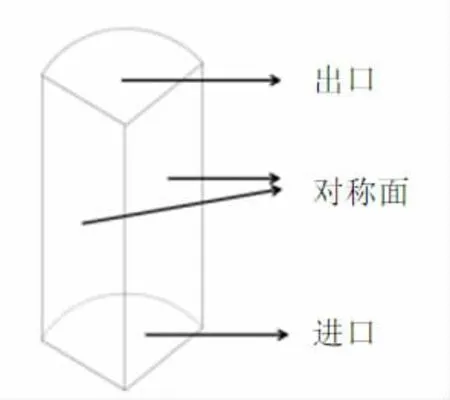
图2 模型简化示意图
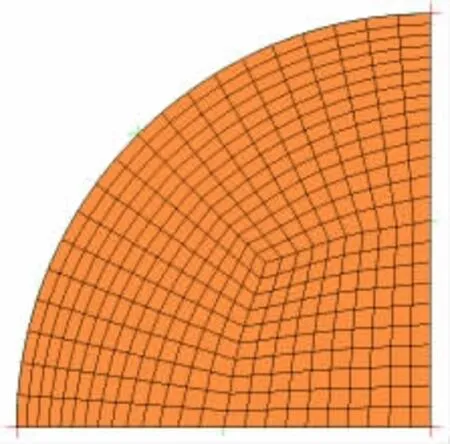
图3 进口处网格划分示意图
管道入口处的质量流量和温度指定为均匀分布,出口设定压力边界条件。考虑到壁面上气泡生成过程中存在滑移现象而不受剪切力作用,而液相在边界层满足无滑移条件。表1 为气泡泵模拟的参数。
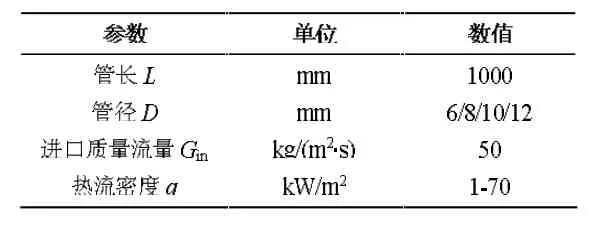
表1 气泡泵模拟的参数
3 模型验证
最终采用以上模型对气泡泵泵内流动沸腾进行模拟分析,为了验证模型的有效性,将利用所建立的模型分别对孙奇[14]和C.C.Bartolemei[15]的实验方案下进行数值模拟,并分别将模拟得到的空泡份额分布结果与文献中的结果进行对比。文献工况如表2 所示,对比结果如图4 所示。
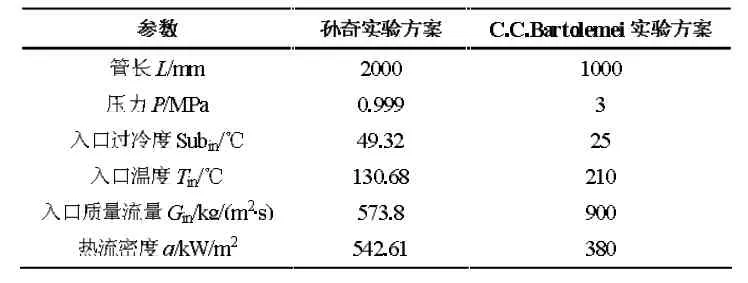
表2 验证工况参数表

图4 与实验结果对比
与孙奇实验结果的对比,选取高度为950 mm 处径向空泡份额。由于是过冷沸腾且过冷度较大,在壁面上的活化核心产生气泡,脱离壁面后的气泡首先在近壁区发生碰撞聚合成较大直径气泡,然后向管中心流体主流区流动过程中冷凝变小,因此截面上汽泡直径的最大值出现在壁面附近,模拟结果和实验结果共同说明了这一现象。模拟结果与实验结果存在一定误差,整体误差在15%,但趋势一致。与C.C.Bartolemei实验结果的对比,选取的是沿高度方向的截面平均空泡份额。相同模拟条件下,空泡份额与实验值变化趋势相同,而且结果比J.C.LAI[16]更加接近实验值。
4 模拟结果与分析
4.1 最佳热流密度
图5 给出了出口质量流量G=40kg/m2s 时出口液相表观速度与热流密度的关系曲线。其中,表观速度并非流体的真实速度,它是指气泡泵壁面由于加热产生大量气泡,管内形成气液两相流,每单位流道截面上的体积流量,是一种经截面权重后的平均速度。
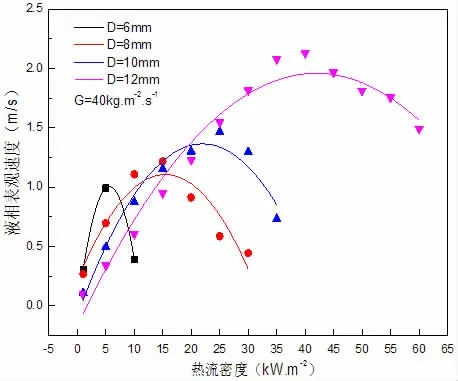
图5 出口处液相表观速度随热流密度大小的变化
出口液相表观速度的大小反映了气泡泵提升能力的大小。液相表观速度越大,表示气泡泵提升能力越强。热流密度越大,壁面上核化点处越容易生成气泡,气泡泵内气泡聚集,空泡份额越大,流态处于弹状流或者搅拌流,此时提升能力最强。当热流密度达到一定值后,管内气泡越来越多,流动越来越不稳定,最终液相被气泡挤压到管壁,存在一层液膜贴附管壁向上流动,流态成为环状流,提升能力会大幅度减弱。所以图5 显示出液相表观速度随着热流密度的增大先增大后减少,存在一个最大值,即存在一个最佳热流密度使得气泡泵的提升能力达到最大。管径越大,由于进口流量相同,管内工质越多,所需加热量越大,所需的最佳热流密度值会更大。
改变进口质量流量,出口液相表观速度随热流密度变化曲线趋势相同,不同管径的气泡泵,在每个质量流量下都存在一个最佳热流密度。将每个质量流量下最佳热流密度绘制在一张图上,如图6,最佳热流密度与管径存在线性关系:


图6 不同进口流量下最佳热流密度随管径的变化
不同的进口流量下拟合直线的斜率和截距不同,求图6 中斜率a 和b,见表3。
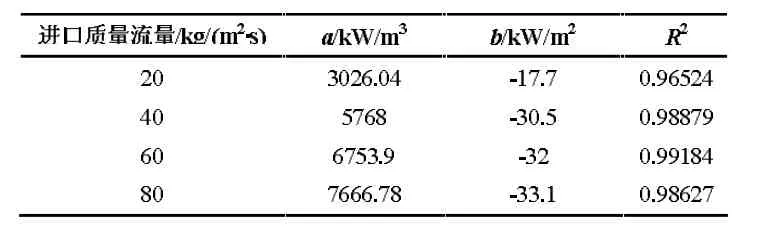
表3 不同进口流量下的拟合值
根据表3 中数据,a 和b 与进口流量G 存在一定关系,将数据进行拟合,如式(6)~(7):

将式(6)和式(7)带入式(5)可得到最佳热流密度与进口质量流量和管径的关系式:

4.2 最小热流密度
所谓最小的热流密度表示气泡泵能够刚好提升液相,即整个制冷循环能够刚好运行时的热流密度值。将不同管径下最佳热流密度随进口质量流量的变化曲线绘制在图7 中。最佳热流密度值与进口质量流量之间存在线性关系。每条直线的截距b0,刚好是液相提升量为零时的值,所对应的热流密度表示最小热流密度值。根据图7 可求不同管径下的拟合直线截距b0,见表4。
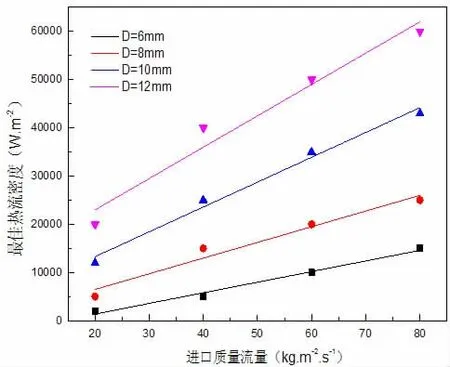
图7 不同管径下最佳热流密度随进口质量流量的变化

表4 不同管径下的拟合值
最终可得最小热流密度与管径的关系式:

5 结论
本文利用两相流理论建立了三维、稳态的气泡泵两流体模型,采用CFX-19 为求解工具,通过已有的实验数据验证了所建立的模型的正确性。以一个大气压下水为工质,模拟研究了气泡泵垂直管内气液两相流动。通过数值计算发现,热流密度大小对于气泡泵运行有重要意义。本文主要研究结论如下:
1)气泡泵出口的液相表观速度随着热流密度的增大先增大后减少,存在一个最佳热流密度。
2)最佳热流密度与入口流量之间存在二次函数关系,与管径之间是一次函数关系。
3)最小热流密度只与管径有关。

