基于PCA-CRHJ模型的矿井突水水源判别

秋兴国，王瑞知，张卫国，张昭昭，张婧

(西安科技大学 计算机技术与科学学院， 陕西 西安 710054)

0 引言

矿井突水灾害事故危害巨大，据中国煤矿安全生产网站统计，2013—2019年我国共发生煤矿水害事故39起，占全国煤矿总事故的11.21%；因煤矿水害导致死亡的有246人，占全国煤矿总事故死亡人数的14.03%[1]。快速判断水源类别并及时确定突水危险发生位置是有效预防突水事故发生及水害治理的重要方法和技术手段。

颜丙乾等[2]通过主成分分析(Principal Component Analysis, PCA)得出不同水样的矿化程度，将马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)引入到贝叶斯(Bayes)方法中，建立了基于PCA和MCMC的Bayes方法的矿井突水水源判别模型。聂凤琴等[3]建立了基于马氏距离的矿井突水水源判别模型，通过划分不同水源间的距离对水源类型进行区分。孙福勋等[4]在Fisher判别分析理论的基础上引入质心距评价法剔除混合水样样本，实验证明改进后的模型判别准确率从60%提高到了83.3%。姜子豪等[5]提出了一种基于Bayes-可拓判别法的矿井突水水源判别方法，避免了Bayes判别法中各特征指标对总体样本的影响及可拓判别法忽视误判损失带来的判别误差问题，可有效提高水源判别精度。杨勇等[6]采用卷积神经网络(Convolutional Neural Networks, CNN)建立矿井突水水源判别模型，实验证明该模型适用于处理多维突水序列。刘东锐等[7]利用遗传算法(Genetic Algorithm,GA)对传统支持向量机(Support Vector Machine, SVM)进行优化，建立了GA-SVM水源判别模型，解决了SVM模型参数选取经验化的问题。李垣志等[8]建立了基于回声状态网络(Echo State Network, ESN)的矿井突水水源判别模型，削弱了人为因素的干扰。以上模型虽然具有一定的实用性，但仍存在非线性能力较差、模型稳定性较差、判别精度低等问题。为此,本文基于PCA和确定性分层跳跃循环网络(Cycle Reservoir with Hierarchical Jumps, CRHJ)构建了PCA-CRHJ模型。将该模型应用于2个实际煤矿的突水水源判别，以验证该模型的实用性和有效性。

1 理论与算法

1.1 PCA

假设原始数据集包括n个数据样本，每个样本具有p个指标Z1—Zp，对此数据集的PCA数据分析计算流程如下。

(1) 对原始数据集进行标准化处理，组成标准化数据矩阵。

(2) 根据Pearson相关系数[9]计算各个变量数据间的相关性，组成相关系数矩阵。

(3) 求解关于相关系数矩阵的特征方程，对求出的特征值λ进行排序(从大到小)，即λ1≥λ2≥…≥λp，并求出每个特征值所对应的单位特征向量L1—Lp，所有单位特征向量组成的主成分得分矩阵为

(1)

式中lpp为单位特征向量Lp的第p个得分系数。

(4) 计算累计贡献βm，保留累计贡献率在85%以上的前m个成分作为新的主成分。

(2)

(5) 原始数据集经过PCA处理后得到重组数据集，第m个新主成分的数学模型Fm为

Fm=l1mZ1+l2mZ2+…+lpmZp

(3)

1.2 CRHJ

确定性循环跳跃网络(Cycle Reservoir with Regular Jumps, CRJ)是一种能够进行时间序列分析的新型递归神经网络[10]，其储备池采用简单的确定型循环拓扑结构，解决了ESN储备池随机连接结构不易受控制的问题。与CRJ拓扑结构不同的是，CRHJ的储备池采用分层跳跃拓扑结构，内部活跃度明显提高，在保证内部多样性的同时增强了内部稳定性，从而增强了模型的非线性能力，使其表现出卓越的性能。

图1 N=12，J=3的CRJ拓扑结构Fig.1 CRJ topological structure with N=12 and J=3

图2 N=18，J1=2，J2=4，J3=8的CRHJ拓扑结构Fig.2 CRHJ topological structure with N=18 and J1=2，J2=4，J3=8

CRHJ的更新公式为[12]

x(t+1)=f(Vs(t+1)+Wx(t)+z(t+1))

(4)

式中：x(t)为t时描述储备池内部状态的状态变量,x(t)=(x1(t),x2(t),…,xN(t))T；f为储备池激活函数，通常取tanh函数或sigmoidal函数；V为输入连接权值矩阵，由输入连接权重r1={-v,v}组成，矩阵大小为N×K；s(t)为t时的输入变量,s(t)=(s1(t),s2(t),…,sK(t))T；W为储备池权值矩阵，由r2和rjk组成，矩阵大小为N×N；z(t)为独立且均匀分布的随机噪声。

y(t+1)=Ux(t+1)

(5)

式中：y(t)为t时的输出变量,y(t)=(y1(t),y2(t),…,yH(t))；U为输出连接权值矩阵，利用Tikhonov正则化方法[13]求出矩阵大小为H×N。

2 模型应用

为了验证基于PCA-CRHJ模型的矿井突水水源判别的实用性和有效性，将该模型应用到安徽淮南张集煤矿和新庄孜煤矿的突水水源判别中。

2.1 数据预处理

采用最大最小归一化方法分别对数据集A、B中的数据进行标准化处理。

利用Pearson相关系数ξ评估标准数据矩阵各个指标变量之间的线性相关程度。取相关程度阈值为0.8，|ξ|>0.8表示2个变量之间线性相关程度较高。数据集A各指标相关系数见表1，数据集B各指标相关系数见表2。表1中，相关系数的绝对值大于0.8的有X1和X8，X2和X8，X4和X6，X4和X11，X6和X11，X7和X11，11对指标中有6对指标相关性过大，信息重叠使得信息丰富性降低。表2中，相关系数的绝对值大于0.8的有Y3和Y4，Y1和Y5，Y1和Y7，Y5和Y7，7对指标中有4对指标相关性过大，信息重叠使得信息丰富性降低。因此，对数据进行PCA分析，突出各个指标的特征，避免对模型精度的影响。进行PCA分析时，计算得到各个主成分的特征值、贡献率、累计贡献率，见表3。

表1 数据集A各指标相关系数Table 1 Each index correlation coefficient in data set A

表2 数据集B各指标相关系数Table 2 Each index correlation coefficient in data set B

表3 数据集A、数据集B各成分特征值、贡献率、累计贡献率Table 3 Characteristic value, contribution rate and cumulative contribution rate of each component in data set A and set B

(6)

(7)

2.2 网络参数的设定

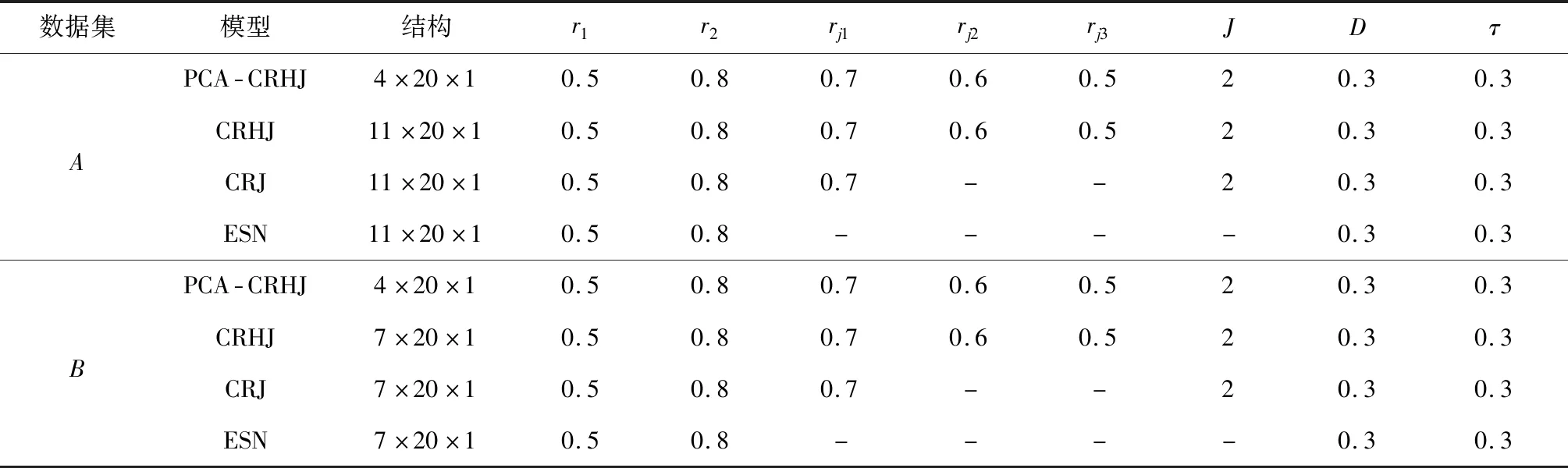
表4 模型参数Table 4 Model parameters

3 结果分析

基于数据集A与数据集B，对PCA-CRHJ、CRHJ、CRJ、ESN模型进行矿井突水水源判别模拟实验。将各个模型分别运行100次。

3.1 误差分析

模拟实验采用均方根误差RMSE对模型的准确率进行评估，当RMSE接近于0时，表示模型准确率高。

基于数据集A的判别误差分布如图3所示，基于数据集B的判别误差分布如图4所示，各模型的判别结果与误差见表5。对比图3和图4可知，由于ESN的输入权值矩阵与储备池的连接权矩阵在每次训练时均需随机生成且网络内部状态不稳定，所以,模型误差分布波动性较大；PCA-CRHJ、CRHJ、CRJ的输入权值矩阵与储备池连接权值矩阵在训练前已确定且保持不变，确定性跳跃循环的拓扑结构使得训练过程中网络内部状态保持稳定，所以,模型误差分布平稳。根据表5计算分析可得：基于数据集A训练的PCA-CRHJ模型的精度比CRHJ模型提高了79.81%，比CRJ模型提高了79.95%，比ESN模型提高了86.55%；基于数据集B训练的PCA-CRHJ模型的精度比CRHJ模型提高了48.95%，比CRJ模型提高了61.43%，比ESN模型提高了61.89%。4种模型模拟准确率高低顺序如下：PCA-CRHJ>CRHJ>CRJ>ESN。由表5中期望输出与判别结果可知，PCA-CRHJ模型的判别结果与期望输出一致，模拟准确率达到了100%。

图3 基于数据集A的误差分布Fig.3 Error distribution of data set A

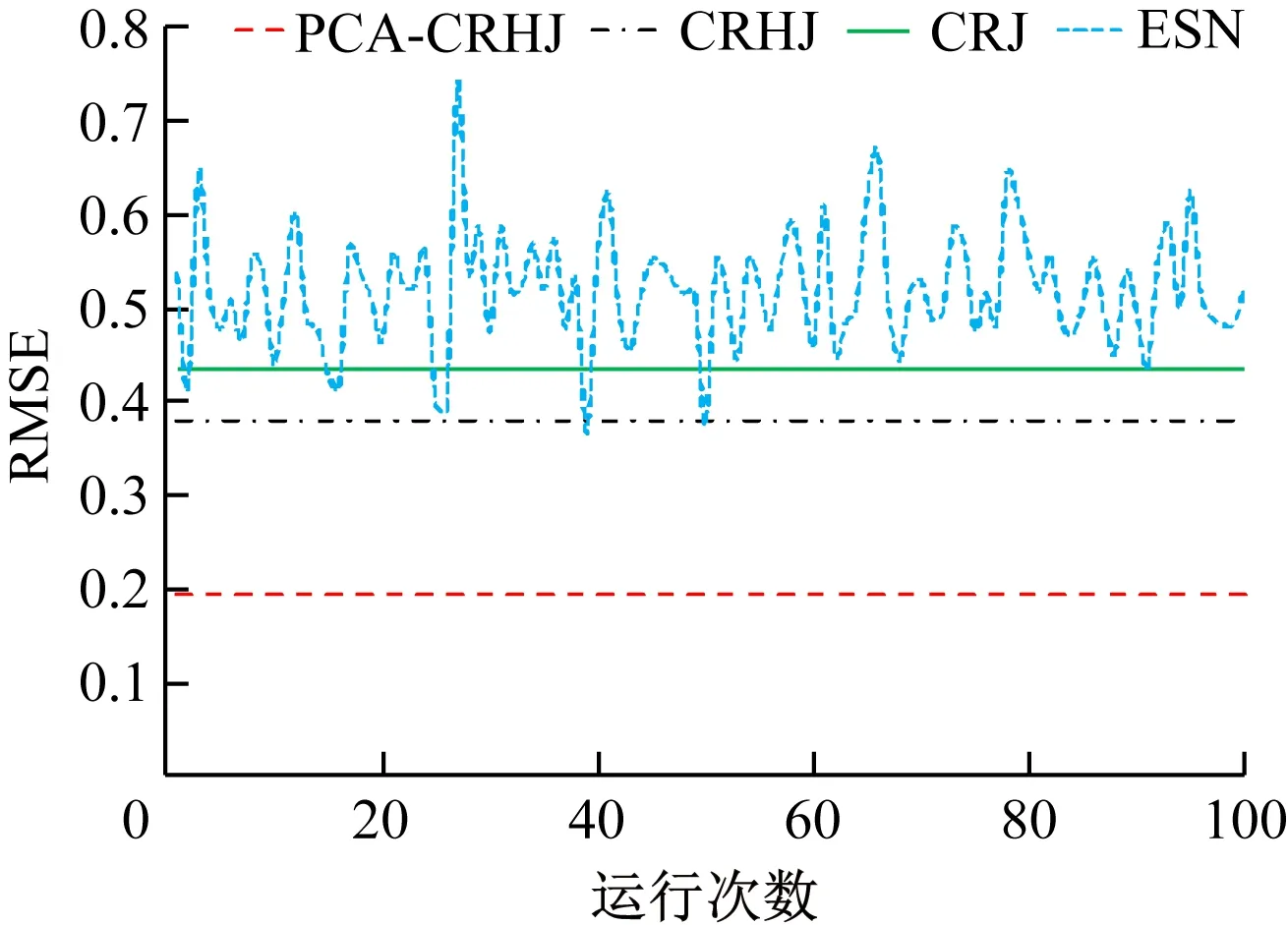
图4 基于数据集B的误差分布Fig.4 Error distribution of data set B

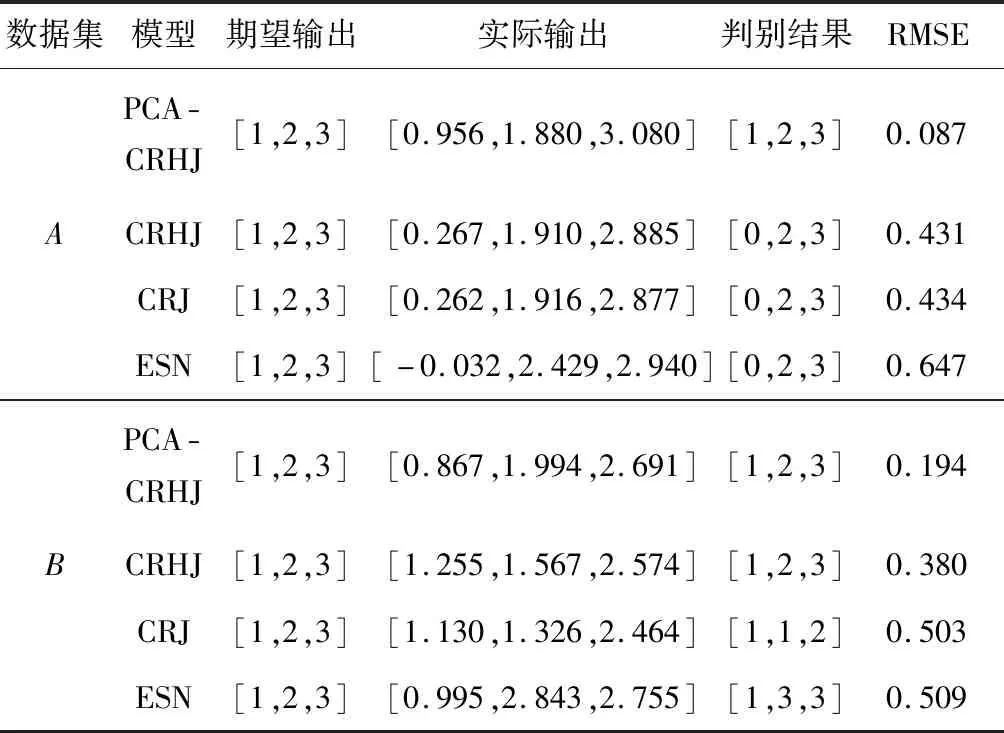
表5 判别结果与误差Table 5 Discrimination results and errors

3.2 参数敏感性分析

PCA-CRHJ模型有5类主要参数，分别为储备池规模N、输入连接权重r1、单向连接权重r2、分层双向跳跃权重rjk、跳跃步长J。

(1) 3类权重参数的敏感度分析。保持N=20和J=2不变，依次改变其余3类权重参数值，以RMSE作为评判指标讨论3类权重参数的敏感性。PCA-CRHJ模型不同权重参数的误差分布如图5所示，其中图5(a)为误差放大前的模拟结果，图5(b)为将误差放大至[0.083,0.090]区间的模拟结果。本文所用PCA-CRHJ模型共有3层跳跃网络，故分层双向跳跃权重依次是rj1，rj2，rj3。从图5(a)可看出，输入连接权重r1对模型模拟结果的影响最大，当其取值在[0,0.4]时，RMSE随着输入连接权重r1的增大而减小，模型模拟结果误差较大，当其取值大于0.4时，RMSE趋于稳定；r2，rj1，rj2，rj3对模型模拟结果影响均较小。从图5(b)可得出，5个权重参数-RMSE曲线的斜率(θ)大小依次是θ1>θj1>θ2>θj3>θj2，因此，5个权重参数对模型误差模拟的影响大小依次为r1>rj1>r2>rj3>rj2。

(a) 误差放大前

(2) 储备池规模及跳跃步长的敏感度分析。设3类权重参数取得最优值且保持不变，跳跃步长取值范围为[2,60]，储备池规模分别取500，400，300，200，100，误差分布如图6所示。从图6横向观察，跳跃步长J对模拟结果的影响整体上趋于平稳，影响较小；纵向观察，当跳跃步长J一定时，不同储备池规模N的取值使RMSE产生较大差异，因此,储备池规模N对模型模拟结果影响较大。其原因主要在于所用水源判别的数据集太小，选用较大的储备池规模N易使模型产生过拟合现象，从而使误差增大。所以,对于PCA-CRHJ网络，当数据集较小时，选用较小的储备池规模N将得到更优的结果。

图6 PCA-CRHJ模型储备池规模参数及跳跃步长参数的误差分布Fig.6 Error distribution of reservoir scale and jump size in PCA-CRHJ model

4 结论

(1) 采用PCA对数据集进行预处理，有效提取多元时间突水序列的数据特征，重构原始数据，结合具有多元时间序列分析能力的CRHJ神经网络建立PCA-CRHJ模型,用于矿井突水水源的判别。通过与CRHJ、CRJ、ESN模型进行对比，表明PCA-CRHJ模型的实际判别效果最优，准确率可达100%。

(2) 对PCA-CRHJ模型参数敏感性进行分析，表明输入连接权重参数对模型判别结果的影响最大，5个权重参数对模型模拟结果影响大小的顺序依次是r1>rj1>r2>rj3>rj2；当3类权重参数取得最优值且保持不变时，储备池规模对模型误差影响最大，而跳跃步长的影响则较小。